Задача
На плоскости проведены n прямых, разбивающих ее на области. Они раскрашиваются в шахматном порядке: области, имеющие общие стороны, должны быть покрашены в разные цвета. Чему равна максимальная разность между числом черных и белых областей?
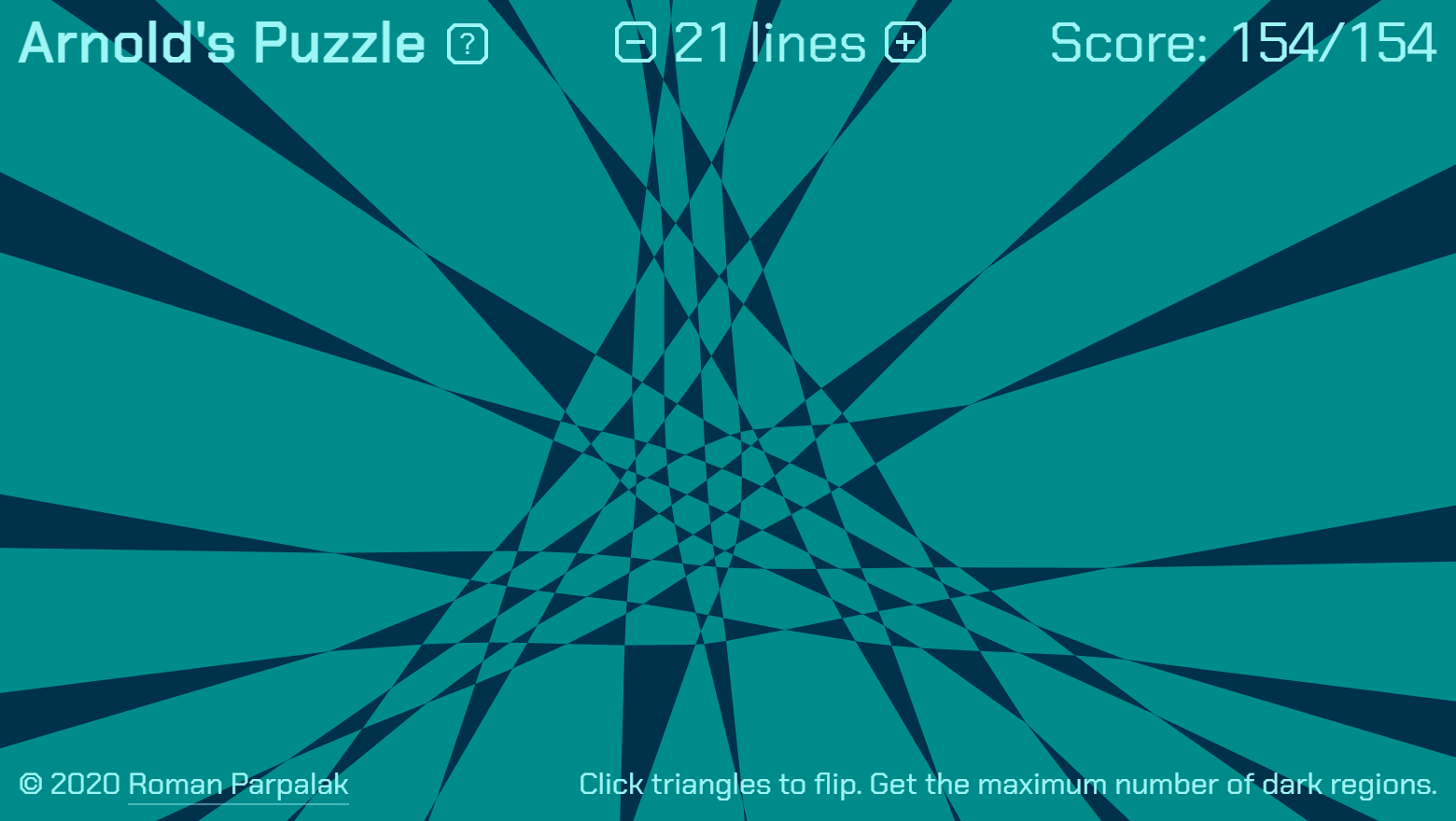
PS. Для заинтересовавшихся этой задачей приведу одну картинку для семи прямых:
Разность между числом черных и белых областей на этом рисунке — 7. Расположение прямых, дающее такую разность, не единственное, но вычисления на компьютере показали, что улучшить данный результат нельзя.
9 марта 2008 года, 20:44 математика · задача Арнольда
Комментарии
А когда плоскость разбивается прямыми, можно доказать, что двух цветов достаточно.
Есть интуитивное подозрение, что максимальная разница — 1, как формально доказать пока не знаю.
Я добавил к записи для примера картинку, получающуюся для 7 прямых. Там разность — 7.
Некоторые из участников математической олимпиады являются друзьями. Если один участник является другом второго, то второй является другом первого. Назовем группу участников компанией, если любые двое из них друзья. (В частности, любая группа менее, чем из двух участников, является компанией.) Количество членов компании назовем ее размером.
Известно, что в данной олимпиаде наибольший размер компании является четным числом. Доказать, что участников можно разместить в двух комнатах так, что наибольший размер компании, находящейся в одной комнате, равен наибольшему размеру компании, находящейся в другой комнате.
Оставьте свой комментарий