задача Арнольда
Головоломка Арнольда ★
Постоянные читатели помнят, что мы с коллегами по учебе лет 10 назад занимались задачей Арнольда. В ней остались открытые вопросы, и я недавно решил к ним вернуться. Дописал одну из программ, отрисовывающих и распрямляющих конфигурации, и понял, что получилась хорошая игровая механика для головоломки. Переписал код визуализации и моделирования на js, и получилась браузерная головоломка.
Правила
В этой игре выполняются простые правила:
- На плоскости проведены несколько линий, каждая пара линий пересекается в одной точке.
- Линии разбивают плоскость на области, раскрашенные в шахматном порядке.
- Вы можете перестраивать разбиение, «схлопывая» и «выворачивая» треугольники.
- Ваша цель — получить максимально возможное количество темных областей.
В простейшем случае 5 линий процесс игры выглядит так:

Пользовательский опыт
При небольшом количестве линий решить головоломку можно случайным перебором. Нужно помнить, что иногда надо «пожертвовать» счетом (количеством темных областей), так как не всегда есть «прямая дорога» к цели, на которой счет только увеличивается.
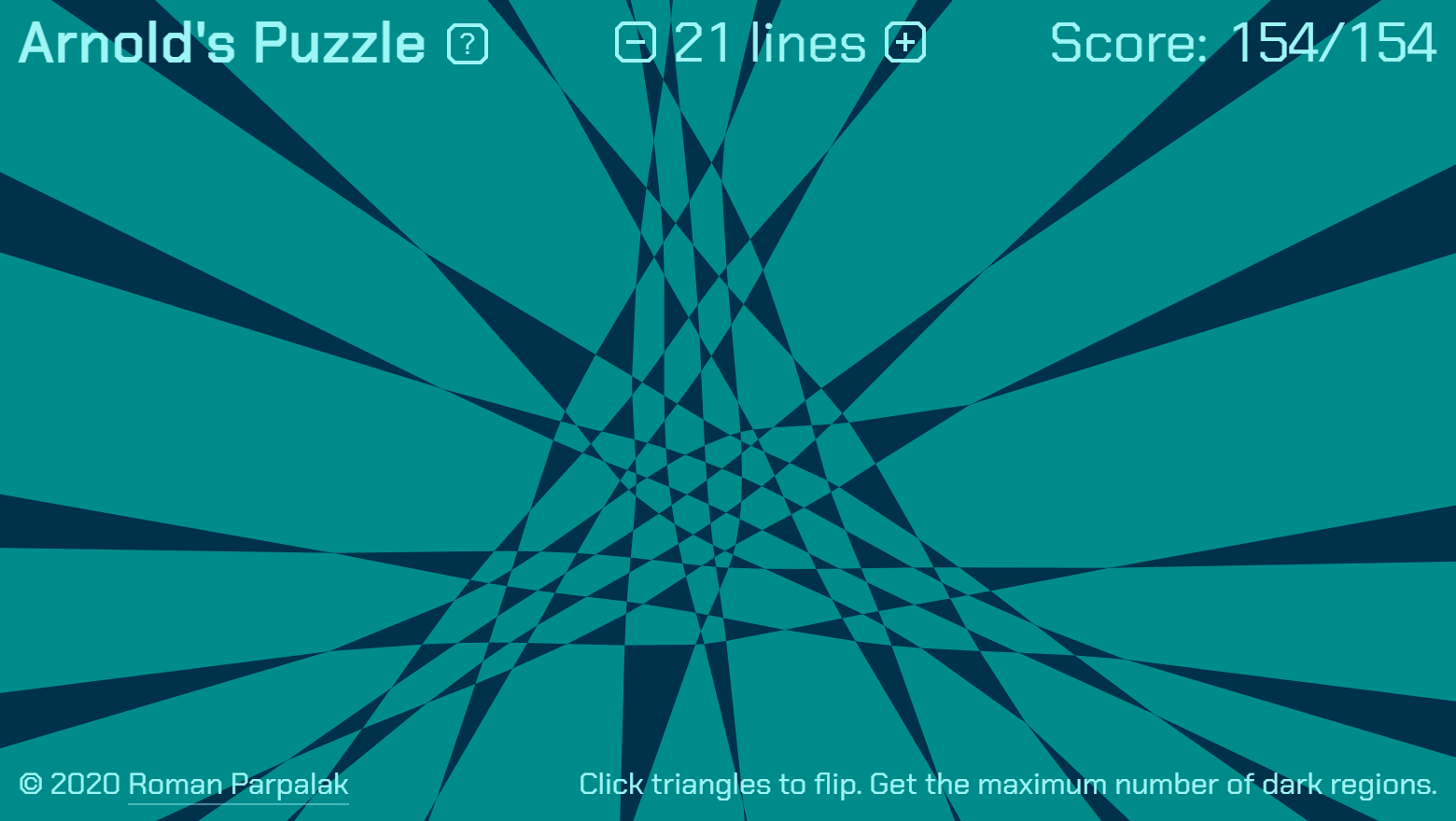
Я довольно быстро «прошел» все уровни до 19 линий. 21 линию (на скриншоте в начале) собрал часа за полтора. Правда, я знал, что существует
С увеличением уровня сложность игры растет не только количественно (нужно дольше идти к цели), но и качественно: приходится придумывать новые приемы и подходы, так как старых становится недостаточно.
По ощущениям игра похожа на паззл, каждый кусочек которого подходит к любому другому кусочку, но общая картина из них всё никак не складывается.
Игра полностью отвлекает от происходящего вокруг, подходит для убивания времени в метро.
Математическая основа
Напомню формулировку задачи Арнольда:
На плоскости проведены N прямых. Найти максимальную разность между числом черных и белых областей шахматной раскраски дополнения.
Это открытая математическая проблема. Она является частным случаем
Таким образом, переворачивая треугольники в головоломке, вы на самом деле решаете в частном случае
Для преобразования конфигураций в головоломке именно схлопывание треугольников выбрано не случайно. Оказывается, с помощью таких схлопываний можно перевести произвольную конфигурацию в любую другую конфигурацию. Действительно, линии на плоскости, описанные в правилах, называются конфигурацией (псевдо)прямых. Они представляют элемент из группы кос. Суть теоремы Артина об образующих группы кос как раз и состоит в возможности перевода конфигураций друг в друга последовательностью преобразований треугольников.
Также задача Арнольда тесно связана с задачей о треугольниках Кобона.
Вместе со мной Денис Уткин и Сергей Белёв потратили немало времени на попытки решения, результаты которого есть во многостраничном
Вычислительная модель игры
В основе визуализации — математическое моделирование некоторой «механической» системы. В этой системе массивные точки соединены ломаными линиями, отталкиваются друг от друга, испытывают сопротивление среды. В узлах ломаных — распрямляющие «пружинки». Концы ломаных прибиты внешними зафиксированными точками. Для расчетов движения точек по законам механики применяется метод Рунге — Кутты четвертого порядка с оценкой ошибок и плавающим шагом. Преподаватели вычматов были бы довольны :) Код, как обычно, открыт на гитхабе.
Намайнили
За попытку намайнить биткоины на суперкомпьютере в ядерном центре в Сарове оштрафовали на 450 тысяч рублей. Неплохо так намайнили.
Эх, не тем делом мы занимались на вычислительном кластере ОИЯИ. На 20 ядрах запускали перебор конфигураций в задаче Арнольда, потратили на него десятки тысяч часов процессорного времени. А можно было биткоины майнить.
Исследование на миллион
Задача о расположении прямых на плоскости была сформулирована В. И. Арнольдом в 1983 году. С тех пор эта нерешенная математическая проблема занимает лучшие умы человечества, подкупая простотой формулировки и создавая ощущение (в
Мы с Сергеем Белёвым и Денисом Уткиным рады сообщить о нашем скромном вкладе и представить отчет (PDF, 714 Кб) об упорных двухлетних исследованиях. В них использовались параллельные вычисления на десятках процессоров, некоторые сведения из теории группы кос и симметрической группы, а также факты из школьной геометрии и тригонометрии.
По понятным причинам в отчет включены только наиболее важные результаты. Тем не менее, он содержит изложение нескольких гениальных идей, проливающих свет на отдельные аспекты проблемы, существенно продвигающих ее понимание и даже позволяющих решить задачу в некоторых частных случаях.
Мы надеемся в ближайшем будущем полностью решить задачу и завершить наше исследование.
Летние школы
В ОИЯИ проходила школа по физике высоких энергий. На ней были лекции и доклады. Некоторые были интересными. Некоторые — слишком специфичными и скучными.
Один из лекторов — Андрей Грозин — ходил в прикольной футболке с надписью «посторонись, несу ахинею».

Впрочем, стоит заметить, что говорил он умные и дельные вещи.
В программе школы были предусмотрены развлекательные мероприятия: в один из дней мы катались по Волге и ели шашлыки на открытом воздухе.
А еще я умудрился встретиться с Владимиром Игоревичем Арнольдом (по поводу задачи о прямых). Он читал лекции на летней математической школе в Ратмино, недалеко от Дубны. Там мы его и нашли.
В целом, июльская поездка в Дубну была полезной и продуктивной.
Задача
На плоскости проведены n прямых, разбивающих ее на области. Они раскрашиваются в шахматном порядке: области, имеющие общие стороны, должны быть покрашены в разные цвета. Чему равна максимальная разность между числом черных и белых областей?
PS. Для заинтересовавшихся этой задачей приведу одну картинку для семи прямых:

Разность между числом черных и белых областей на этом рисунке — 7. Расположение прямых, дающее такую разность, не единственное, но вычисления на компьютере показали, что улучшить данный результат нельзя.