О схеме URL сервиса генерации картинок с формулами
В посте про объемный чертеж я привел саму картинку, но не ее код. А без кода картинка бесполезна: нельзя ни подсмотреть, как она сделана, ни изменить под свои нужды.
На самом деле код картинки содержится в ее адресе. Как писал Якоб Нильсен 19 лет назад, URL — это интерфейс. И я принял такое интерфейсное решение. Формула на латехе (например, a^2+b^2=c^2) кодируется и добавляется в урл:
//i.upmath.me/svg/a%5E2%2Bb%5E2%3Dc%5E2По нему открывается сама картинка с формулой: $$a^2+b^2=c^2$$.
Таким образом, из адреса картинки расшифровкой можно получить ее исходный код. Чтобы облегчить этот процесс, я сделал адрес другого вида (от svg остается последний символ):
//i.upmath.me/g/a%5E2%2Bb%5E2%3Dc%5E2По этой ссылке открывается
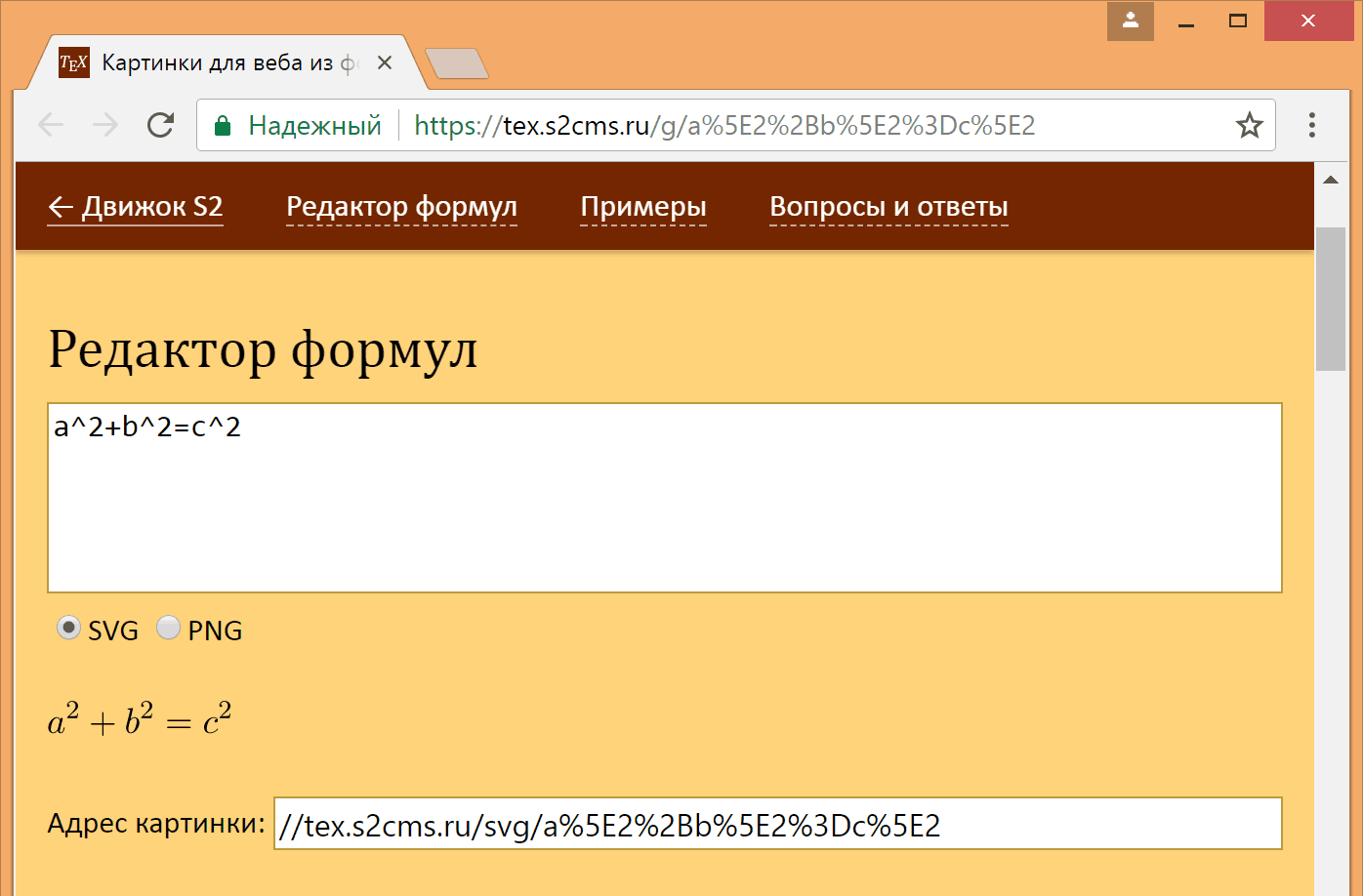
Вообще, исходный код может быть достаточно длинным. Вот пример, в котором на комплексной плоскости отмечены первые 10 степеней числа $$1+i\pi/10$$:
\begin{tikzpicture}[scale=1.0545]\small
\tikzset{>=stealth}
\def\k{10}
\def\p{3.1415926/\k}
\def\r{3.1}
\def\l{5.8}
\def\t{0.07}
\draw[->,thin,gray] (-\l,0)--(\l,0);
\draw[->,thin,gray] (0,-0.6)--(0,\l);
\draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$};
\foreach \l in {1,...,\k}
\draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)});
\draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}) node[pos=0.91,above] {$-1,\!5934+0,\!1561i$};
\draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$}
(-\r,\t)--(-\r,-\t) node[below]{$-1$}
(\t,\r)--(-\t,\r) node[left]{$1$}
(0,0) node [anchor=north west,yshift=-0.07cm] {$0$};
\draw [line width=0.21mm,opacity=0] (-\l,-0.6) rectangle (\l,\l);
\end{tikzpicture}Результат:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{10} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}) node[pos=0.91,above] {$-1,\!5934+0,\!1561i$}; \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.2mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
Этот пример я взял из статьи о формуле Эйлера $$e^{i\pi}=-1$$. Первую версию картинки рисовал вручную. В Maple выполнил возведение в степень и построил график. Открыл его в фотошопе и поверх дорисовал
На версию с графиком в tikz ушло столько же времени, или даже больше. Но масштабируемость результата находится на совершенно другом уровне. Чтобы нарисовать первым способом вдвое больше векторов, нужно потратить вдвое больше времени. Второй способ требует изменения одного числа k в исходном коде, и foreach сделает всю работу. Вот 20 векторов:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{20} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}); \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.2mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
Вот 50:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{50} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}); \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.2mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
URL последней картинки длиной 1192 символа. В принципе, такие длинные адреса не очень красивы. Но и большой проблемы в этом нет. В стандарте нет ограничений на длину URL, да и с практическим ограничением в браузере или
Меня просили изменить алгоритм кодирования, чтобы укоротить адреса.
Необходимости в этом я пока не вижу. Но если буду делать доработку, то поступлю аналогично. Адрес /svgb/... с закодированными в /gb/... на дешифрованный вариант в редакторе формул.



Оставьте свой комментарий