Чему же равно 6:2(1+2)?

Когда я впервые увидел этот пример в интернете, подумал, что это проблема на ровном месте. Да, мнения людей об ответе расходятся: кто-то отвечает 1, а кто-то 9. Но в реальности никакой путаницы не бывает, хотя бы потому, что деление обозначается двоеточием разве что в школе. В книгах и статьях формулы с делением записываются в виде дроби, и сначала нужно выполнить действия в числителе (над чертой) и в знаменателе (под чертой), и только потом выполнять деление, обозначаемое чертой. С такой записью разночтений нет:

$${6\over 2(1+2)}={6\over 6}=1.$$

Борис Трушин смог снять по этой теме целых два видео по 18 минут:

После просмотра я сделал для себя такой вывод. Приоритет арифметических действий учат в начальной школе, а опускать знак умножения — только в средней школе. По характеру необходимых действий пример 6:2(1+2) — из начальной школы, поэтому он записан некорректно, умножение между двойкой и скобками опускать нельзя.

И совсем недавно мне попалось еще одно видео по теме. Оказывается, мнение о правильном ответе расходятся не только у спорящих в интернете, но и у производителей калькуляторов!

В этом видео отметил следующие вещи. Оказывается, около 100 лет назад еще были колебания в определении приоритета (явного) умножения и деления, но колебания приоритета неявного умножения над делением не было: если знак умножения опущен, выражение воспринимается единым целым, будто записано в скобках. К девяностым годам североамериканские учителя повлияли на производителей калькуляторов, чтобы те изменили приоритет неявного умножения и выровняли его с явным умножением и делением. Но так сделали не все производители, а сейчас происходит частичный откат к тому, что неявное произведение становится приоритетнее. Колебания приоритета неявного умножения относятся только обучению в школе, в профессиональном употреблении колебаний нет.

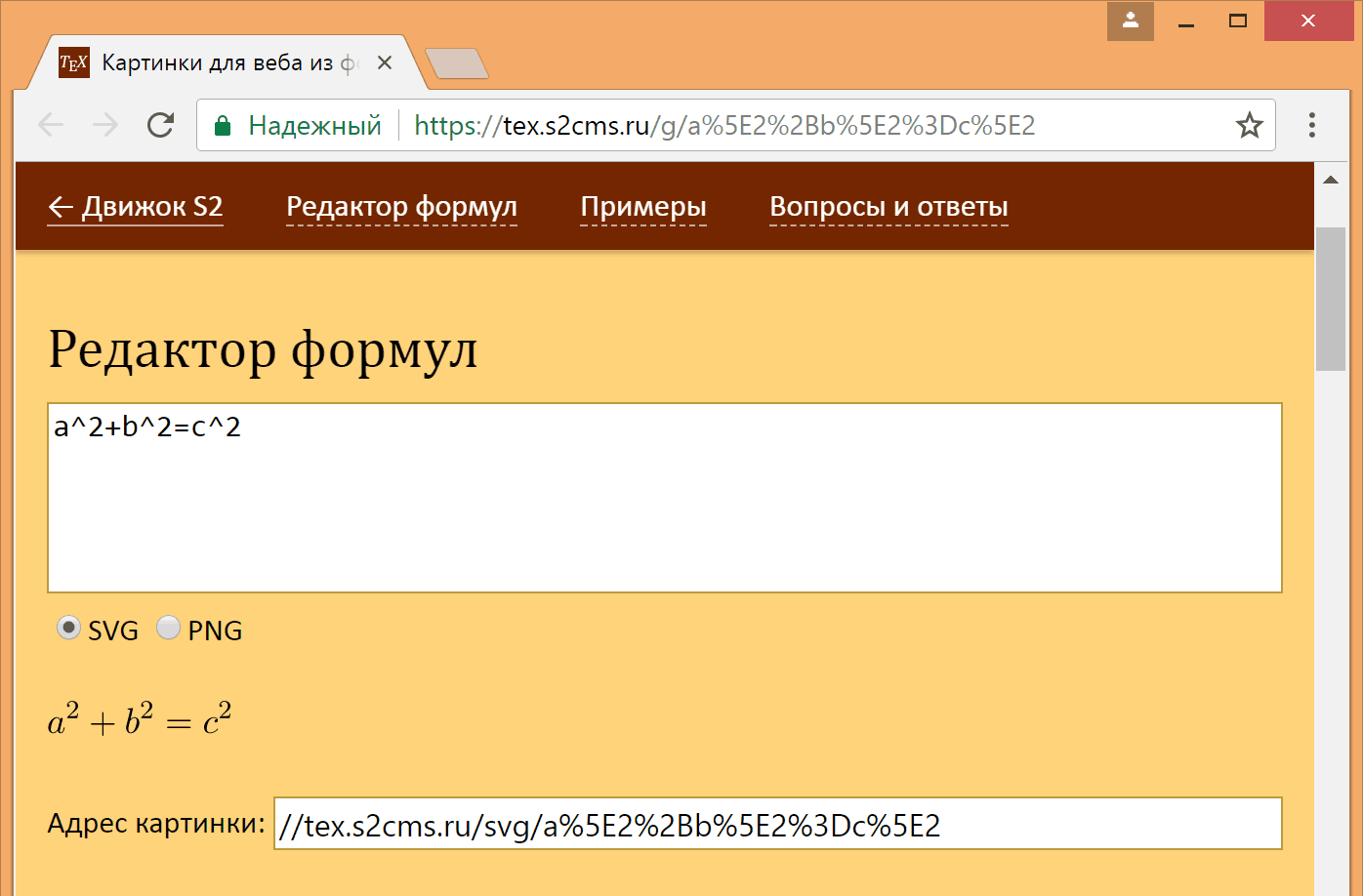
После просмотра этого видео я понял, что мой аргумент про использование двоеточия как знака деления в основном в начальной школе — это всего лишь отрицание проблемы. Действительно, использование горизонтальной черты для обозначения деления удобно в отдельных формулах, а не в сплошном тексте. Сейчас в математических текстах вместо двоеточия используется наклонная черта. Так что никто не мешает спросить, чему равно 6/2(1+2).

Я решил посмотреть, как сам записывал в одну строку формулы с делением и неявным умножением, и какие приоритеты подразумевал. Прошелся по текстам в блоге о теоретической физике старше нескольких лет, чтобы исключить возможное влияние обсуждений этого вирусного примера. В выражении (5/4) v/R взял в скобки числовой множитель, чтобы показать, что получившаяся величина на четверть больше некоторой характерной угловой скорости v/R. При этом (5/4) v/R ≠ 5/4v/R = 5/4vR. По тем же соображениям использовал скобки в (4π/c) j, здесь так же (4π/c) j = 4πj/c ≠ 4π/cj. В выражении v/(pR) оставил в знаменателе скобки для понятности, их можно было бы убрать. И, наконец, c²/4G. Здесь и 4, и G в знаменателе, c²/4G ≠ c²G/4. Получается, я вполне последовательно использовал неявное умножение с более высоким приоритетом, чем деление, хотя и не могу вспомнить, что подобному правилу нас учили так же, как, например, формуле для решения квадратного уравнения.

Раз уж мы обсуждаем приоритеты арифметических действий, поделюсь воспоминанием из начальной школы, кажется, из второго класса. Учительница нам говорила, что если в выражении на одном уровне несколько умножений и делений, то выполняются сначала деления, а потом умножения. Такого правила я больше нигде не встречал. Обычно учат, что умножение и деление выполняется подряд, слева направо. Например, 8/4×10/2 = 2×10/2 = 20/2 = 10. Если воспользоваться «странным» правилом о приоритете деления над умножением, тоже получится 8/4×10/2 = 2×5 = 10. При этом нельзя, например, сначала выполнить все умножения, а потом все деления. В нашем примере получилось бы 8/(4×10)/2 = 8/40/2 = 0,1, что не совпадает с правильным ответом. Как вы думаете, всегда ли «странное» правило приоритета деления над умножением приводит к тем же результатам, что и обычное правило? Или сможете найти контрпример?