Удивительный мир квантовой механики

Мы с Кириллом Борисовым побеседовали о квантовой механике, о ее необычных особенностях и об устройстве микромира. В своем рассказе я старался не выходить за рамки школьной программы. Читайте переработанную и иллюстрированную расшифровку нашей беседы.

Можно ли понять квантовую механику?

Ведущий: Меня поражает та степень непонятности и удивительности, которая есть в квантовой механике. Для меня это совершенно непостижимые вещи, которые увлекают, которые заставляют задуматься о том, что тот мир, который мы все познаем на опыте, интуитивный мир, он не единственный. То есть есть еще какой-то мир, о котором я тебе предлагаю рассказать.

Гость: Надо признать, что, пожалуй, никто на самом деле не понимает квантовую механику. Возможно, к ней можно только привыкнуть. Но здесь возникает интересный вопрос: что такое понимание вообще? Можно ли считать, что понимание — это просто привыкание? То есть, если нам кажется, что мы что-то понимаем, может быть мы всего лишь привыкли к этому?

Ведущий: Получается, если через 50 лет мы так и не поймем, что такое квантовая механика, но привыкнем к ней, то можно будет сказать, что мы ее поняли? Привыкание, наверное, проявляется в том, что мы начинаем учитывать что-то в нашей жизни. Когда мы вспоминаем об этом, будь то ученые или обычные люди, мы держим это в уме. Наверное, это и есть привыкание.

Гость: Квантовой механике и так почти 100 лет, вряд ли еще через 50 лет мы поймем о ней что-то новое. Я имел в виду другое. Квантовая механика действительно противоречит нашему повседневному опыту. Но когда будущий ученый начинает изучать квантовую механику, он знакомится с математической формулировкой теории, с описанием различных экспериментов и их результатов. Постепенно он привыкает к этим понятиям и результатам. Трудно сказать, когда именно заканчивается привыкание и начинается понимание.

К обычному поведению объектов, которое описывается классической механикой, все привыкли, и поэтому считают, что понимают это поведение. Возьмем, к примеру, инерцию. Чтобы изменить скорость тела, к нему нужно приложить силу, а если не прикладывать, тело будет двигаться по прямой с постоянной скоростью. Например, водитель нажимает на газ, чтобы разогнать автомобиль, и на тормоз, чтобы остановиться. Вроде бы «понятное» поведение. Но долгое время, начиная от Аристотеля, считалось, что тела не стремятся сохранить свою скорость, а останавливаются «сами по себе». В давних представлениях о мире не было силы трения. И только опыты Галилея показали, что реальность другая.

Что такое квантовая механика?

Ведущий: Честно говоря, эта тема меня всегда восхищала. Давай начнем с самого начала: расскажи, что такое квантовая механика? Что обычно подразумевают под этими необычными словами?

Гость: Квантовая механика описывает поведение микроскопических объектов, таких как атомы, молекулы и другие элементы микромира. Она отличается от привычной нам классической механики тем, что у микрообъектов, например, электронов, есть свойства, которые не объясняются законами обычной физики. Например, электрон может одновременно находиться в нескольких местах или пройти по двум путям сразу.

Двухщелевой эксперимент

Ведущий: Можно ли считать, что когда электрон проходит по нескольким путям, это и есть то самое состояние суперпозиции?

Гость: Да, именно. Наиболее ярко суперпозиция проявляется в двухщелевом эксперименте — классическом мысленном эксперименте в квантовой механике. Вот как он устроен: берется источник электронов, который направляет их к экрану с двумя щелями. За этим экраном ставится еще один, на котором проецируется картина ударов электронов.

$$\tikzset{every picture/.style={line width=0.8pt}} \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1,font=\sffamily] \draw (130,80) -- (130,140) ; \draw (130,150) -- (130,180) ; \draw (130,190) -- (130,250) ; \draw[blue,domain=0:170, smooth, variable=\y, samples=100] plot ({215-25*sin(0.167*\y r)}, 80+\y); \draw (190,80) -- (190,250) ; \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165.5) -- (130,185) -- (190,165) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,164.5) -- (130,145) -- (190,165) ; \draw (40,175) node [anchor=north][inner sep=5pt] {\shortstack[l]{Источник\\\rule[-0.1mm]{0pt}{2.5mm}электронов}}; \draw (295,185) node [blue] {\shortstack{Интенсивность}}; \end{tikzpicture} $$

В техническом плане экраном может быть фотопластинка, на которой в полной темноте фиксируются следы попадания электронов. Те точки фотопластинки, в которые попали электроны, изменяют свой цвет. После проявки на пластинке остается узор из чередующихся темных и светлых полос.

Ведущий: То есть, у нас есть некая «пушка», стреляющая электронами?

Гость: Да, «электронная пушка» — хороший термин, который используется, например, в кинескопах. Эта пушка стреляет в сторону щелей, часть электронов проходит через нее, часть задерживается и рассеивается по сторонам.

Ведущий: Значит, щель «отбирает» часть электронов из потока?

Гость: Да, это поток электронов, а не один электрон. Если бы через систему прошел только один электрон, мы бы почти ничего не увидели, разве что маленькую светлую точку на фотопластинке.

Ведущий: Мы стреляем пучком электронов через щель в стене. И дальше, за этой стеной, на проекционном экране у нас стоит фотопластина, которая фиксирует проходящие электроны. Что происходит дальше?

Гость: Если щель только одна, напротив нее на фотопластине будет область с большим количеством светлых точек, куда попадают электроны.

$$\tikzset{every picture/.style={line width=0.8pt}} \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1,font=\sffamily] \draw (130,80) -- (130,160) ; \draw (130,170) -- (130,250) ; \draw[blue,domain=-85:85, smooth, variable=\y, samples=100] plot ({200+4000*(sin(-\y*7)/\y)^2}, 165+\y); \draw (190,80) -- (190,250) ; \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165) -- (130,165) -- (190,165) ; \draw (40,175) node [anchor=north][inner sep=5pt] {\shortstack[l]{Источник\\\rule[-0.1mm]{0pt}{2.5mm}электронов}}; \draw (295,185) node [blue] {\shortstack{Интенсивность}}; \end{tikzpicture} $$

Ведущий: Что такое «светлые точки»?

Гость: Это следы попадания электронов на пластинку, в них чувствительный материал фотопластинки меняет свой цвет.

Ведущий: Похоже на ситуацию, когда мы освещаем стену фонариком через отверстие. За стеной мы видим световой след на второй стене. В этом эксперименте будет то же самое? Просто точка света или несколько разбросанных точек?

Гость: Если светить обычным фонариком через обычное отверстие в стене, мы увидим за ним обычный «зайчик», пятно света. Оно состоит из невообразимого количества тех самых «светлых точек», которые сливаются вместе. У этого пятна размытые края, потому что фонарик — не точечный источник света. Заменим теперь фонарик точечным источником, у которого свет исходит практически из одной точки.

Ведущий: Как лазер?

Гость: Можем взять лазер. У него практически нулевая расходимость луча и строго определенная длина волны. Если таким пучком осветить щель, то на экране будет наблюдаться уже не отдельное пятно, а некоторая дифракционная картина, которая возникает из-за того, что свет, проходя около края щели, отклоняется от прямого распространения. Примерно так же, как и волны на поверхности воды могут огибать небольшие препятствия.

Ведущий: То есть, если я плыву в море, я не смогу остановить волну, но при этом она как-то изменит направление из-за меня.

Гость: Верно. Если мы используем в эксперименте не одну щель, а две, то на экране увидим чередующиеся полосы — интерференционную картину.

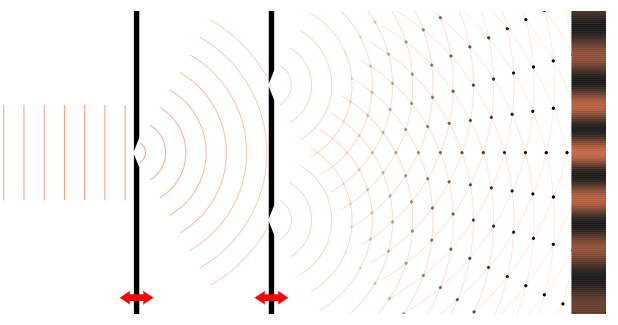
Ведущий: Интерференционная картина — это что-то вроде зебры?

Гость: Да, совершенно верно. Это чередование светлых и темных полос.

Ведущий: То есть получается, что лучи света или электроны распределяются по всей пластине и как-то образуют интерференционную картину? Почему это происходит?

Гость: Чтобы понять, почему возникает эта интерференционная картина, нужно вспомнить, что свет — это волна. Волны от двух щелей могут приходить либо в фазе, либо в противофазе. Когда они приходят в фазе, то усиливают друг друга — в одной точке встречаются два «горба» волн.

Ведущий: То есть, проще говоря, они совпадают?

Гость: Да, они совпадают. Но если мы немного отойдем в сторону, в соседние точки, там одна волна может прийти в фазе, а другая — в противофазе. Тогда «горб» одной волны будет совпадать с «впадиной» другой, и они взаимно уничтожат друг друга.

Ведущий: От чего зависит, совпадут они или нет?

Гость: Это зависит от разности расстояний, которые проходят волны от каждой щели. Условие максимума (светлых полос) состоит в том, чтобы на этих расстояниях укладывалось одинаковое количество длин волн. Кстати, благодаря этому эксперименту можно измерить длину световой волны, а зная скорость света, еще и частоту. Длина просто вычисляется из расстояния между щелями и угла между направлениями на соседние максимумы.

Волны или «шарики»?

Ведущий: Хорошо. Мы выяснили, как ведет себя свет, проходящий через стену с щелями и проецирующийся на экран. Получается интерференционная картина — полосы света и тени. Это понятно на бытовом уровне из аналогии с волнами на поверхности воды. Когда мы пропускаем свет лазера через две щели… Или наверно два лазера можно взять?

Гость: Лучше взять лазер и его отражение в зеркале. Этот опыт может провести каждый: взять лазерную указку, выкрутить линзу из нее. За ней будет лазерный диод — хорошее приближение точечного источника света. Поместив его на зеркало и направив на противоположную стену в затемненной комнате, можно увидеть чередующиеся светлые и темные полосы.

Ведущий: Получается, что каждый может повторить этот эксперимент дома?

Гость: Да, только нужно проявить аккуратность, подобрать ровное зеркало. Возможно, проще будет поэкспериментировать с двумя щелями, например, прорезанными в алюминиевой фольге двумя соприкасающимися лезвиями.

Ведущий: А в чём сложность, когда мы переходим от света к элементарным частицам? Почему картина резко меняется? В чем подвох?

Гость: Подвох в том, что интерференционная картина характерна именно для волн. Такую картину можно наблюдать и для звуковых волн, и на поверхности воды. Но для частиц это поведение нехарактерно. Если пропускать частицы не через одно отверстие, а через два, то, казалось бы, их распределение должно просто складываться. Интерференции быть не должно.

$$\tikzset{every picture/.style={line width=0.8pt}} \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1,font=\sffamily] \draw (130,80) -- (130,144) ; \draw (130,154) -- (130,176) ; \draw (130,186) -- (130,250) ; \draw[dashed,blue,domain=-85:85, smooth, variable=\y, samples=100] plot ({200+4000*(sin(-(\y-25)*7)/(\y-25))^2+4000*(sin(-(\y+25)*7)/(\y+25))^2}, 165+\y); \draw (190,80) -- (190,250) ; \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165.5) -- (130,181) -- (190,190) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,164.5) -- (130,149) -- (190,140) ; \draw (40,175) node [anchor=north][inner sep=5pt] {\shortstack[l]{Источник\\\rule[-0.1mm]{0pt}{2.5mm}электронов}}; \draw (305,215) node [blue] {\shortstack[l]{Ожидаемая \\{\rule[-0.1mm]{0pt}{2mm}}интенсивность \\{\rule[-0.1mm]{0pt}{2.5mm}}для частиц}}; \end{tikzpicture} $$

Однако, когда мы используем электроны и экран с двумя щелями, на фотопластинке возникает такая же интерференционная картина, как от электромагнитных волн.

Ведущий: То есть, важно понимать, что элементарные частицы, как электроны или атомы, не совсем такие материальные, как люди привыкли думать. Это не объекты, которые можно было бы потрогать, если бы мы были достаточно маленькими.

Гость: Да, и это связано с понятием корпускулярно-волнового дуализма. Оно состоит в том, что частицы проявляют волновые свойства, а волны, как свет, обладают признаками частиц, например, «распадаются» на фотоны.

Ведущий: Но ведь световая волна тоже состоит из частиц, из тех же самых фотонов, правильно?

Гость: Верно, из фотонов.

Ведущий: Почему тогда она ведет себя как волна, а один фотон — уже нет? Хотя он по-прежнему остается волной. Здесь и возникает вопрос: как это возможно? Он вроде и «шарик», привычный нам, но…

Гость: Да, когда фотон попадает на фотопластинку, он проявляется как точка, одно зерно чернеет, так что можно сказать, он ведет себя как «шарик».

Ведущий: То есть, когда он взаимодействует с чем-то, он «шарик». Но в пространстве он ведет себя иначе.

Гость: Да, при распространении он проявляет другие свойства.

Ведущий: Хорошо, давай разберемся с этим. Это ведь противоречит обычному опыту на 100%. Можем ли мы найти какие-то аналогии в жизни?

Гость: Я не могу предложить такие аналогии, в этом и сложность квантовой механики. Я хочу отметить, что волновая картина возникает не из-за взаимодействия электронов в пучке, как может показаться. Она присуща каждой отдельной частице. Если ослабить набором полупроницаемых пластин поток фотонов или электронов настолько, что в среднем, например, проходит всего одна частица в секунду, то с течением времени мы все равно получим такую же интерференционную картину. Это значит, что каждая частица как бы «раздваивается», проходит через разные пути, а затем собирается в одной точке.

Ведущий: Почему тогда это называют мысленным экспериментом? Можно ли его реально провести?

Гость: В принципе, да, но в такой форме это не делается на практике. Однако волновые свойства электронов действительно наблюдались еще в 1926 году в дифракции на кристалле. Кристалл — это чередующиеся плоскости атомов, и, проходя через него, электроны создают интерференционную картину.

Роль наблюдения и измерения

Ведущий: Какую роль играет наблюдатель в этом эксперименте? Я слышал, что, когда мы начинаем наблюдать за частицей, она перестает вести себя как волна. Это правда? Или я неправильно понял? Объясни, пожалуйста.

Гость: Да, ты прав, но здесь лучше говорить не о наблюдении, а об измерении. Для того чтобы частица начала вести себя как волна или как частица, не требуется осознанный наблюдатель. Дело в том, что если в ходе эксперимента мы можем узнать, через какую щель прошел электрон, интерференционная картина на экране исчезнет. Например, можно между щелями поставить лампочку, чтобы улавливать световые фотоны, которые отражаются от электрона. Так мы узнаем, через какую щель он прошел, и это разрушит картину интерференции. Вместо нее на экране появятся два пятна, как мы и ожидали бы на основе повседневного опыта.

$$\tikzset{every picture/.style={line width=0.8pt}} \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1,font=\sffamily] \draw (130,80) -- (130,144) ; \draw (130,154) -- (130,176) ; \draw (130,186) -- (130,250) ; \draw[blue,domain=-85:85, smooth, variable=\y, samples=100] plot ({200+4000*(sin(-(\y-25)*7)/(\y-25))^2+4000*(sin(-(\y+25)*7)/(\y+25))^2}, 165+\y); \draw (190,80) -- (190,250) ; \draw (145,165) ellipse (8 and 8) ++(6, 6) -- ++(-12, -12) ++(12, 0) -- ++(-12, 12); %Shape: Inductor [id:dp3454355331692156] \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165.5) -- (130,181) -- (190,190) ; \draw [dash pattern={on 0.84pt off 2.51pt}] (45,164.5) -- (130,149) -- (190,140) ; \draw (130,197) node [anchor=west][inner sep=2pt] {Лампа}; \draw (40,175) node [anchor=north][inner sep=5pt] {\shortstack[l]{Источник\\\rule[-0.1mm]{0pt}{2.5mm}электронов}}; \draw (295,205) node [blue] {\shortstack{Интенсивность}}; \end{tikzpicture} $$

Ведущий: Подожди, это сложный момент. Получается, что если мы просто пытаемся измерить, через какую щель прошел электрон, то на экране исчезает интерференционная картина. Вместо нее остается только суммарное изображение частиц, прошедших через каждую щель по отдельности, как это и должно быть для обычных частиц. Выглядит почти как магия, ведь мы ничего не делаем, а просто пытаемся измерить. Это что, частица как-то «чувствует», что ее измеряют? Может она — живой организм, который понимает, осознает, что его кто-то измеряет?

Гость: Нет, конечно, частица — не живой организм и не осознает, что ее измеряют. В квантовой механике сам процесс измерения влияет на систему. В отличие от классической физики, здесь невозможно сделать это воздействие сколь угодно малым. Как только мы что-то измеряем, мы вносим изменения в систему. Например, чтобы определить положение электрона, нужен свет высокой частоты, фотоны которого обладают высокой энергией. Эти фотоны, отклоняясь в результате столкновения с электронами, передают им часть импульса и изменяют их состояние. В результате вся интерференционная картина разрушается.

Ведущий: То есть магии всё-таки в этом никакой нет?

Гость: Никакой. Это объясняется соотношением неопределенностей Гейзенберга. Оно гласит, что невозможно одновременно точно измерить и положение, и импульс частицы, то есть узнать, где именно находится частица и куда движется.

Ведущий: То есть, получается, наблюдение — это когда мы пытаемся заставить что-то взаимодействовать с чем-то еще, например, с прибором?

Гость: Да, именно с прибором.

Ведущий: А прибор фиксирует нечто, что похоже на энергию, верно?

Гость: Не обязательно только энергию, а любую физическую величину. Энергия — возможный пример.

Ведущий: То есть измерить энергию в таких маленьких масштабах мы можем только через воздействие другой энергией, направленной на объект наблюдения. Правильно?

Гость: Да, для элементарных частиц это действительно так.

Ведущий: Значит, мы направляем энергию на объект наблюдения, и тем самым изменяем его состояние, вносим возмущение в систему. Верно?

Гость: Совершенно верно.

Ведущий: Это многое мне проясняет! Получается, что элементарные частицы ведут себя, в каком-то смысле, похоже на шарик. Мы наблюдаем шарик тоже благодаря свету, который на него падает. Представим, что где-то в пространстве есть мячик, достаточно большой, чтобы его удержать в руке. Мы видим его, потому что он взаимодействует с частицами света.

Гость: Да, это так.

Ведущий: Если уменьшить этот шарик до размера атома или электрона и освещать его высокочастотным светом, то свет начинает сбивать его с места, внося возмущения. Правильно?

Гость: Да, именно так. Но нужно уточнить, что электрон, по современным представлениям, не имеет размера, поэтому лучше говорить о размере атома или атомного ядра.

Ведущий: Нет размера потому, что электрон как бы «размыт» в пространстве, когда мы его измеряем?

Гость: Нет, «размываются» в пространстве любые микрообъекты, например, атомы. В отличие от них электрон взаимодействует в одной точке. Например, фотопластинка чернеет только в одном месте, и это действительно точка. Мы не можем измерить размер этой области взаимодействия — он меньше $$10^{-16}$$ или даже $$10^{-17}$$ сантиметров.

Вероятностная природа квантовой механики, коллапс волновой функции и классический предел

Ведущий: Мы коснулись момента измерения, но для меня всё еще не до конца понятно вот что: почему, как только мы начинаем воздействовать на электрон в момент прохождения через щель, мы вмешиваемся в его поведение? Почему он перестает быть волной и становится частицей?

Гость: Это действительно загадочное поведение, которое постулируется в аксиомах квантовой механики и носит название «коллапс волновой функции». По аксиоме коллапс происходит в момент измерения, когда квантовая система взаимодействует с классическим объектом, например, с прибором. Это один из интересных аспектов квантовой механики. В отличие от классической механики, которая замкнута и не требует дополнительных предположений, квантовая механика нуждается в понятии классического прибора для своей формулировки. В пределе крупных тел квантовая механика действительно переходит в классическую, но сама квантовая теория в основе остается «логически незавершенной».

Ведущий: Получается, квантовая и классическая механика — это не полностью изолированные друг от друга теории?

Гость: Да, строго говоря, квантовая механика не является логически замкнутой. Кто-то может даже сказать, что она не полностью логически корректна. Но тем не менее это не мешает ей работать. Все ее предсказания подтверждаются экспериментально и в ее правильности ученые не сомневаются.

Ведущий: То есть, если в 10 из 10 случаев мы измеряем электрон во время прохождения через щель, мы видим его как точку на экране?

Гость: Совершенно верно. Но тут важно отметить, что мы не можем предсказать, куда конкретно попадет каждый отдельный электрон. В принципе он может казаться в произвольном месте. Лишь совокупная картина прохождения огромного числа электронов дает стабильный интерференционный узор. Квантовая механика позволяет предсказывать только вероятность исхода эксперимента, а не конкретный результат для каждого случая. Это принципиальное отличие квантовой механики от классической физики.

Ведущий: Означает ли это, что один электрон сам по себе непредсказуем, а масса электронов становится предсказуемой? И в какой момент квантовая механика превращается в классическую? Правильно ли считать, что квантовая механика описывает только один электрон, а массу электронов уже нет?

Гость: Квантовая механика остается применимой даже для больших масс электронов, так как интерференционная картина — это результат наложения всех электронов на фотопластинку. Переход к классической физике происходит при увеличении массы и размеров системы. Соотношение неопределенностей Гейзенберга является критерием квантовости или классичности: оно утверждает, что произведение неопределенностей координаты и импульса не может быть меньше постоянной Планка:

$$\Delta x\Delta v\geq{h\over m}.$$

Для макроскопических тел, таких как мячик, произведение погрешностей в определении координат и импульса и так гораздо больше постоянной Планка, и поэтому они ведут себя классически. Но если произведение предполагаемых погрешностей для объекта достигают значений меньше постоянной Планка, то вступает в действие квантовая механика — и неопределенность в положении или импульсе возрастает из-за квантовой природы объекта.

Например, тот же электрон в кинескопе движется по вполне классическим траекториям. Возможное «расплывание» из-за квантовой природы оказывается пренебрежимо мало по сравнению с размерами элементов в кинескопе, направляющих электроны в разные части экрана. Совершенно другое дело — электрон в атоме. Из-за малых размеров атома электрон «расплывается» в облака, о которых рассказывают на уроках химии.

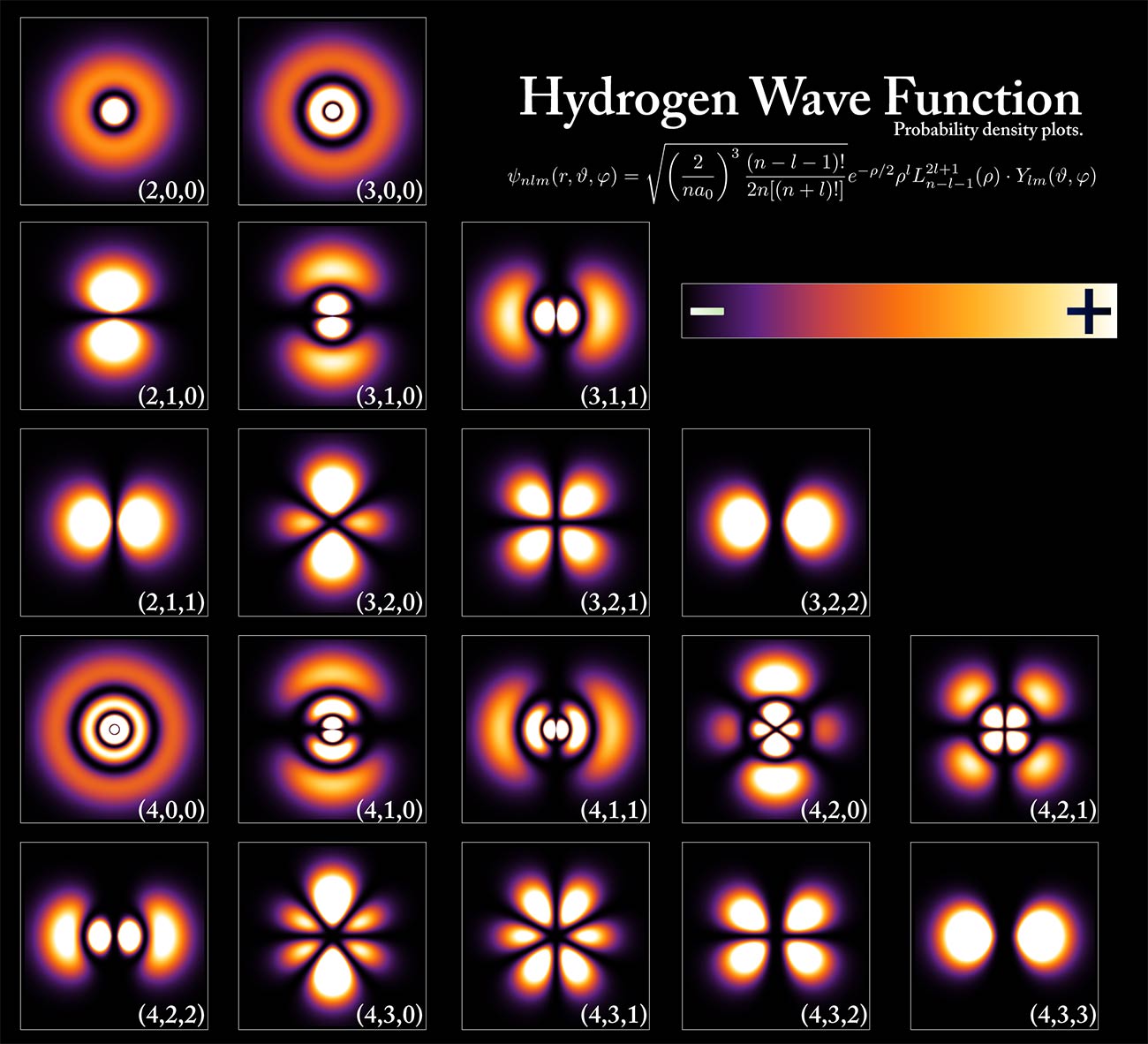
Никаких траекторий у электрона в атоме нет. И именно из-за этого размытия, из-за квантовой природы электронов они не «падают» на ядра атомов.

Проявление квантовой механики в макромире

Ведущий: Давай попробуем немного пофантазировать. Вот этот квантовый мир, о котором мы говорили — является ли он движущей силой всего, что мы видим вокруг? Или то, что происходит на квантовом уровне, никак не влияет на нас как наблюдателей? Расскажи, пожалуйста, об этом, потому что это сложно представить и понять.

Гость: Это действительно сложный вопрос. Насколько квантовая природа микромира влияет на наш макромир? Можно сказать, что само существование атомов и тел, построенных из атомов, связано с квантовой механикой. Как я уже говорил, только квантовая механика может объяснить, почему электрон «вращается» вокруг ядра и не падает на него. В курсе квантовой механики студенты решают такую задачу о поведении электрона в поле притяжения ядра. У такой системы есть дискретный набор уровней, на которых может находиться электрон. Есть уровень с наименьшей энергией, и ниже этой энергии электрон не опустится. Поэтому атомы и существуют.

Ведущий: Насколько я понимаю, главная проблема современной физики — это невозможность объединить ньютоновскую механику и квантовую. Действительно ли это важная задача?

Гость: Я бы не назвал это проблемой, потому что ньютоновская механика — следствие квантовой. Можно сделать предельный переход и получить второй закон Ньютона из квантовой механики. Современная проблема больше связана с объединением гравитации и квантовой механики. Гравитация описывает Вселенную на огромных масштабах, где размеры галактик становятся малы. Теория гравитации, то есть общая теория относительности, является классической и не учитывает квантовые эффекты.

Ведущий: Но ведь она замечательно работает?

Гость: Да, потому что на таких расстояниях и с такой массой квантовые эффекты несущественны. С другой стороны, в микромире гравитация слаба и ее не учитывают. Проблема возникает, когда мы пытаемся построить квантовую теорию гравитации, важную для описания черных дыр и ранних моментов Вселенной после ее рождения.

Ведущий: То есть в конечном итоге физика стремится понять, что же мы такое?

Гость: Да, именно так.

Вглубь материи

Ведущий: Ты упомянул гравитацию и сказал, что на уровне атомов и, тем более, электронов она крайне незначительна. Расскажи об этом подробнее. В интернете есть сайты и программы, где можно посмотреть масштабы Вселенной — от атомов до молекул, бактерий, насекомых, человека, планет. Это действительно впечатляет, ведь ощущаешь свою незначительность. Но если смотреть в другую сторону, к меньшим размерам, можно ли представить себе, что такое атом? Объясни, как физик и как человек: что такое атом?

Гость: Атом — это положительно заряженное ядро, в котором находятся протоны и нейтроны, и вокруг него «вращаются» электроны.

Ведущий: То есть атом — это не просто структура, а результат взаимодействия сил?

Гость: Можно сказать, что это система взаимодействующих частиц.

Ведущий: Понял. А из каких частиц состоят протоны и нейтроны?

Гость: Протоны и нейтроны — это сложные объекты, не точечные, в отличие от электронов.

Ведущий: Но ты же сказал, что это частицы. Тогда почему они не считаются точечными объектами? Разве они не подчиняются законам квантовой механики?

Гость: Конечно, подчиняются. Например, при рассмотрении атома, размер которого около $$10^{-8}$$ сантиметров, можно считать протон точечным, ведь его размер составляет около $$10^{-13}$$ сантиметров. Пяти порядков разницы достаточно, чтобы пренебречь размерами протона и упростить расчеты. Но если рассматривать процессы на меньших расстояниях, то для этого нужно увеличивать энергию взаимодействия.

Ведущий: То есть, чтобы исследовать меньшие масштабы, требуется повышать энергию из-за принципа неопределенности. Чем точнее мы хотим определить координаты, тем больше нужно увеличить неопределенность импульса, а значит, и сам импульс, то есть энергию частиц.

Гость: Абсолютно верно. Например, при столкновении протонов с электронами отклонение последних указывает на то, что протоны не являются точечными объектами. Внутри протона находятся другие точечные объекты — кварки, которые взаимодействуют между собой через глюоны. Таким образом, протон состоит из трех кварков, связанных глюонами.

Ведущий: Это самые маленькие частицы, о которых мы знаем, или есть еще меньше?

Гость: В принципе, да. На данный момент кварки и глюоны считаются точечными частицами, как и электроны.

Ведущий: Насколько я понимаю, у кварков и глюонов есть разные типы, верно?

Гость: Да, есть. В физике элементарных частиц выделяют несколько поколений частиц. Первое поколение включает легкие кварки, которые входят в состав протонов и нейтронов. Сюда также относятся электрон и электронное нейтрино — частица, почти лишенная массы, которая возникает при некоторых распадах. Например, свободный нейтрон распадается на протон, электрон и антинейтрино примерно за 15 минут.

Существует также второе и третье поколение, которые по составу похожи на первое, но различаются массой. Второе поколение тяжелее первого, а третье — тяжелее второго.

Ведущий: Сложно представить, насколько они маленькие. Они тоже точечные частицы?

Гость: Да, кварки и лептоны считаются точечными частицами, то есть не имеют размеров, как мы их понимаем.

Ведущий: Что ты имел в виду под лептонами?

Гость: Лептоны — это частицы, которые не участвуют в сильных взаимодействиях. Современная физика выделяет четыре типа взаимодействий: гравитационное, электромагнитное, слабое и сильное. Лептоны, например, участвуют только в слабых и электромагнитных взаимодействиях.

Ведущий: То есть мы говорим о взаимодействиях на квантовом уровне?

Гость: Да, это взаимодействия на уровне микромира. Протон существует за счет сильных взаимодействий, которые переносятся глюонами. Электроны, относящиеся к лептонам, участвуют только в слабых и электромагнитных взаимодействиях и не подвержены сильным.

$$ \begin{tikzpicture}[font=\sffamily,column 1/.style={black!70!orange,nodes={fill=yellow!70!orange,rounded corners}}, column 2/.style={black!50!orange,nodes={fill=yellow!70!orange,rounded corners}}, column 3/.style={black!50!orange,nodes={fill=yellow!70!orange,rounded corners}}, column 4/.style={black!50!blue,nodes={fill=green!40!yellow,rounded corners}}, column 5/.style={red!50!blue,nodes={fill=red!80!blue!30!white,rounded corners}} ] \matrix[column sep={10pt},row sep=10pt,nodes={minimum size=8mm,inner sep=0}] { \node (u){u}; & \node{c}; & \node {t}; &[6mm] \node (g){$\gamma$}; &[7mm] \node (h){H}; \\ \node {d}; & \node{s}; & \node {d}; & \node (g2)[shift={(0,-1mm)}] {g}; \\[1mm] \node (n1){$\nu_e$}; & \node{$\nu_\mu$}; & \node (n3){$\nu_\tau$}; & \node [shift={(0,1mm)}]{$Z^0$};\\ \node (e){$e$}; & \node{$\mu$}; & \node {$\tau$}; & \node {$W^{\pm}$};\\ }; %\node [inner ysep=7mm,inner xsep=0,anchor=south west] at (u.north west) {\bf\sffamily Фундаментальные частицы стандартной модели} \node [inner ysep=1mm,inner xsep=0,anchor=south west] at (u.north west) {Кварки} \node [inner ysep=1.4mm,inner xsep=0,anchor=south west] at (n1.north west) {Лептоны} \node [inner ysep=1.8mm,inner xsep=0,anchor=south west] at (g.north west) {Бозоны} \node [inner ysep=0.8mm,inner xsep=0,anchor=north west] at (e.south west) {\footnotesize электрон} \node [inner ysep=0.0mm,inner xsep=0,anchor=north west] at (n1.south west) {\footnotesize нейтрино} \node [inner sep=0,anchor=north west] at (g.south west) {\footnotesize фотон} \node [inner ysep=0.8mm,inner xsep=0,anchor=north west] at (g2.south west) {\footnotesize глюон} \node [inner ysep=1.8mm,inner xsep=0,anchor=south west] at (h.north west) {Бозон Хиггса} \end{tikzpicture} $$

Бозон Хиггса

Ведущий: Недавнее открытие бозона Хиггса стало очень известным. Что оно нам дает для понимания квантовой механики? Я так понимаю, это важно как для классической, так и для квантовой механики.

Гость: Квантовая механика описывает поведение самых разных систем, в том числе даже вымышленных. Она не определяет, какая из них реализована в нашем мире. В физике элементарных частиц есть «стандартная модель», которая и говорит, какие частицы существуют и как они взаимодействуют. Чтобы сформулировать стандартную модель, в нее нужно было добавить частицы, еще не открытые на опыте. Примерно так же, как Менделеев оставил места в своей таблице для еще не открытых элементов, когда открыл периодический закон.

В стандартной модели были предсказаны несколько частиц до их открытия, и позже они были найдены экспериментально. Например, векторные бозоны $$W^{\pm}$$ и $$Z^0$$, с-кварк из второго поколения, t-кварк из третьего поколения. Бозон Хиггса был последней предсказанной частицей, и вот его наконец-то открыли.

Ведущий: Это открытие что-то меняет в нашем понимании Вселенной?

Гость: По большому счету, не так уж и много, ведь большинство физиков были уверены, что этот бозон существует. Стандартная модель хорошо описывала результаты всех экспериментов в физике частиц с 60-х годов, и открытие бозона Хиггса стало ее очередным триумфом.

Ведущий: Значит, открытие последнего бозона — просто подтверждение теории?

Гость: Да, фактически так.

Ведущий: Но зачем тогда нужен был Большой адронный коллайдер? Почему было затрачено столько денег и усилий только на подтверждение теории, которая уже работает?

Гость: Потому что задача поиска бозона Хиггса — это не единственная задача Большого адронного коллайдера (LHC). Ожидания в научном сообществе больше связаны с так называемой новой физикой — процессами, которые выходят за рамки Стандартной модели.

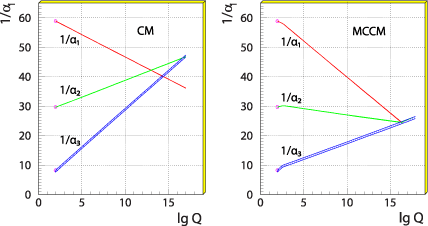
Проще говоря, ученые надеются обнаружить отклонения от стандартной модели. Пока такие отклонения не были найдены, хотя при открытии бозона Хиггса в некоторых каналах его распада, например, на два фотона, зафиксировали небольшое превышение измеренной интенсивности над предсказанной Стандартной моделью. Неопределенность этого результата была велика, и всё оставалось в пределах погрешности. Но некоторые ученые увидели в этом возможные проявления новой физики и пытались объяснить их в своих моделях.

Через некоторое время по мере получения всё новых и новых данных выяснилось, что в одном из экспериментов, проводимых на установке ATLAS, интенсивность начала снижаться и стала ближе к значениям Стандартной модели. В другом крупном эксперименте — CMS — новые данные также показали, что превышения уже нет.

Ведущий: То есть никакой новой физики пока не предвидится?

Гость: Похоже, что пока действительно нет, и найденный бозон, скорее всего, просто хиггсовский бозон стандартной модели.

Ведущий: Понятно, было очень интересно!