Сложение вращений и анимация в TikZ
В рекомендациях ютуба мне часто попадалась задачка о вращающихся окружностях. Вот её формулировка: окружность катится без проскальзывания по другой окружности втрое большего радиуса и совершает вокруг неё один оборот. Сколько оборотов при этом она совершит вокруг своего центра?
Эта задача встречалась в американском тесте абитуриентов 1982 года и примечательна тем, что среди предложенных вариантов ответов не было правильного. Сама задача, её история и связанные вопросы разобраны в этом видео:
Я вспомнил об этой задаче, потому что, наконец, разобрался как делать анимации в TikZ, и теперь вместо множества слов могу просто показать анимированные иллюстрации.
В этой задаче кажущийся ответ — три оборота — неправильный. Оборотов будет на 1 больше, чем отношение радиусов. В этом можно убедиться напрямую, просто подсчитав количество оборотов. Я сомневаюсь, что
$$\dvisvgm\definecolor{cyan}{RGB}{0, 200, 250} \shorthandoff{"} \usetikzlibrary {shapes.geometric} \usetikzlibrary{animations} \begin{tikzpicture} \def\a{1} \def\b{3} \useasboundingbox (-\b-2*\a-0.1,-\b-2*\a-0.1) rectangle (\b+2*\a+0.1,\b+2*\a+0.1); \draw[cyan,very thin] (-\b-2*\a,-\b-2*\a) grid (\b+2*\a,\b+2*\a); \node[star,star points=57, star point ratio=1.07,minimum size=6.2cm, draw,fill=white] at (0,0); \draw[purple,fill] (0:\b) circle (1pt) -- (0,0) circle (1pt) node [midway, sloped, above] {$\b$} ; \begin{scope}:rotate = {0s="0", (5*\b)s="360",repeats} \begin{scope} :rotate = {0s="0", (5*\a)s="360", origin={(\b+\a,0)}, repeats} \node [star,star points=19, star point ratio=1.2,minimum size=2.2cm, draw,fill=white] at (0:\b+\a) {}; \draw [purple,fill] (0:\b+\a) circle (1pt) -- (0:\b) circle (1pt) node [midway, sloped, above] {$\a$} ; \end{scope} \end{scope} \coordinate (A) at (1,1.5); \node [fill=white,inner sep=1pt,anchor=east,xshift=3pt,yshift=-1pt] at (A) {$\text{обороты: }\,\,\,.$}; \foreach \t in {3,2,...,0} { \node :opacity = { 3.75*(0) s="0", 3.75*(0+\t) s="0", 3.75*(0.001+\t) s="1", 3.75*(0.999+\t) s="1", 3.75*(1+\t)s="0", 3.75*(4) s="0", repeats } [anchor=east,inner sep=1pt] at (A) {$\t$}; } \foreach \t in {0,1,...,9} { \node :opacity = { 0.375*(0) s="0", 0.375*(0+\t) s="0", 0.375*(0.01+\t) s="1", 0.375*(0.99+\t) s="1", 0.375*(1+\t)s="0", 0.375*(10) s="0", repeats } [anchor=west,inner sep=1.5pt] at (A) {$\t$}; } \end{tikzpicture}$$
Конечно, задачу можно решить стандартным геометрическим подходом: рассмотреть углы между радиусами к точкам касания в начальном и текущем положениях, и приравнять длины дуг между этими точками. Но как быть, если задачу надо решить в уме? Ход рассуждений может быть следующим.
Представим оборот меньшей окружности вокруг большей как сумму двух движений. В первом движении окружности вращаются так, что их центры остаются неподвижными. В этом случае малая окружность действительно совершит три оборота, пока большая окружность совершает один оборот. Второе движение — это вращение обеих окружностей, соприкасающихся в одной точке, на ещё один оборот. При сложении двух движений обороты большой окружности оказываются разнонаправленными и компенсируются, а обороты малой окружности — однонаправленными и суммируются, то есть малая окружность совершит четыре оборота. На следующей иллюстрации этой идеи легко подсчитать количество оборотов каждой окружности в полном цикле:
$$\dvisvgm\definecolor{cyan}{RGB}{0, 200, 250} \usetikzlibrary {shapes.geometric} \usetikzlibrary{animations} \begin{tikzpicture} \def\a{1} \def\b{3} \useasboundingbox (-\b-2*\a-0.1,-\b-2*\a-0.1) rectangle (\b+2*\a+0.1,\b+2*\a+0.1); \draw[cyan,very thin] (-\b-2*\a,-\b-2*\a) grid (\b+2*\a,\b+2*\a); \begin{scope}:rotate = {0s="0", 5s="-360", 6s="-360", 11s="0", 12s="0", repeats} \node[star,star points=57, star point ratio=1.07,minimum size=6.2cm, draw,fill=white] at (0,0); \draw[purple,fill] (0:\b) circle (1pt) -- (0,0) circle (1pt) node [midway, sloped, above] {$\b$} ; \end{scope} \begin{scope} :rotate = {0s="0", 6s="0", 11s="360", 12s="360", origin={(0,0)}, repeats} \begin{scope} :rotate = {0s="0", 5s="1080", 6s="1080", 11s="1080", 12s="1080", origin={(\b+\a,0)}, repeats} \node [star,star points=19, star point ratio=1.2,minimum size=2.2cm, draw,fill=white] at (0:\b+\a) {}; \draw [purple,fill] (0:\b+\a) circle (1pt) -- (0:\b) circle (1pt) node [midway, sloped, above] {$\a$} ; \end{scope} \end{scope} \end{tikzpicture}$$
Самодельная типографская раскладка
В повседневном использовании мне не хватает двух символов на русской раскладке клавиатуры: решетки # и собаки @. Решетка обозначает заголовки в распространенной разметке markdown, а собака применяется в адресах электронной почты в чатах, чтобы «тегать» определенных людей (@supercoder) или всех подряд (@channel).
Для ввода решетки и собаки приходится постоянно переключаться с русского языка на английский и назад, да и сами эти символы вводить с шифтом. Ещё у Windows случается баг, когда она переключает язык не сразу, а после небольшой паузы: ты нажал Alt + Shift и уже
Природу неудобства с этими специальными символами легко понять. Применять их в маркдауне и в чатах придумали в англоязычной среде с расчетом на англоязычную среду, когда никакой язык переключать не нужно. В других языках приходится терпеть.
Много лет назад я устанавливал типографскую раскладку Ильи Бирмана. Она специальным образом задействует правую клавишу Alt для ввода с клавиатуры расширенного набора символов. Например, вместо копирования
Казалось бы, сам бог велел сделать в типографской раскладке не зависящие от языка комбинации клавиш Alt + 2 и Alt + 3 для ввода собаки и решетки. Тем более, так уже сделано и для знака доллара $ с комбинацией Alt + 4, и для квадратных скобок, которые тоже нужны в маркдауне. Но у Ильи в раскладке через Alt + 2 и Alt + 3 вводятся символы верхних индексов ² и ³. Сегодня такое решение кажется устаревшим. Я, кстати, вообще не помню, чтобы хоть раз в жизни использовал верхние индексы именно как эти отдельные символы, а не через инструменты форматирования.
Илья делал свою раскладку в программе MSKLC (Microsoft Keyboard Layout Creator). И нам никто не мешает создать собственную раскладку, отталкиваясь от своих потребностей. К счастью, MSKLC позволяет импортировать любую установленную раскладку и затем её отредактировать.
Я оставил большинство дополнительных символов как у Ильи. Единственные изменения — это прямой ввод символов `@# через комбинацию с правым Alt.
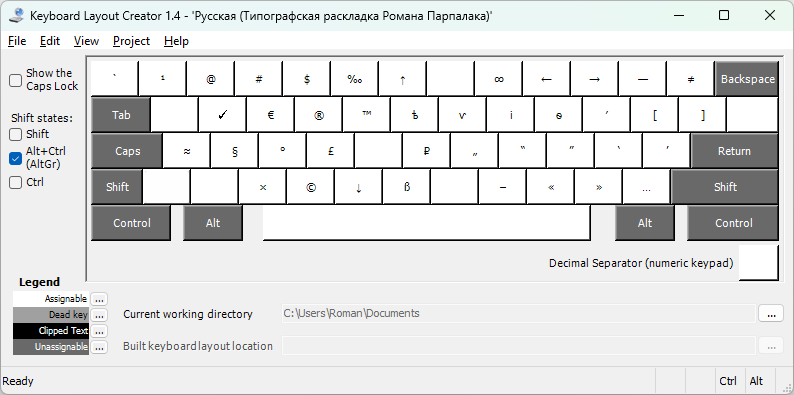
Стоит отметить, что программа MSKLC давно не обновлялась. Это заметно и по ее внешнему виду, и по требованию скачать древнюю версию .NET Framework 3.5 SP1 2008 года. К счастью, эти трудности не помешали создать свою версию раскладки.
Ещё одно интересное наблюдение заключается в том, что раньше типографская раскладка у меня не прижилась, потому что она ломает сочетание клавиш правый Alt + Enter для перехода в полноэкранный режим. Дискомфорт от сломанной привычки оказался сильнее пользы, которую приносила раскладка. Сейчас же я не испытываю особого дискомфорта. Похоже, изменения в интерфейсах и способах просмотра видео привели к тому, что жест правый Alt + Enter потерял своё значение.
Подключил Akismet для борьбы со спамом
Со временем технологии развивались, и через selenium разработчики автоматизировали действия ботов через полноценные браузеры. Метод защиты с помощью Javascript стал фильтровать только самых тупых ботов.
Затем для борьбы со спамом я включил предарительную проверку комментариев перед публикацией. К этому времени поток комментариев на сайте как раз уменьшился. Немногочисленные нормальные комментарии легко одобрить вручную, особенно когда отвечаешь на них. Тогда же я запрограммировал обход предварительной проверки для залогиненных модераторов — пользователей, которые управляют отображением комментариев.
Чтобы облегчить себе жизнь по окончательному удалению спаммерских комментариев из очереди на модерацию, я задумался над тем, какова цель спаммеров? Конечная цель — разместить ссылки для манипуляции индексом цитирования и для привлечения посетителей. Если запретить оставлять ссылки, спаммерам не будет смысла оставлять комментарии без них. А если ссылку хочет разместить человек в хорошем комментарии, сайт скажет ему, чтобы он удалил http:// из ссылки. Запрет на ссылки принес свои плоды, но
Сейчас я решил посмотреть, как привлечь новые технологии для фильтрации спама. Теоретически можно натренировать нейросеть на
Akismet — это система фильтрации спама в комментариях, разработанная авторами WordPress. В вордпрессе есть плагин, который обращается к API Akismet. Однако сам API открыт и может быть использован любым сайтом, для обращения нужен только лицензионный ключ. Лизензия для некоммерческого использования бесплатная.
Основная особенность Akismet заключается в том, что он используется на множестве сайтов. Таким образом можно быстро выявлять новые
Я подключил сервис и несколько дней его тестировал. По каждому комментарию Akismet возвращает свое решение: либо это хороший комментарий, либо спам, либо «вопиющий» (blatant) спам. В итоге остановился на следующем алгоритме фильтрации комментариев:
- если комментарий хороший, он публикуется сразу;
- если комментарий признан вопиющим спамом, он даже не сохраняется, при попытке его отправить будет возвращено сообщение об ошибке;
- если комментарий спаммерский, он остается скрытым, а уведомление о нем отправляется модераторам;
- если владелец сайта не указал в настройке лицензионный ключ Akismet или если сервис не ответил, комментарий либо публикуется либо остается скрытым в зависимости от того, включен ли режим модерации (откат к старому алгоритму).
После внедрения за две недели пришло 62 комментария. Из них 60 спаммерских комментариев были отсеяны либо как вопиющий спам (21 комментарий), либо как спам с наличием ссылок в тексте. Остальные два комментария опубликованы: один хороший комментарий и один спаммерский со ссылкой на yotube.

Понятно, что у способа есть свои недостатки.
Задача о шпионах за круглым столом
Попалась тут задача, в которой ChatGPT меня обошел. Я хотел придумать

Условие
На банкете за круглым столом сидят $$n$$ шпионов. Каждый шпион независимо от остальных случайным образом выбирает одного из двух соседей — левого или правого — и подсыпает яд ему в бокал. Каково математическое ожидание числа выживших шпионов?
$$\usetikzlibrary{arrows.meta} \begin{tikzpicture}[scale=1.4] \tikzset{spy/.style={circle,draw,minimum size=6mm,inner sep=1pt}} \foreach \i [evaluate=\i as \angle using 360/8*(\i-1)] in {1,...,8} { \node[circle, minimum size=6mm, inner sep=1pt] (spy\i) at (\angle:1.5); \coordinate (below\i) at (\angle:1.1); } \foreach \a/\b in {1/2, 2/1, 3/4, 4/5, 5/4, 6/7, 7/6, 8/1} { \draw[-{Stealth[length=1.6mm]}] (spy\a) to[bend right=15] (spy\b); } \foreach \i in {3,8} { \node[spy,green!40!black,fill=green!10!white] at (spy\i) {\i}; \node[green!60!black] at (below\i) {$\checkmark$}; } \foreach \i in {1,2,4,5,7,6} { \node[spy, red!50!black,fill=red!10!white] at (spy\i) {\i}; \node[red!80!black] at (below\i) {$\dagger$}; } \end{tikzpicture} $$
Говоря простыми словами, нам надо найти среднюю долю выживших при многократном повторении эксперимента.
Решение
Пусть шпионы пронумерованы по кругу числами от 1 до $$n$$ (шпион $$n$$ считается соседом шпиона 1). Обозначим через $$X$$ количество выживших шпионов. Требуется найти математическое ожидание $$\mathbb{E}[X]$$.
Рассмотрим судьбу одного конкретного шпиона, скажем, с номером $$i$$. Он погибает в том и только в том случае, если хотя бы один из соседей выбрал его целью. Таким образом, шпион $$i$$ выживает, если и шпион $$i-1$$, и шпион $$i+1$$ выбрали не его. Поскольку выбор жертв происходит независимо, и каждый выбирает левого или правого соседа с вероятностью 1/2, вероятность того, что оба соседа шпиона $$i$$ выбрали другого соседа, равна:
$$ \mathbb{P}(\text{шпион }i\text{ выживает})=\left(\frac{1}{2}\right)^2=\frac{1}{4}. $$
Введем индикаторную случайную величину $$X_i$$, равную 1, если шпион $$i$$ выживает, и 0 в противном случае. Тогда общее число выживших:
$$X=\sum_{i=1}^n X_i.$$
Так как все шпионы находятся в равных условиях, математическое ожидание $$\mathbb{E}[X_i]$$ одинаково для всех и вычисляется по определению:
$$\mathbb{E}[X_i]=0\cdot\mathbb{P}(\text{шпион }i\text{ умирает})+1\cdot\mathbb{P}(\text{шпион } i \text{ выживает})={1\over4}.$$
Следовательно, по линейности математического ожидания:
$$\mathbb{E}[X]=\sum_{i=1}^n\mathbb{E}[X_i]=n\cdot\frac{1}{4}=\frac{n}{4}.$$
Таким образом, в среднем выживает четверть шпионов, независимо от их числа.
Обсуждение решения и ошибок
ChatGPT получил правильную формулу только для $$n>2$$. Если $$n=2$$, то ответ $$n/4=1/2$$ неправильный, так как в этом случае сосед слева и справа — один и тот же человек, и оба шпиона отравят друг друга. И для $$n=1$$ ответ тоже неприменим.
Самый неочевидный шаг в этом решении — переход от $$\mathbb{E}[X]$$ к $$\mathbb{E}[X_1]+\mathbb{E}[X_2]+\ldots+\mathbb{E}[X_n]$$. Если бы случайные величины $$X_i$$ были независимы, например, как результаты многократного подбрасывания монеты, никого бы не удивило математическое ожидание количества орлов, равное $$n/2$$. Но в нашем случае $$X_i$$ зависимы друг от друга. Так, если шпион $$i$$ выжил, то его соседи $$i\pm1$$ точно выбрали своими жертвами шпионов $$i\pm2$$, сидящих через одного от $$i$$, и они гарантированно не выжили. Не повлияют ли такие взаимосвязи на среднее количество выживших?
Оказывается, математические ожидания случайных величин можно складывать, чтобы получить математическое ожидание их суммы, даже если случайные величины зависимы. Я попробую в оставшейся части заметки описать идею доказательства этого утверждения в дискретном случае.
Пространство элементарных событий и математическое ожидание суммы случайных величин
В задачах теории вероятностей рассматривают так называемое пространство элементарных событий $$\Omega$$ — множество всех возможных непересекающихся исходов $$\omega_k$$. Например, в качестве элементарных событий в нашей задаче удобно взять совокупность принятых решений каждым шпионом. Чтобы закодировать элементарное событие, будем выписывать по порядку цифры 0 или 1: 0, если очередной шпион выбрал жертвой соседа слева, и 1 — если справа. Таким образом, каждая последовательность из $$n$$ нулей и единиц соответствует некоторому исходу, то есть некоторому элементарному событию, и наоборот, для каждого исхода можно указать соответствующую последовательность нулей и единиц.
В простых случаях можно перечислить все элементарные события и их вероятности. Например, вот все возможные исходы в нашей задаче:
$$\begin{align*} \omega_0&=000\ldots000,\\ \omega_1&=000\ldots001,\\ \omega_2&=000\ldots010,\\ \omega_3&=000\ldots011,\\ &\ldots\\ \omega_{2^n-2}&=111\ldots110,\\ \omega_{2^n-1}&=111\ldots111.\\ \end{align*}$$
Все они равновероятны, поэтому вероятность каждого исхода $$P(\omega_k)=1/{2^n}$$.
Нам осталось выяснить, какой смысл имеет понятие случайной величины $$X$$ с точки зрения элементарных событий. Для каждого элементарного события случайная величина $$X$$ имеет вполне определенное значение, то есть это обычная функция от $$\omega_k$$. Рассмотрим для примера случайную величину $$X_2$$ из нашей задачи, которая равна 1, если второй шпион выжил, и 0 в противном случае.
$$ \begin{tikzpicture}[scale=1.4] \tikzset{spy/.style={circle,draw,minimum size=6mm,inner sep=1pt}} \foreach \i [evaluate=\i as \angle using 360/8*(\i-1)] in {1,...,8} { \node[circle, minimum size=6mm, inner sep=1pt] (spy\i) at (\angle:1.5); \coordinate (below\i) at (\angle:1.1); } \foreach \a/\b in {3/4, 2/3, 1/8, 4/3, 8/1} { \draw[->] (spy\a) to[bend right=15] (spy\b); } \foreach \i in {2} { \node[spy,green!40!black,fill=green!10!white] at (spy\i) {\i}; \node[] at (below\i) {$a$}; } \node[] at (below1) {$0$}; \node[] at (below3) {$1$}; \node[] at (below4) {$b$}; \foreach \i in {1,3,4,8} { \node[spy, red!50!black,fill=red!10!white] at (spy\i) {\i}; } \node at(2.4,1.05) {$X_2(1a0b...)=1$}; \end{tikzpicture} $$
Так как на второго шпиона влияют только первый и третий шпионы, то значение $$X_2$$ определяется цифрами на первом и третьем месте, а именно $$X_2(0a1b...)=1$$, $$X_2(0a0b...)=X_2(1a0b...)=X_2(1a1b...)=0$$.
Определение математического ожидания случайной величины состоит в том, что это обычное усредение её значения на элементарных событиях с весом, равным вероятности события. Воспользуемся этими знаниями для вычисления математического ожидания суммы элементарных событий:
$$\begin{align*} \mathbb{E}[X]&=\sum_{k=0}^{2^n}X(\omega_k)P(\omega_k)=\sum_{k=0}^{2^n}\left[X_1(\omega_k)+X_2(\omega_k)+\ldots+X_n(\omega_k)\right]P(\omega_k)=\\ &=\sum_{k=0}^{2^n}X_1(\omega_k)P(\omega_k)+\sum_{k=0}^{2^n}X_2(\omega_k)P(\omega_k)+\ldots+\sum_{k=0}^{2^n}X_n(\omega_k)P(\omega_k)=\\ &=\mathbb{E}[X_1]+\mathbb{E}[X_2]+\ldots+\mathbb{E}[X_n]. \end{align*}$$
Как видим, не вполне очевидный шаг замены математического ожидания суммы на сумму математических ожиданий сводится к простому и понятному раскрытию скобок.
Дополнение
Выпишем ответ в явном виде для торопящихся читателей:
$$\mathbb{E}[X]=\begin{cases} 1&\text{при }n=1,\\ 0&\text{при }n=2,\\ \frac{n}{4}&\text{при }n>2. \end{cases} $$
А ещё Евгений Степанищев подтвердил теоретический ответ с помощью моделирования методом
CPU steal time на виртуальном сервере, мониторинг и перцентили
Оказывается, на виртуальных серверах есть специальная метрика CPU steal time. Она показывает, сколько процессорного времени было «украдено» у вашего сервера другими виртуальными машинами на том же физическом сервере. Есть смысл проверить эту метрику, если вы сталкиваетесь с необъяснимыми подтормаживаниями. Их причина может быть не в вашей системе, а в соседях по серверу.
Я периодически сталкиваюсь с этой проблемой на моем хостинге. Она проявляется в том, что изредка база данных обрабатывает запросы в десятки раз медленнее, чем обычно. Отследить такую ситуацию без специальных инструментов почти невозможно, потому что просто ходя по сайту, вы либо не заметите, что на двадцатый раз страница открывалась дольше, либо не поймете причину. Я использую New relic, о чем уже писал.
Изучая статистику после долгого перерыва, опять заметил, что проблема вернулась. Рассмотрел график из
Казалось бы, величина не сильно большая: steal time не превосходит полпроцента, в то время как собственное потребление виртуалки около 5%. Но надо помнить, что это средние значения. Мгновенные значения в отдельные моменты времени могут оказаться гораздо больше. Чтобы их оценить, нужно смотреть на графики перцентилей.
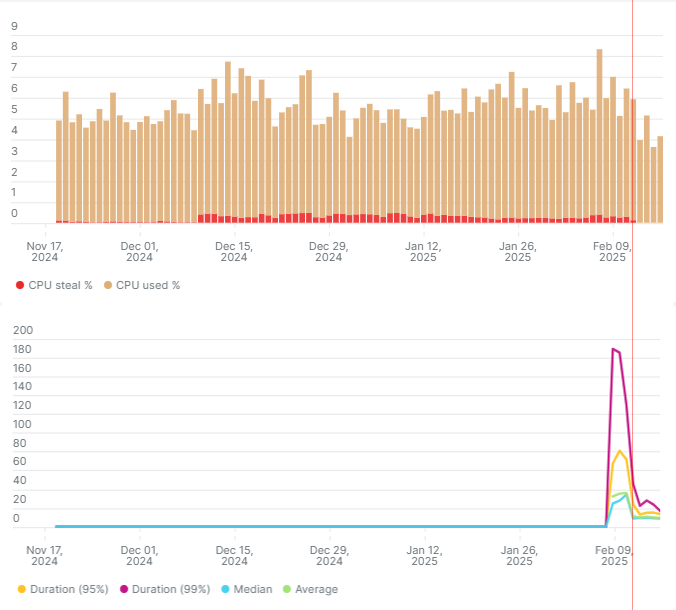
На втором графике я вывел
Что же делать с этой проблемой? Хостеру я писать не стал, скорее всего это бесполезно. Тариф предусматривает общий ресурс процессора, так что наверняка это штатное использование. В таких случаях я делаю временный «ресайз» виртуалки: перехожу на следующий тарифный план с дополнительным количеством памяти и дискового пространства, а потом возвращаюсь назад. С определенной долей вероятности на текущем гипервизоре не будет доступных ресурсов, и система переместит виртуалку на другой гипервизор. Если повезет, то и оборудование будет новее. При возврате к старому тарифному плану виртуалка скорее всего не будет никуда перемещаться.
Я сделал временный ресайз и виртуалка оказалась на другом гипервизоре. Этот момент я отметил на графике красной лииней. CPU steal time упал практически до нуля, перцентили приблизились к среднему и медиане. Среднее время генерации тоже снизилось с 30 до 10 миллисекунд, потому что на гипервизоре оказался более мощный процессор.
Влияние ресайза я обнаружил случайно в сентябре 2023 года, когда хотел проверить, поможет ли увеличение памяти победить непонятные подтормаживания. Эффект был, но не от увеличения объема оперативки, а от перемещения виртуалки на новый гипервизор. Это подтверждает упавший график steal time:
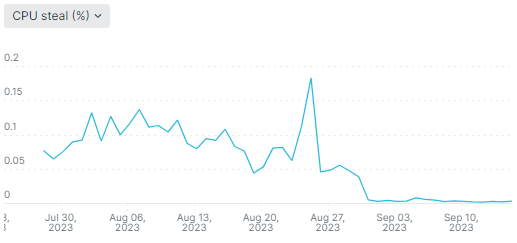
Однако проблема повторилась в декабре 2023 года в большем масштабе, когда steal time подскочил до 8% и дальше стал колебаться около 2%:
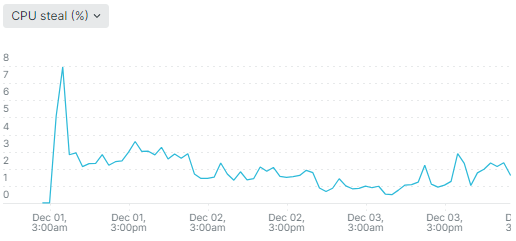
Пришлось опять делать ресайз. Мешающие соседи ушли, однако виртуалка оказалась на гипервизоре с более старым и слабым процессором. Получилось не так удачно, но я не стал дальше испытывать судьбу.
Я стараюсь не злоупотреблять временным ресайзом для переноса виртуалки на более новое железо. Мне кажется, этот прием из серой зоны. С одной стороны, я систему специально не взламываю, пароли не подбираю, уязвимости не ищу и не эксплуатирую, нажимаю только на доступные в интерфейсе кнопки. С другой стороны, цель моих действий — не увеличить ресурсы сервера, а избавиться от мешающих соседей. И хостер, если захочет, может ослеживать и наказывать таких умников.
Нейросети для подготовки текстовой расшифровки речи
Сейчас, в эпоху расцвета нейросетей, опять наткнулся на эту запись и решил на ней потестировать инструменты распознавания речи. В результате получилось
Для распознавания речи
pip install git+https://github.com/openai/whisper.gitРаспознавание запускается простой командой, на входе указывается аудиофайл и язык:
whisper путь_к_файлу.mp3 --language RussianРаботает нейросеть довольно долго, я ждал несколько часов. Это в несколько раз больше длительности самой записи. По мере распознавания команда выводит текст в консоль. Также текст записывается в файл.
Результат в целом оказался качественным, лучше чем можно было ожидать. В расшифровке изредка встречались искаженные слова, но это не сильно затруднило последующую обработку.
Нужно понимать, что точную текстовую расшифровку живого разговора читать очень сложно
Для переработки текста расшифровки я воспользовался ChatGPT.
В итоге последовательность действий получилась такой:
- запустить Whisper и получить сырую расшифровку;
- пройтись по всему тексту и дописать, кто какую реплику говорил;
- копировать главы или фрагменты с обсуждением одной темы в ChatGPT для преобразования разговора в читаемый диалог;
- прочитать и отредактировать текст, переписав и дополнив непонятные места, нарисовать иллюстрации.
На всю работу я потратил столько же времени, сколько занимает подготовка обычной статьи объемом в
Существует ли идеальный код, или новый разработчик всегда хочет всё переписать?
Ситуация в проекте: каждый новый разработчик считает, что имеющаяся кодовая база никуда не годится, в ней сплошной техдолг, от нее надо отказаться и написать всё заново. Кому в этой ситуации доверять? И существует ли объективно идеальный код, или же представление об идеальности кода субъективно, так как всегда найдется критик?
Ответ: настоящий профессионал после изучения кода может прийти к выводу, что весь проект нужно переписать с нуля. Но он не будет останавливать всю разработку на неопределенный срок, переписывать весь код и одномоментно переключаться на него. Он найдет способ писать новый код
Практический совет: доверяйте тому разработчику, который добавляет новые функции в систему за приемлемый срок с меньшим количеством багов. Меньше багов — глубже понимание системы — больше доверия.
Исключение из этого правила возникает тогда, когда разработчик написал систему с нуля тем способом, который не принят в сообществе. Другие разработчики могут не захотеть в нем разбираться не
Философия: действительно, одну и ту же систему можно запрограммировать множеством разных вариантов. Есть ли способ, позволяющий указать, какой из вариантов приближен к идеалу? Я утверждаю, что из всех вариантов кода для каждой программной системы можно выбрать наилучший — наиболее подходящий, в котором функции системы запрограммированы проще всего. Это утверждение я обосновывал, когда рассуждал об абстракциях в физике и программировании.
Технология отбеливания пластика Retrobright
Мне тут достался телефонный аппарат, можно сказать по наследству. Выглядел он ужасно. Весь пожелтевший, как будто всё время находился под прямыми солнечными лучами. Он оказался рабочим и у него хорошо нажимались кнопки, поэтому я решил его восстановить.
Степень пожелтения можно оценить по этой фотографии. На телефонной трубке была наклейка в форме параллелограмма. Я ее снял, и цвет пластика под ней будем считать оригинальным.

Описание технологии отбеливания и примеры результатов читайте на хабре и в блоге Александра Алексеева. Я выбрал способ с гелем для обесцвечивания волос и ультрафиолетовой светодиодной лентой. Гель наносится на поверхность детали и накрывается целлофановой пленкой для предотвращения высыхания. Далее деталь выдерживается в ультрафиолетовом свете.
Я дождался 2 метра светодиодной ленты с Алиэкспресса и купил гель с концентрацией перекиси водорода 12%. Протестировать способ решил на телефонной трубке, обмотав ее светодиодной лентой.

Ближе к концу процесса гель слегка вспенивается от выделяющегося кислорода. Но как показывает практика, на результат это не влияет.

После 7 часов отбеливания я отмыл трубку. Изменения были заметны, но результат с первого раза получился не очень качественным.

Проблема с неравномерностью засветки была самой серьезной. Чтобы ее избежать, я прикрепил ленту змейкой к листу металла и размещал такой импровизированный светильник на небольшом расстоянии от пластика.

Поверхность телефона оказалась слишком большой, поэтому я отбеливал ее в два этапа, засвечивая по частям.

Итоговый результат превзошел все возможные ожидания! Если сильно приглядываться, можно разглядеть, что пластик вокруг клавиатуры чуть более желтый, чем под трубкой, где была тень. Но когда телефон стоит на столе при обычном освещении в комнате, это вообще не заметно.

Белых разводов, как на трубке, на самом телефоне не появилось. Возможно, они сделаны из немного разных материалов. Или трубку могли деформировать, и ее поверхность оказалась покрытой микроповреждениями, пропускающими перекись водорода вглубь. А может причина в перегреве участков трубки от расположенной слишком близко светодиодной ленты.
В целом результатом я доволен, могу рекомендовать к повторению. Я купил 60 миллилитров геля для обесцвечивания волос, для телефона этого хватило с небольшим запасом. Гель наносил старой зубной щеткой на предварительно вымытую поверхность. Ленту запитывал током в 900 миллиампер, при этом напряжение на ней было около 11,5 вольт. Работайте в перчатках и очках, так как концентрированная перекись водорода опасна.
Как отремонтировать убитую дискету
Ютуб порекомендовал ролик о том, что обычные дискеты на 1,44 мегабайта можно отформатировать на больший объем. Я помню один такой способ: взять Дос Навигатор и задать при форматировании объем в 1,6 мегабайт. Дискеты после этого нормально работали на повышенной емкости. В ролике об этом способе, кстати, не рассказали.
Почему я вообще завел речь о дискетах? Оказывается, за все 19 лет существования сайта я не рассказал о том, как их ремонтировал! Пришла пора восстановить этот пробел.
Когда
Тем не менее, я обладал тайным знанием по восстановлению дискет с поврежденной дорожкой номер 0. Часто на отремонтированных дискетах был доступен весь объем в 1,44 мегабайта. Для восстановления нужно всего лишь перевернуть гибкий магнитный диск с одной стороны на другую. Суть фокуса в том, что дорожка номер 0 перестает быть дорожкой номер 0.
Первую дискету, которую я восстанавливал, по незнанию разбирал полностью. Больше всего возни с отодвигаемой шторкой, её сложно не погнуть. Потом наловчился вскрывать дискету только с одной стороны. Этого достаточно, чтобы достать гибкий диск, и не нужно снимать шторку.

Сам диск приклеен к металлическому основанию на клейкое кольцо. В первой дискете я полностью счистил клеевой слой и приклеил обратной стороной на

А вот другой диск со следами ремонта еще держится. Около основания видны прилипшие к остаткам клеевого слоя пылинки и ворсинки:

При должной тренировке починить дискету можно в походных условиях практически без инструментов. Низ дискеты разламывается ножом или линейкой. Металлическое основание диска держим левой рукой, зажимаем его между большим и указательным пальцем. Правой рукой оттягиваем гибкий диск. Его удерживаем через салфетку или другую бумажку, чтобы не повредить поверхность и не оставить отпечатки пальцев. При аккуратных действиях клейкое кольцо остается на металлическом основании. На него приклеивается гибкий диск обратной стороной, для этого его достаточно
Таким способом я отремонтировал в свое время не одну дискету. После ремонта некоторые работали не хуже новых. Понятно, что надежность дискеты после восстановления может быть невысокой, и что файлы надо продублировать на нескольких дискетах. Но так надо поступать и с обычными дискетами, не только с восстановленными.
Применение конечных автоматов в программировании
Когда мы пишем программы, часто управляем состоянием
Для управления состоянием полезно иметь представление о конечных автоматах. Конечный автомат — это математическая модель, состоящая из конечного набора состояний, переходов между этими состояниями и действий, выполняемых при этих переходах. Посмотрим, как можно применить идеи из теории конечных автоматов на примере системы комментариев в блоге.
Проблемы в примере без конечных автоматов
shown. Комментарий создавался сразу опубликованным (shown = 1), и позднее его можно было скрыть (shown = 0).
Зачем вообще скрывать комментарии, если их можно удалить? Я сделал комментарии скрываемыми, чтобы можно было передумать, а также чтобы анализировать комментарии со спамом для борьбы с ним. Например, если с
Потом я решил добавить модерацию — предварительную проверку комментариев перед публикацией. Сделал по аналогии еще один флаг sent, который хранит информацию о том, был ли разослан этот комментарий подписавшимся авторам предыдущих комментариев.
Если режим предварительной проверки выключен, набор состояний остается таким же:
shown=1, sent=1— комментарий опубликован и разослан сразу в момент создания;shown=0, sent=1— комментарий скрыт.
А в режиме с включенной предварительной проверкой появляется новое состояние:
shown=0, sent=0— комментарий в момент создания только записан в БД, его должен одобрить модератор;shown=1, sent=1— комментарий опубликован модератором, в момент публикации он рассылается;shown=0, sent=1— комментарий скрыт после публикации.
За публикацию комментария, находящегося на рассмотрении, отвечала та же кнопка, которая ранее управляла флагом shown. В обработчик ее нажатия добавилось только одно условие: если в момент изменения shown с 0 на 1 комментарий еще не разослан, он рассылался. Таким образом, переходы между этими состояниями можно отобразить в виде такой диаграммы:
$$\usetikzlibrary{arrows} \begin{tikzpicture}[node distance=4cm,font=\sffamily] \tikzset{ mynode/.style={rectangle,rounded corners,draw=black,thick, inner sep=0.7em, text width=7em,text centered}, myarrow/.style={->, >=latex', shorten >=1pt, shorten <=2pt,thick} } \node[mynode,fill=yellow!10] (moder) {\shortstack{На проверке\\\tt shown=0\\\tt sent=0}}; \node[mynode, right of=moder,fill=green!10] (pub) {\shortstack{Опубликован\\\tt shown=1\\\tt sent=1}}; \node[mynode, right of=pub,fill=gray!10] (hidden) {\shortstack{Скрыт\\\tt shown=0\\\tt sent=1}}; \draw[myarrow] (moder) to[in=130,out=50] node[above] {рассылка} (pub); \draw[myarrow] (pub) to[in=130,out=50] (hidden); \draw[myarrow] (hidden) to[in=-50,out=-130] (pub); \end{tikzpicture}$$
Если присмотреться к этой диаграмме, можно заметить недостаток: из состояния «на проверке» можно перейти только в состояние «опубликован», при этом комментарий будет разослан авторам предыдущих комментариев. Но что делать, если комментарий проверку не прошел? Спам хотелось бы отправить напрямую в состояние «скрыт», минуя состояние «опубликован».
Когда я увидел на практике необходимость такого перехода, то запрограммировал новую кнопку «оставить скрытым и не рассылать», которая (внимание!) изменяла значение флага sent с 0 на 1 без фактической рассылки комментариев. Таким образом, поменялся смысл флага sent: раньше он указывал на то, что комментарий был разослан, а теперь указывает на отсутствие необходимости разослать комментарий.
$$\usetikzlibrary{arrows} \begin{tikzpicture}[node distance=4cm,font=\sffamily] \tikzset{ mynode/.style={rectangle,rounded corners,draw=black,thick, inner sep=0.7em, text width=7em,text centered}, myarrow/.style={->, >=latex', shorten >=1pt, shorten <=2pt,thick} } \node[mynode,fill=yellow!10] (moder) {\shortstack{На проверке\\\tt shown=0\\\tt sent=0}}; \node[mynode, right of=moder,fill=green!10] (pub) {\shortstack{Опубликован\\\tt shown=1\\\tt sent=1}}; \node[mynode, right of=pub,fill=gray!10] (hidden) {\shortstack{Скрыт\\\tt shown=0\\\tt sent=1}}; \draw[myarrow] (moder) to[in=140,out=40] node[above] {\shortstack{Одобрить\\ (+рассылка)}} (pub); \draw[myarrow] (moder) to[in=-120,out=-60] node[below] {Оставить скрытым и не рассылать} (hidden); \draw[myarrow] (pub) to[in=140,out=40] node[above] {Скрыть} (hidden); \draw[myarrow] (hidden) to[in=-40,out=-140] node[below,pos=0.7] {Опубликовать} (pub); \end{tikzpicture}$$
В итоге мы получили следующие проблемы:
- состояние комментария определяется косвенно по набору значений отдельных признаков
showиsent; - признак
sentпотерял свой первоначальный смысл, его значение уже не говорит о том, произошла ли рассылка комментария; - признаки, по которым определяется состояние, не могут меняться независимо: например, набор значений
shown=1иsent=0не имеет смысла.
Последний пункт особенно важно осознать: значения shown=1 и sent=0 можно получить либо в результате ошибки в коде, либо прямым редактированием базы данных. Выходит, такая модель данных может кодировать несуществующее состояние, и это свидетельствует об ошибке проектирования.
Если мы продолжим дорабатывать систему таким же путем, проблемы при масштабировании усугубятся. По мере добавления новых состояний системы количество флагов будет расти, что усложнит логику проверки состояния. Сама проверка может происходить в нескольких местах, что потребует копирования этой сложной логики по всему коду.
Как хранить и обрабатывать статусы
Мы уже нарисовали граф состояний конечного автомата — возможные состояния комментария и переходы между ними. В нашем случае разрешены не все переходы: в состояние «на проверке» вернуться нельзя. Это ограничение обусловлено требованием
Каждое состояние конечного автомата должно определяться значением одного свойства, причем значения этого свойства должны быть взаимоисключающими. В разобранном примере в модели данных вместо двух свойств shown и sent нужно ввести одно свойство status с тремя возможными значениями:
$$\usetikzlibrary{arrows,positioning} \begin{tikzpicture}[font=\sffamily] \tikzset{ block/.style={rectangle,rounded corners,draw=black,thick, inner sep=0.7em, text width=8em,text centered}, myarrow/.style={->, >=latex', shorten >=1pt, shorten <=2pt,thick} } \node[block,fill=yellow!10] (moder) {\shortstack{На проверке\\\tt status=pending}}; \node[block, above right=0cm and 3cm of moder,fill=green!10] (pub) {\shortstack{Опубликован\\\tt status=published}}; \node[block, below right=0cm and 3cm of moder,fill=gray!10] (hidden) {\shortstack{Скрыт\\\tt status=hidden}}; \draw[myarrow] (moder) to[in=180,out=30] node[above] {\shortstack{Одобрить\\ (+рассылка)}} (pub); \draw[myarrow] (moder) to[in=180,out=-30] node[below] {Отклонить} (hidden); \draw[myarrow] (pub) to[in=120,out=-120] node[left] {Скрыть} (hidden); \draw[myarrow] (hidden) to[in=-60,out=60] node[right] {Опубликовать} (pub); \end{tikzpicture}$$
После этого везде в коде вместо проверки двух разных свойств shown и sent нужно проверять значение одного свойства status. Например, в запросе для вывода комментариев читателям блога нужно писать не WHERE shown=1, а WHERE status='published'.
Сходу программисту может быть непонятно, какой набор значений должен быть у поля «статус». Но это не значит, что у моделируемых объектов нет набора состояний и возможных переходов между ними. Если их не выявить, код окажется более сложным и запутанным, чем мог бы быть. А если статус выделен правильно, получаем такие преимущества:
- в условных операторах происходит простая проверка статуса, в них нет дополнительных проверок набора свойств;
- добавление новых состояний и переходов упрощается и не требует значительных изменений имеющегося кода;
бизнес-логика прозрачная, состояния моделей и самих моделируемых объектов напрямую соответствуют друг другу.
Польза для общения с бизнесом
Последний пункт имеет отдельную ценность и требует дополнительного объяснения. Важным элементом в разработке проектов является общий язык. Статусы сущностей — это часть общего языка, на котором должны разговаривать не только разработчики, но и заказчики со стороны бизнеса. Не бойтесь использовать статусы при объяснении того, как работает система сейчас и как она будет работать после внесения изменений.
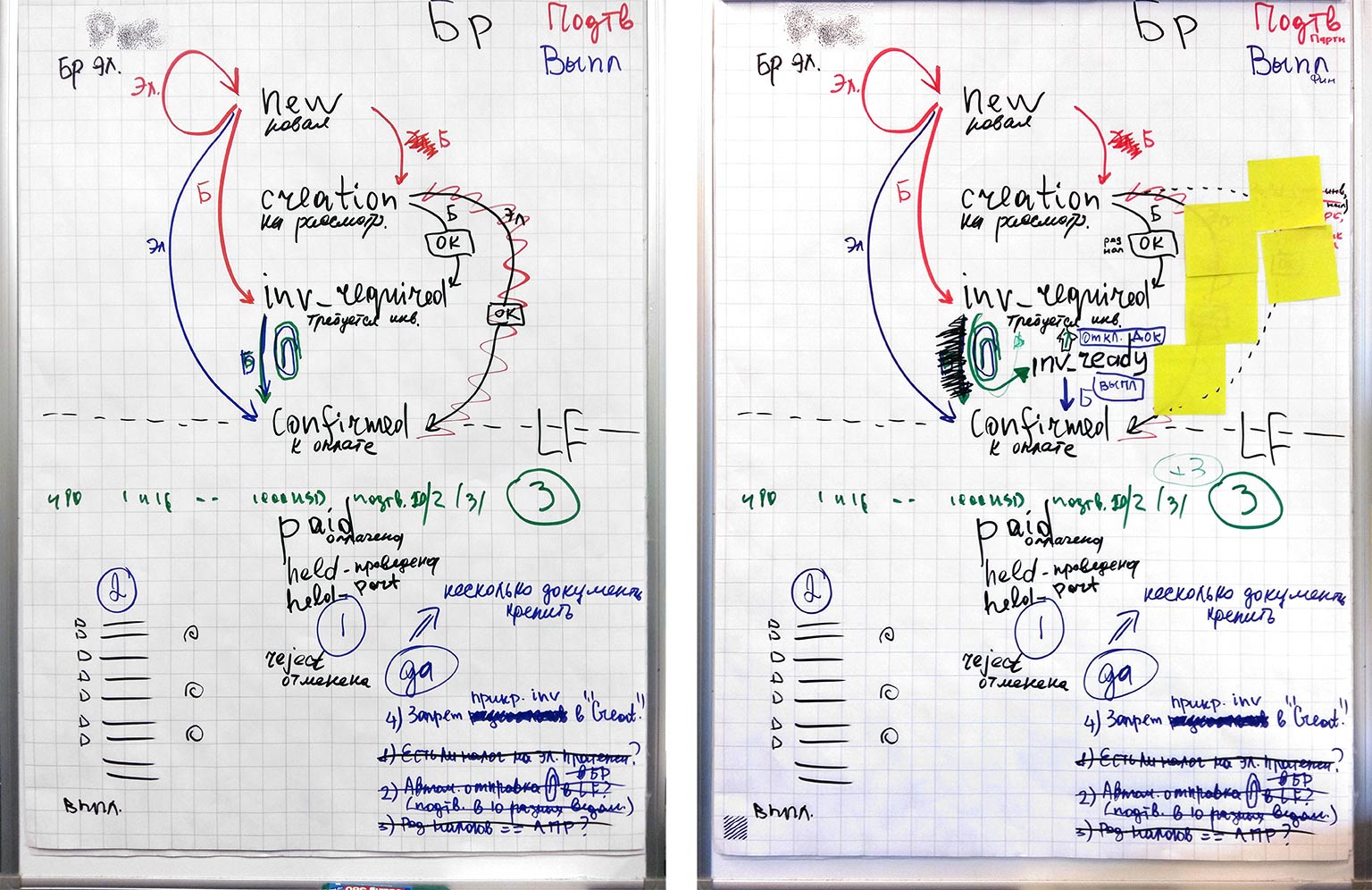
На этой фотографии пример того, как я рисовал конечный автомат заявок на выплаты во время проработки задачи с заказчиком. Видно, что у заявок много статусов, за разные переходы отвечают пользователи с разными ролями. По мере проработки задачи мы поняли, что одного нового статуса мало, нам нужен еще один дополнительный статус.
Состояния в больших системах
В крупных системах невозможно хранить информацию о состоянии обрабатываемых сущностей в одной колонке одной таблицы базы данных, как это было в примере выше.
Для примера представьте, что вы отправляете заявку на ипотечный кредит через личный кабинет на сайте банка. Пока вы заполняете анкету, фотографируете и прикрепляете документы, заявка находится в статусе «черновик». При отправке заявки вы переводите ее в статус «на проверке». Одни сервисы начинают выполнять автоматические проверки. В других сервисах происходит ручная проверка прикрепленных фотографий. Личный кабинет скорее всего не будет знать о таких мельчайших подробностях, как состояние запроса в ФНС на получение вашего ИНН (запрос еще не отправлен, ожидается ответ, ответ получен). Но если в ходе проверки были выявлены проблемы, личный кабинет их отобразит. Например, если паспорт прошел проверку, а справка по форме
Таким образом, за одним значением статуса
Состояния в append-only системах
На первый взгляд кажется, что для сохранения меняющегося статуса нужно делать UPDATE записи в базе данных. Однако это несовместимо с иммутабельными объектами и с логическим продолжением принципа иммутабельности — с таблицами, в которых данные не изменяются, а только дописываются.
В
Зачем вообще делать
- Если записи в таблице никогда не обновляются, не нужно дополнительно программировать и хранить историю изменений. Вся история будет в основных таблицах с данными.
- Базы данных любят, когда данные в таблицах не обновляются, а только дописываются. Например, в PostgreSQL
UPDATE— это на самом деле комбинацияDELETEиINSERT. Удаленные версии строккакое-то время хранятся на диске, их потом нужно дополнительно вычищать. Происходитчто-то вроде фрагментации, когда дисковое пространство используется неэффективно. Кроме того, в огромныхappend-only таблицах на поля вроде времени создания можно повесить эффективный и компактный индекс BRIN. - Не нужно заботиться об инвалидации закешированных строк из базы данных. Например, в кеше второго уровня в Доктрине из коробки лучше всего работает режим READ_ONLY. Инвалидация кеша приложения становится особенно проблематичной в системах с несколькими копиями приложения на разных серверах: когда один сервер делает
UPDATE, другие об этом просто так не узнают и продолжат использовать старую версию из кеша.