Глюки подключения модема и ошибки мышления
Вспомнил историю, которая хорошо иллюстрирует одну из ошибок мышления: «после — не значит вследствие».
Чуть больше 20 лет назад у меня появился первый компьютер. В те времена большинство пользователей интернета выходили туда через модемы — специальные платы, которые позволяли подключать компьютеры к телефонной линии. Чтобы заработал интернет, специальная программа «звонила» по номеру провайдера, и по телефонной линии передавалась цифровая информация, представленная как аудиосигнал.
В компьютере был модем с заявленной скоростью 33,6 килобит в секунду. Такой скорости подключения я никогда не видел. Настоящая скорость была немного ниже, 28,8 или 31,2 килобита в секунду. По тем временам таким интернетом можно было пользоваться
Скорость передачи данных через модем зависит от качества телефонной линии. У меня изредка появлялись ошибки подключения. Я списывал их на плохой контакт в проводе от компьютера к телефонной розетке. Стандартный провод был слишком коротким, и я его удлинил. Когда начинались ошибки подключения, я наклонялся к компьютеру, шевелил провод и разъемы, пытаясь улучшить контакт. После нескольких попыток ошибки пропадали.
Чтобы
В
Вообще, это
Интересно посмотреть, почему я не сразу понял, что причина проблем в кривой прошивке.
Наверно, мы все слышали об этой логической ошибке: после — не значит вследствие. Одно дело — знать о ней, и совсем другое — понять, что мы совершаем ее раз за разом.
Метод удвоения персонажей
Есть известный тип задач по математике, в которых несколько объектов движутся определенным образом,
Откуда появился метод
Однажды коллега дал мне задачу на движение, якобы с собеседований (см. задачу №1 ниже). Чтобы упростить решение, я использовал метод (назовем его «удвоением персонажей»), о котором узнал из книжки Мартина Гарднера «Математические досуги». В ней сформулирована следующая задача:
Теорема о неподвижной точке. Однажды утром, как раз в тот момент, когда взошло солнце, один буддистский монах начал восхождение на высокую гору. Узкая тропа шириной не более
одного-двух футов вилась серпантином по склону горы к сверкающему храму на ее вершине.Монах шел по дорожке с разной скоростью; он часто останавливался, чтобы отдохнуть и поесть сушеных фруктов, которые взял с собой. К храму он подошел незадолго до захода солнца. После нескольких дней поста и размышлений монах пустился в обратный путь по той же тропе. Он вышел на рассвете и опять спускался с неодинаковой скоростью, много раз отдыхая по дороге. Средняя скорость спуска, конечно, превышала среднюю скорость подъема.
Докажите, что на тропе есть такая точка, которую монах во время спуска и во время подъема проходил в одно и то же время суток.
Решение задачи оказалось элегантным:
Человек поднимается на высокую гору и, пробыв несколько дней на вершине, спускается вниз. Найдется ли такая точка на тропе, которую оба раза он проходит в одно и то же время суток? Мое внимание на эту задачу обратил психолог из Орегонского университета Р. Хайман, который в свою очередь нашел ее в монографии, озаглавленной «О решении задач» и принадлежащей перу немецкого психолога Дункера. Дункер пишет, что сам он не смог решить задачу, и с удовлетворением отмечает, что никто из тех, кому он ее предлагал, тоже не добился успеха. Далее Дункер говорит о том, что существует много подходов к решению задачи, но, по его мнению, «самым очевидным является следующее объяснение. Пусть в один и тот же день по тропе идут два человека: один из них поднимается вверх, а второй спускается вниз. Они обязательно должны встретиться. Отсюда, как вы сами понимаете, следует, что… при таком подходе неясный вначале смысл задачи вдруг сразу становится совершенно очевидным».
Понятно, что в большинстве задач на движение за счет идеализации нет запутывающих сложностей: объекты движутся с постоянной скоростью, не тратят время на остановки и развороты. Но даже тогда приемы вроде перехода от ситуации с одним монахом к ситуации с двумя монахами упрощают рассуждения. Давайте посмотрим на примерах, как работает такой метод.
Задача №1
Человек хочет пройти через туннель для поездов. Пройдя четверть пути, он слышит приближающийся сзади поезд. Скорость поезда и расстояние до него неизвестны. Если человек развернется и побежит назад, то он достигнет начала туннеля одновременно с поездом. Если же человек побежит вперед, то конца туннеля он также достигнет одновременно с поездом. На сколько быстрее движется поезд по сравнению с человеком?
Решение через систему уравнений
Давайте для сравнения сначала решим задачу школьными методами.
Пусть скорость человека есть v, скорость поезда u, расстояние от поезда до тоннеля x, длина тоннеля y. В первой ситуации пока поезд проходит расстояние x до начала тоннеля, человек пробегает назад четверть y. Приравняем времена этих движений:
$${x\over u}={y/4\over v}.$$
Во второй ситуации до встречи поезд проходит сумму расстояний x и y, человек пробегает три четверти y. Аналогично получаем:
$${x+y\over u}={3y/4\over v}.$$
Вычитаем из второго уравнения первое:
$${y\over u}={2y/4\over v}={y\over 2v}.$$
Переменная x исчезла, у как ненулевая величина сокращается. Отсюда $$u=2v$$, то есть поезд в два раза быстрее.
Решение методом удвоения персонажей
Предположим, что через тоннель идет не один человек, а два. В момент обнаружения поезда первый бежит к началу тоннеля, а второй к концу.
$$\begin{tikzpicture}[font=\sffamily,scale=1.0545,line width=0.2mm] \node[fill=green!20] (1) at (1.5,0.5) {1}; \node[fill=blue!20] (2) at (1.5,1) {2}; \draw[->] (1.west) -- ++(-0.5,0); \draw[->] (2.east) -- ++(0.5,0); \node[fill=red!30] at (-4,-0.5) {поезд}; \draw[semithick] (-5,0) -- (8,0); \foreach \x in {0,1.5,3,4.5,6} \draw (\x,0.14) -- (\x,-0.14); \draw[fill=yellow] (0,-0.04) rectangle ++(6,0.08); \draw [opacity=0] (-5,-0.76) rectangle (8.0,1.24); \end{tikzpicture}$$
Когда первый пробежал четверть тоннеля и добежал до его начала, второй тоже пробежал четверть и оказался в середине тоннеля. В этот момент поезд проезжает начало тоннеля.
$$\begin{tikzpicture}[font=\sffamily,scale=1.0545,line width=0.2mm] \node[fill=green!20] at (0,0.5) {1}; \node[fill=blue!20] at (3,0.5) {2}; \node[fill=red!30] at (0,-0.5) {поезд}; \draw[semithick] (-5,0) -- (8,0); \foreach \x in {0,1.5,3,4.5,6} \draw (\x,0.14) -- (\x,-0.14); \draw[fill=yellow] (0,-0.04) rectangle ++(6,0.08); \draw [opacity=0] (-5,-0.76) rectangle (8.0,1.24); \end{tikzpicture}$$
Второму осталось бежать расстояние от середины тоннеля до конца, а поезду — проехать от начала тоннеля и до конца. По условию они делают это за одинаковое время.
$$\begin{tikzpicture}[font=\sffamily,scale=1.0545,line width=0.2mm] \node[fill=green!20] at (0,0.5) {1}; \node[fill=blue!20] at (6,0.5) {2}; \node[fill=red!30] at (6,-0.5) {поезд}; \draw[semithick] (-5,0) -- (8,0); \foreach \x in {0,1.5,3,4.5,6} \draw (\x,0.14) -- (\x,-0.14); \draw[fill=yellow] (0,-0.04) rectangle ++(6,0.08); \draw [opacity=0] (-5,-0.76) rectangle (8.0,1.24); \end{tikzpicture}$$
Таким образом, поезд в два раза быстрее человека.
Сравнение методов
Ясно, что оба метода по своему смыслу одинаковы. Но рассуждения во втором методе не только наглядны, но и выстроены в одну линию. Ход рассуждений и временной ход событий из задачи совпадают. Поэтому при решении не нужно держать в голове сведения из всей задачи целиком, можно последовательно перебирать происходящие события.
Задача №2
Велосипедист едет вдоль железной дороги. Он заметил, что электрички, которые идут в ту же сторону, обгоняют его с интервалом в час, а электрички, которые идут в обратную сторону, встречаются ему с интервалом в полчаса. С каким интервалом электрички выходят с конечных станций?
Эту задачу разбирали в следующем ролике на канале GetAClass:
Давайте посмотрим, как применить в этой задаче метод удвоения персонажей.
Решение
В этой задаче нас путают электрички, которые едут в двух разных направлениях. Перейдем к эквивалентной задаче, в которой электрички едут только в одном направлении, но велосипедистов два. Первый, который едет по ходу движения электричек, встречает их раз в час, а второй — в противоположном направлении — раз в полчаса.
Пусть в начальный момент времени электричка и два велосипедиста находятся в одной точке.
$$\begin{tikzpicture}[font=\sffamily,scale=1.0545,line width=0.2mm] \node[fill=green!20] (1) at (2,0.5) {1}; \node[fill=blue!20] (2) at (2,1) {2}; \draw[->] (1.east) -- ++(0.5,0); \draw[->] (2.west) -- ++(-0.5,0); \node[fill=red!30] at (2,-0.5) {электричка 1}; \draw[-,semithick] (-5,0) -- (8,0); \foreach \x in {0,2,4,6} \draw (\x,0.1) -- (\x,-0.1); \draw [opacity=0] (-5,-0.8) rectangle (8.0,1.24); \end{tikzpicture}$$
Через полчаса второй велосипедист, едущий назад, встречает следующую электричку. Запомним, что к этому моменту первый велосипедист проехал полчаса вперед. То есть расстояние между велосипедистами соответствует часу проходимого ими пути, назовем его
$$\begin{tikzpicture}[font=\sffamily,scale=1.0545,line width=0.2mm] \node[fill=green!20] at (4,0.5) {1}; \node[fill=blue!20] at (0,0.5) {2}; \node[fill=red!30] at (0,-0.5) {электричка 2}; \draw[-,semithick] (-5,0) -- (8,0); \foreach \x in {0,2,4,6} \draw (\x,0.1) -- (\x,-0.1); \draw [opacity=0] (-5,-0.8) rectangle (8.0,1.24); \end{tikzpicture}$$
За следующие полчаса электричка проезжает этот
$$\begin{tikzpicture}[font=\sffamily,scale=1.0545,line width=0.2mm] \node[fill=green!20] at (6,0.5) {1}; \node[fill=blue!20] at (-2,0.5) {2}; \node[fill=red!30] at (6,-0.5) {электричка 2}; \draw[-,semithick] (-5,0) -- (8,0); \foreach \x in {0,2,4,6} \draw (\x,0.1) -- (\x,-0.1); \draw [opacity=0] (-5,-0.8) rectangle (8.0,1.24); \end{tikzpicture}$$
Теперь мы видим, что за последние полчаса электричка проезжает расстояние, в три раза большее, чем велосипедист, $$u=3v$$.
До второй половины решения задачи не так легко додуматься. Попробую объяснить, как к нему прийти. В условии есть некоторая неизменная величина — расстояние между соседними электричками. С ней проще работать в той системе отсчета, где электрички покоятся. То есть мы сейчас посмотрим на события глазами пассажиров электрички. Первый велосипедист движется в ту же сторону, что и мы, но мы в три раза быстрее. Скорость, с которой мы догоняем велосипедиста, равна двум велосипедным. Второй велосипедист движется на нас, и скорость сближения равна четырем велосипедным. К пассажирам на неподвижных станциях мы приближаемся с собственной скоростью, равной трем велосипедным скоростям. Нам будет казаться, что с этой скоростью они проносятся мимо нас назад. Получается, что одно и то же расстояние S между нами и следующей за нами электричкой первый велосипедист проходит с относительной скоростью 2v за час, второй с относительной скоростью 4v проходит за полчаса, а пассажиры на станции со скоростью 3v «преодолевают» за искомое время t. Запишем в виде уравнений:
$$S=2v\cdot 1,\quad S=4v\cdot{1\over 2},\quad S=3v\cdot t.$$
То, что первое и второе уравнения получились одинаковыми, показывает, что в первой половине решения ошибок не было. Из этих уравнений видно, что $$t=2/3$$ часа, или 40 минут.
Я бы не сказал, что до этого решения задачи додуматься проще всего. Можно было сразу записать систему уравнений с неизвестными скоростями $$(u-v)\cdot 1=(u+v)\cdot 0,\!5=u\cdot t$$ и решить ее относительно t. Но мне надо было на
Некоторые возможности регулярных выражений, о которых мало кто знает
На примере задачи с поиском определенных последовательностей символов в строке расскажу о некоторых не очень известных возможностях регулярных выражений.
Условие задачи
Нужно найти в строке символы i, b, u, d, перед которыми расположено нечетное количество обратных слешей, например \I или \\\b.
Мотивация
Расскажу, откуда появилась эта задача. В свой поисковый движок Rose я добавил поддержку простейшего форматирования в сниппетах: курсив, жирный шрифт, верхние и нижние индексы. Благодаря этому формула
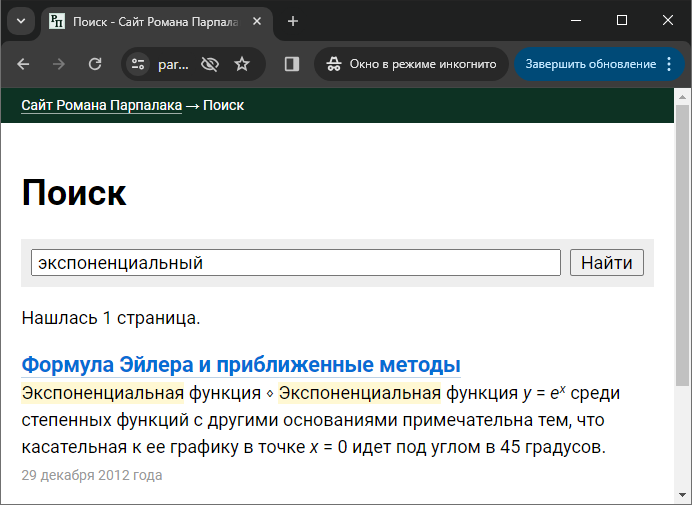
Я не хотел хранить текст сниппетов с частично вырезанными \i включает курсивное начертание, последовательность \I отключает. Аналогично с остальным форматированием. При этом, чтобы хранить сам символ обратного слеша, его нужно продублировать для экранировки (\\). Таким образом, формула из примера выше хранится в сниппетах как \iy\I = e\u\ix\I\U.
Как видно на скриншоте выше, сниппеты собираются из отдельных предложений, а форматирование может распространяться за их границы. Например, я могу выделить курсивом целый абзац, тогда \i будет в начале первого предложения, а \I — в конце последнего. Поэтому важно после разбиения текста на предложения убедиться, что всё открытое форматирование корректно завершено в текущем предложении и перенесено на следующее, и нет завершения неоткрытого форматирования. Для этого как раз и нужна сформулированная задача.
Решение
Я составил такую регулярку: #\\(?:\\(*SKIP)\\)*\K[ibud]#i. Давайте разберем ее по шагам.
- Регулярка начинается с символа обратного слеша. Нужно помнить, что в регулярных выражениях он имеет специальное значение, и сам по себе должен быть экранирован.
- Дальше идет группа
(?:...)без захвата, то есть ее содержимое не попадает в итоговый массив результатов$matches. - Внутри группы находятся два обратных слеша, а сама группа указана с
квантификатором , означающим её повторение любого количества раз, включая нулевое. Таким образом уже разобранная часть регулярки должна срабатывать на нечетном количестве слешей.* - Внутри группы также расположена управляющая последовательность бэктрекинга
(*SKIP). Она обозначает некоторую границу и дает инструкции движку регулярных выражений, чтобы он не переходил эту границу при переборе возможных повторений, задаваемыхквантификатором , а также сразу переходил к ней в исходной строке, если было только частичное совпадение с регуляркой. Без этой управляющей последовательности мы бы получили ложное совпадение на строке*\\iс четным количеством слешей. Действительно, в ней на первом проходе, начиная с первого символа\\i, совпадения нетиз-за четного количества слешей. Но дальше мы получим совпадение, начиная со второго символа:\\i.(*SKIP)же задает границу между вторым слешем и следующим символом, поэтому движок регулярок при работе не будет проверять совпадение со второго символа, а сразу перейдет к третьему. В англоязычной литературе для подобных управляющих последовательностей используется термин Backtracking Control Verbs, среди них есть и другие полезные возможности. - Следующей идет последовательность
\K. Она убирает из результатов общего совпадения всё, что было до нее. Таким образом, в$matches[0]попадет только оставшаяся часть совпадения, без слешей. - Наконец, мы требуем, чтобы после нечетного количества слешей был один из управляющих символов
[ibud]. Так как у регулярки указан модификаторi, совпадение будет в любом регистре.
Если не использовать жемчужину этой регулярки, (*SKIP), можно сочинить выражение с ретроспективной проверкой (lookbehind): #(?<=^|[^\\])\\(?:\\\\)*\K[ibud]#i. Правда, оно будет менее эффективно на строках с обратным слешем. Ну а наивное выражение #(?:^|[^\\])\\(?:\\\\)*\K[ibud]#i будет медленнее на любых строках, так как не начинается с фиксированного символа обратного слеша.
При применении регулярных выражений не нужно забывать о дополнительном экранировании слешей по требованиям синтаксиса языка программирования. Итоговый код на PHP получается таким:
preg_match_all('#\\\\(?:\\\\(*SKIP)\\\\)*\K[ibud]#i', $text, $matches);
foreach ($matches[0] as $match) {
// в $match будет один из символов ibudIBUD
}Codeium — нейросетевой помощник программиста
Попробовал в работе Codeium — нейросетевой помощник в написании кода. Его обзор уже был на хабре, так что я просто запишу свои наблюдения, не претендуя на полноту рассмотрения.
Как работает Codeium
Я установил его как плагин к PhpStorm. Для работы он требует войти в аккаунт, но регистрация бесплатна.
Пользователь взаимодействует с плагином двумя способами. Первый — автодополнение. Вы набираете код, останавливаетесь, и в этот момент нейросеть выдает возможное продолжение. Вот я написал название метода, остановился в начале пустого тела, и Codeium вывел серым предполагаемое начало кода:
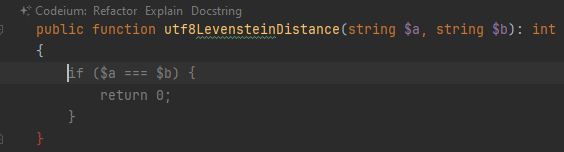
После нажатия на tab и перевода строки нейросеть продолжает сочинять. Вот тут одним махом предлагает написать весь оставшийся код метода:
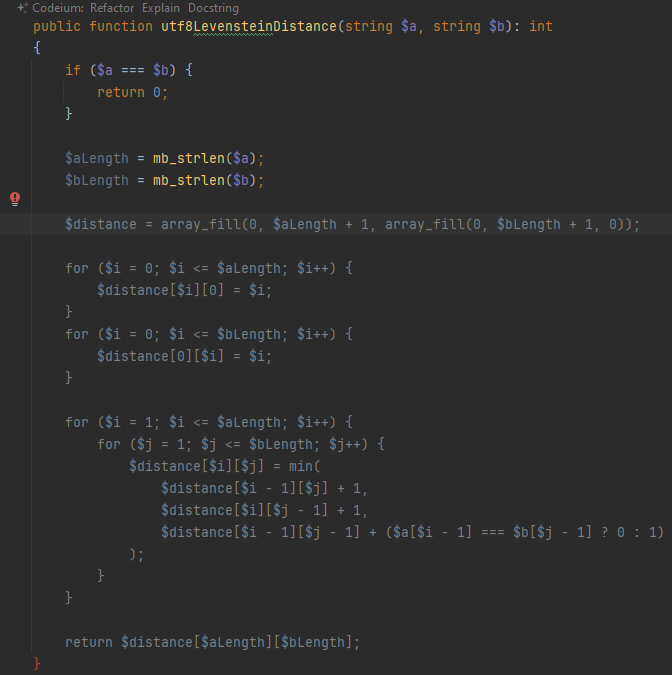
Нейросеть «поняла» из названия метода, что мне нужна версия алгоритма для вычисления расстояния Левенштейна между строками, корректно работающая с кодировкой levenshtein(), но она правильно работает только для однобайтных кодировок). Идея алгоритма оказалась правильной, но с деталями не вышло: сравнение $a[$i - 1] === $b[$j - 1] берет не символы с соответствующими номерами, а байты. После исправления этого фрагмента на mb_substr($a, $i - 1, 1) === mb_substr($b, $j - 1, 1) код заработал правильно.
Второй способ взаимодействия — это чат. Он мне показался туповатым по сравнению с ChatGPT. Я так и не понял, лучше ли работают английские запросы, или можно писать
Главный вау-эффект
Наибольшая помощь от «искусственного интеллекта» была в переписывании кода и конфигурации из одного формата в другой. Допустим, вы меняете формат
Недостатки
Теперь о недостатках, куда же без них.
Ненативность автодополнения проявляется еще, например, при переименовании. Вот здесь я переименовываю метод так, что PhpStorm заменит его вызовы по всему проекту. На этот режим указывает голубая рамка. Codeium умудряется дописать свое мнение еще и сюда, но сам PhpStorm о нем ничего не знает. Когда я применил подсказку пару недель назад и закончил переименовывать, PhpStorm заменил вызовы по всему проекту на недополненное несуществующее название. Сейчас при попытке воспроизведения tab в режиме переименования просто не работает, подсказка не применяется. То есть Codeium выдает свой вариант, но применить его никак нельзя.
По внешнему виду автодополнения непонятно, что это предложение помощника. Просто серый текст, неотличимый от комментария. В
Еще одна особенность текущего механизма взаимодействия: нет возможности оставить часть предложенного автодополнения, скажем, первые несколько слов. Можно только принять всё целиком и удалить лишнее.
Вывод
В процессе работы перевешивают то достоинства нейросетевого помощника, то его недостатки. Забавно наблюдать, как нейросеть «читает» твои мысли, выдавая ровно тот код, который ты сам собрался написать. Правда, происходит такое не всегда. Когда нейросеть предлагает нужные фрагменты кода, их надо тщательно проверить, как за
В общем, перспективы большие. Пользовательский опыт сейчас страдает. Пробуйте сами.
Да, и не забывайте о вопросах безопасности. Наверняка Codeium отправляет всё редактируемое на свои серверы. Я пробовал его на открытом опубликованном коде своего движка, так что дополнительно ничего «утечь» не может. Если хотите попробовать на работе — проконсультируйтесь с вашим отделом по информационной безопасности.
Тесты выявляют проблемы не только с вашим кодом
Удивительные тесты
Представьте, что вы пришли на новый проект и обнаружили в нем вот такой тест:
<?php
use Codeception\Test\Unit;
class MyTest extends Unit
{
public function testHash(): void
{
$this->assertEquals('098f6bcd4621d373cade4e832627b4f6', md5('test'));
}
}
Для неспециалистов поясню, что этот тест вызывает встроенную в PHP функцию md5(), передает ей аргумент 'test' и проверяет, что она возвращает указанное значение.
Зачем нужен этот тест, если встроенная функция и так вычисляет хеш по известному задокументированному алгоритму? Мы же пишем тесты на наш проект, а не на интерпретатор PHP. Написавший этот тест коллега на вопросы отвечает так:
— В наших алгоритмах мы полагаемся на значения хешей, сохраненные в базе данных. Если вдруг функция начнет возвращать другие значения в будущих версиях PHP, мы заметим это по упавшему тесту. Конечно, такие изменения нарушают обратную совместимость, и они должны быть написаны в информации о релизе PHP. Но их можно просмотреть
Как считаете, писать в проекте тест на встроенную функцию PHP — это паранойя? Или разумная предусмотрительность? А что, если это не встроенная функция в PHP, а сторонняя библиотека? Правда же, такой тест вызывает меньше удивления:
<?php
use Codeception\Test\Unit;
use SuperVendor\SuperHashLib\SuperHash;
class MyTest extends Unit
{
public function testHash(): void
{
$this->assertEquals('098f6bcd4621d373cade4e832627b4f6', SuperHash::getHash('test'));
}
}
Тест выявил изменение поведения при обновлении PHP
В моей практике похожий тест действительно однажды помог отследить вредный побочный эффект от нарушения обратной совместимости при обновлении PHP. Минимальный пример для воспроизведения такой:
<?php
class A
{
public $prop1 = '1';
public $prop2 = '2';
public function getHash(): string
{
return md5(serialize($this->normalize()));
}
public function normalize(): array
{
return get_object_vars($this);
}
}
class B extends A
{
public $prop3 = '3';
}
$a = new A;
var_dump($a->getHash());
$b = new B;
var_dump($b->getHash());
Этот код в старых версиях PHP до 8.1 выводит следущее:
string(32) "e5f8d9c52536e3412aa273c7bd4c9dbb"
string(32) "46d9b1133eec8d47fe6e00e970cf0a77"А начиная с 8.1 значение хеша у объекта класса B изменилось:
string(32) "e5f8d9c52536e3412aa273c7bd4c9dbb"
string(32) "8275b764cf277cbbd3b00b1e86d8a4eb"Причина различий в изменении порядка свойств в массиве, возвращаемом get_object_vars(). В старых версиях сначала шли свойства самого класса, а затем унаследованные от родительского:
// До PHP 8.1
Array
(
[prop3] => 3
[prop1] => 1
[prop2] => 2
)В новых же версиях сначала идут унаследованные свойства, а потом собственные свойства класса:
// PHP 8.1 и старше
Array
(
[prop1] => 1
[prop2] => 2
[prop3] => 3
)Как видите, такое изменение поведения при обновлении PHP меняет значения хешей, вычисляемые очевидным и прямолинейным способом. И это изменение даже не было заявлено в информации о релизе как ломающее обратную совместимость!
Мы смогли отловить проблему как раз благодаря тесту, в котором проверялось точное значение вычисленного хеша. Правда, он был написан с другой целью. В нашем случае при добавлении новых полей мы исключали их из вычисления хеша, чтобы хеш не менялся, если новые поля не используются:
<?php
class A
{
public $prop1 = '1';
public $prop2 = '2';
public $propN = null;
public function getHash(): string
{
return md5(serialize($this->normalize()));
}
private function normalize(): array
{
$data = get_object_vars($this);
if ($this->propN === null) {
unset($data['propN']);
}
return $data;
}
}Чтобы разработчики не забывали добавлять unset() новых
Пример решения проблем с обратной совместимостью алгоритмов хеширования
Чтобы дважды не вставать и рассказать не только о проблеме, но и о том, как ее решать, рассмотрим пример, в котором требуется подход с get_object_vars() и вычислением хешей.
Предположим, вы разрабатываете сервис для отслеживания цен на товары в
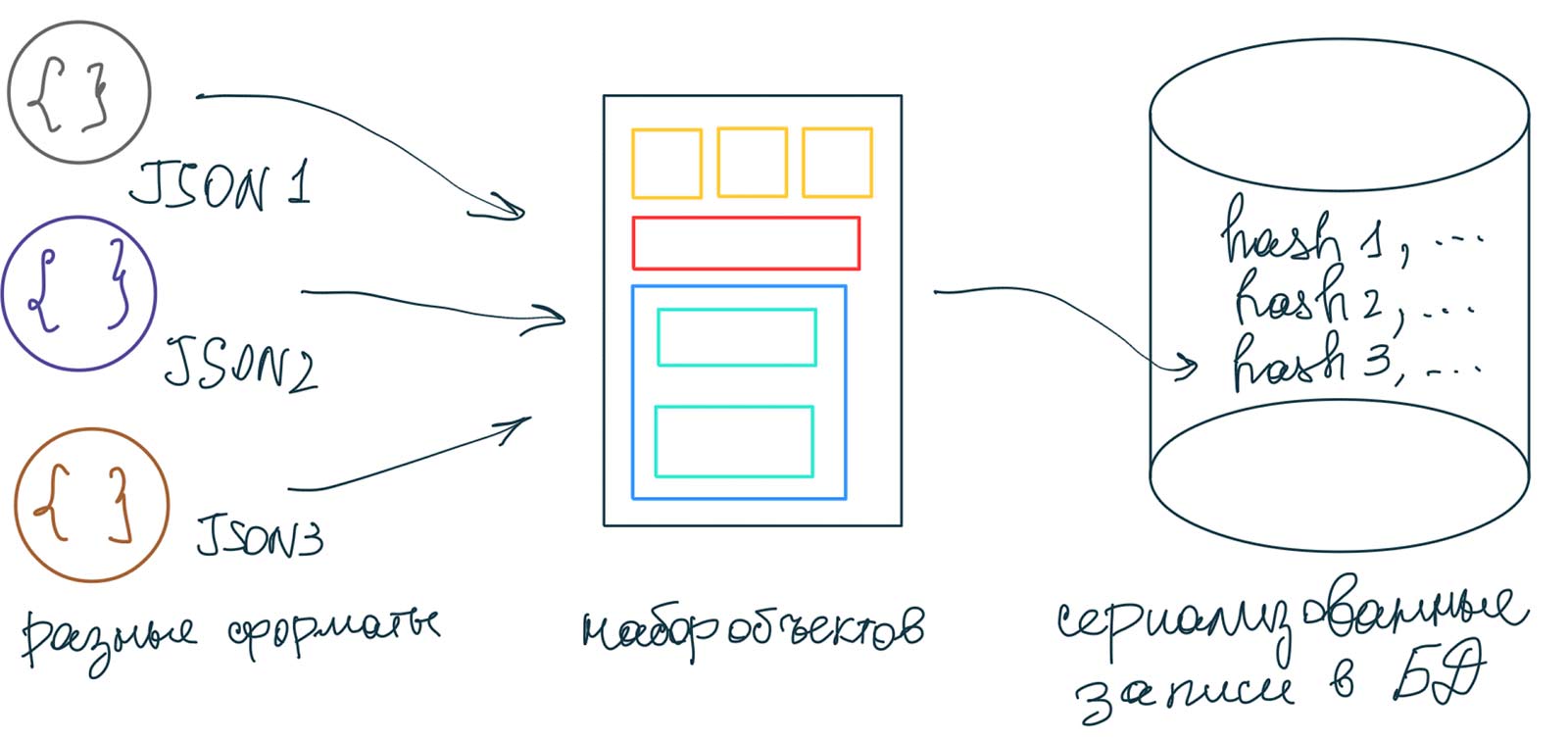
На входе у вас множество источников данных из разных products:
| id | hash | data |
|---|---|---|
| 1001 | e5f8d9c52… | {"color":"red"…} |
| 1002 | 8275b764c… | {"color":"green"…} |
После этого для записи истории цен достаточно вести таблицу price_history:
| product_id | date | price |
|---|---|---|
| 1001 | 1099,9 | |
| 1001 | 1199,9 |
Если в источниках данных появляется новый товар или новая модификация известного товара, метод getHash() вернет неизвестное ранее значение, и в таблицу products добавится новая запись. Если товар ранее уже встречался, значение getHash() уже будет присутствовать в таблице products, и значение для product_id берется из соответствующей записи.
Теперь мы видим, к каким последствиям может привести изменение в алгоритме вычисления хешей. product_id. Вы потратите много времени и сил, пытаясь сначала найти причину проблем, а потом исправлять данные в БД, изменяя идентификаторы и подчищая дубликаты.
Как же решать проблему с изменением алгоритма хеширования? Примерно так же, как изменяется тип колонок в огромных таблицах БД. Для начала напишем новый метод вычисления хеша, инвариантный относительно изменения порядка свойств:
public function getHash2(): string
{
$data = $this->normalize();
ksort($data);
return md5(serialize($data));
}
Далее делаем в таблице БД новую колонку со значением нового хеша. При поиске записей в этой таблице по хешу нужно сначала искать по новой версии хеша, а затем, если ничего не нашли, по старой версии. При добавлении новых записей пока будем записывать значения и новой колонки, и старой. Старые значения хеша всё еще требуются для возможного отката.
После успешной выкладки, если откат не нужен, надо обновить значения новой колонки у старых записей. Это сделает отдельный скрипт, который прочитает все записи, переведет данные в объекты, по объектам посчитает новую версию хешей и выполнит UPDATE.
В завершение можно выкладывать окончательную версию кода, в которой останется только новая версия алгоритма хеширования, и запускать миграцию, которая удалит колонку со старыми версиями хешей.
Вывод
Обычно, когда программист пишет тесты к разрабатываемому приложению, он ориентируется на выполняемые приложением функции. В нашем примере приложение собирает цены из нескольких источников и выводит на странице. Тогда и в тесте сначала импортируется несколько файлов с данными, а затем проверяется, что эти данные выводятся корректно. Это будет означать, что вся цепочка преобразования данных отработала правильно.
Кроме функций приложения, нужно задуматься еще о том, какие предположения делаются в ходе разработки. И эти предположения тоже можно проверять в тестах. Мы разобрали один из примеров, когда предполагалось, что одинаковые данные на входе дадут одинаковые значения хешей. Если забыть о неявном требовании, что хеши не должны меняться со временем (они сравниваются с записанными значениями в БД), легко написать тесты на саму функцию, которые не упадут при изменении алгоритма хеширования. И вы отправите проблемные изменения в рабочую систему, будучи уверенными, что всё в порядке, так как тесты пройдены.
Мониторинг доступности сайтов в UptimeRobot
Уже три года для мониторинга доступности своих сайтов я использую сервис UptimeRobot. Он ходит по вашим ссылкам с указанным интервалом и проверяет статусы ответа и наличие в нем определенных ключевых слов. Конечно, это не полноценная проверка работоспособности сайтов, но проблемы вроде неоплаченного домена или хостинга она способна выявить.
На бесплатном тарифе есть ограничение — не больше 50 проверок, интервал не чаще чем раз в 5 минут.
Я подумал, что неплохо бы на моем сервисе генерации картинок с математическими формулами разместить информацию об аптайме, чтобы подтвердить фактами его надежность. UptimeRobot дает API, и я уже было хотел написать интеграцию и отображать данные в
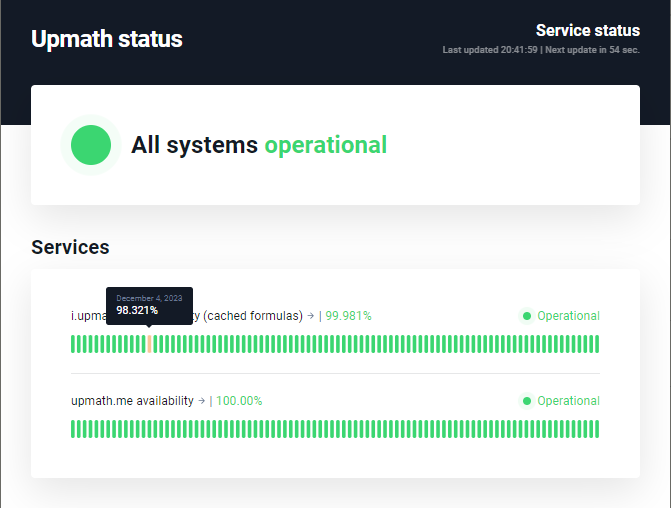
В итоге я просто разместил ссылку на эту страницу, ничего программировать не пришлось. Кому интересно — пройдут и посмотрят. Данные выводятся по дням за последние 3 месяца, без выбора периода. Но зато они отображаются на домене мониторинга, так что вопросов к их объективности нет. Конечно, эту фичу со страницами статусов могут сломать или отключить. Но и API тоже могут отключить, и это было бы даже обиднее, если бы я потратил время на интеграцию.
Пока писал пост, подумал, что у UptimeRobot может быть реферальная программа. Такая программа оказалась, и я разместил реферальную ссылку. Хотя не думаю, что
Как правильно представлять и обрабатывать состояние фильтров в коде
Фильтры в интерфейсах
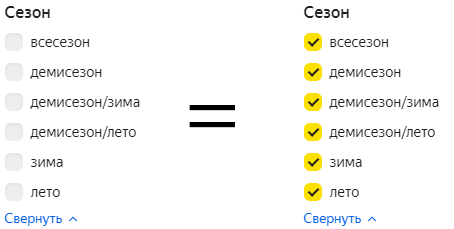
Если рассуждать с точки зрения формальной логики, пустому фильтру нужно было бы сопоставить пустой результат. Но на практике в этом нет смысла. Об этом как раз сегодняшний совет Бюро.
Я хочу рассказать, как правильно обрабатывать в коде эту особенность фильтров. Вообще естественно сопоставить выбранным элементам фильтра элементы массива. В этом случае пустому фильтру будет соответствовать пустой массив. Если мы напишем код из этого предположения, то по всей цепочке передачи состояния фильтра нужно отдельной логикой обрабатывать пустой массив, а это будет громоздко и некрасиво.
Чтобы показать, в чем недостатки кодирования пустого фильтра пустым массивом, рассмотрим типовую операцию — пересечение фильтров. Она требуется, когда мы проверяем права доступа пользователя к выбранным в фильтре элементам. Для иллюстрации представим, что в примере выше есть скрытые сезоны, а в них — скрытые товары. Допустим, мы не хотим продавать летом зимние товары, потому что их нет на складе, и скрываем до следующей зимы. Логика в коде может быть примерно такой:
$filterValues = $request->get('seasons');
$allowedValues = getActiveSeasons();
if ($filterValues === []) {
// В фильтре ничего не выбрано - используем все доступные значения
$intersectValues = $allowedValues;
} else {
$intersectValues = array_intersect($allowedValues, $filterValues);
}
// Получаем список товаров из БД
$result = getProductsByConditions(['seasons' => $intersectValues]);
Мы видим недостаток: $allowedValues и $filterValues обрабатываются несимметрично в этом коде. Пустой массив в $filterValues не приводит к ограничениям списка товаров. А пустой массив в $allowedValues должен приводить к пустому результату. Было бы неправильно отображать товары из всех категорий, после того как я скрыл последнюю доступную категорию.
Представьте теперь, что нам поступило новое требование: администратор должен видеть скрытые товары. Тогда код еще больше усложнится и станет примерно таким:
$filterValues = $request->get('seasons');
$allowedValues = getActiveSeasons();
$conditions = [];
if (grantedHiddenProducts($currentUser)) {
if (!$filterValues === []) {
// Админу фильтруем, только если он сам заполнил фильтр
$conditions = ['seasons' => $filterValues];
}
} elseif ($filterValues === []) {
// В фильтре ничего не выбрано - используем все доступные значения
$conditions = ['seasons' => $allowedValues];
} else {
$intersectValues = array_intersect($allowedValues, $filterValues);
$conditions = ['seasons' => $intersectValues];
}
// Получаем список товаров из БД
$result = getProductsByConditions($conditions);
Я предлагаю интерпретировать значения null. В этом случае множество элементов массива всегда соответствует множеству разрешенных элементов, а null соответствует универсальному множеству — дополнению к пустому множеству.
Если следовать соглашению о кодировке отсутствия ограничений через null, пустой интерфейсный фильтр конвертируется в null в самом начале потока данных. В конце потока при формировании запроса к БД значение null в фильтре игнорируется и в array_intersect() как раз может вернуть пустой массив, если
$filterValues = $request->get('seasons');
if ($filterValues === []) {
// По бизнес-логике если фильтр не выбран, показываем все доступные товары
$filterValues = null;
}
// Скрытые товары показываем только админам
$allowedValues = grantedHiddenProducts($currentUser) ? null : getActiveSeasons();
// Комбинируем ограничения
$intersectValues = array_intersect_sets($allowedValues, $filterValues);
// Получаем список товаров из БД
$result = getProductsByConditions(['seasons' => $intersectValues]);
// ...
function array_intersect_sets(?array $a, ?array $b): ?array {
if ($a === null) {
return $b;
}
if ($b === null) {
return $a;
}
return array_intersect($a, $b);
}
function getProductsByConditions(array $conditions): array {
// ...
if ($conditions['seasons'] !== null) {
if ($conditions['seasons'] === []) {
return [];
}
$queryBuilder->andWhere('p.seasons IN (?)', $conditions['seasons']);
}
// ...
}
В этом варианте в каждом фрагменте кода прозрачная и ясная логика. Функция array_intersect_sets() является симметричной по отношению к перестановке аргументов. Она переиспользуется везде, где нужно применять несколько ограничений одновременно. Из кода пропала проблемная длинная цепочка условных операторов. Раньше при изменении логики фильтрации программист должен был осознать эту цепочку целиком и быть очень внимательным, чтобы не упустить
ChatGPT подсказал название задачи по формулировке
Недавно встретил редкую задачу из теории вероятностей. Сначала сам решил, потом стал спрашивать у ChatGPT, чтобы понять, под каким названием эта задача может быть известна.
Пусть имеется множество из N элементов. В ходе одного испытания случайным образом выбираетсякакой-либо элемент. Сколько в среднем нужно испытаний, чтобы каждый элемент множества был выбран хотя бы один раз?
ChatGPT в целом правильно воспроизводил идею решения, но с названием не заладилось. За несколько попыток правильного названия он так и не выдал, в каждой попытке
Это классическая задача, известная как проблема дней рождения или задача выбора.
Это задача из теории вероятностей, известная как задача о парадоксе дней рождения или проблема обеспечения. В вашем случае, вы спрашиваете о среднем количестве испытаний, необходимых для того, чтобы выбрать каждый элемент множества хотя бы один раз. Это связано с так называемой задачей о шарах и ящиках.
Эта задача относится к классу задач под названием «задача об абсолютной перестановке» или «задача о деньгах дней рождения».
Этот вопрос относится к теории вероятностей и известен как проблема «парадокса дней рождений» или «проблема встречи». В вашем случае, это известно как проблема «выборки с возвратом» (sampling with replacement).
Этот вопрос связан с математической областью, называемой «парадоксом дней рождения» или «задачей о шарах и корзинах». Для вашего вопроса это называется «парадоксом выбора с возвращением».
Когда я добавил к своему запросу «ответ дай
This problem is a classic example of the coupon collector's problem.
Оказывается, эта интересная задача встречается в английской литературе под таким названием, что можно перевести как «задача коллекционера», а в русской литературе практически неизвестна. Я думал, что для ChatGPT не проблема дать ответ с учетом перевода. Но, видимо, при генерации ответа связь между словами одного языка сильнее, чем связи между терминами с учетом перевода.
О самой задаче коллекционера написал подробнее в «черновиках физика».
Как не пропускать прием лекарств
Недавно Экслер рассказал у себя в блоге о способе не пропускать прием лекарств в течение дня. Утром он кладет баночку с витаминами на рабочем месте слева, а по мере приема перекладывает всё правее и правее.
Я в свое время придумал другой способ. На упаковке с лекарством я прямо подписываю дни недели, в которые надо выпить конкретные таблетки. Сама упаковка становится наглядным индикатором
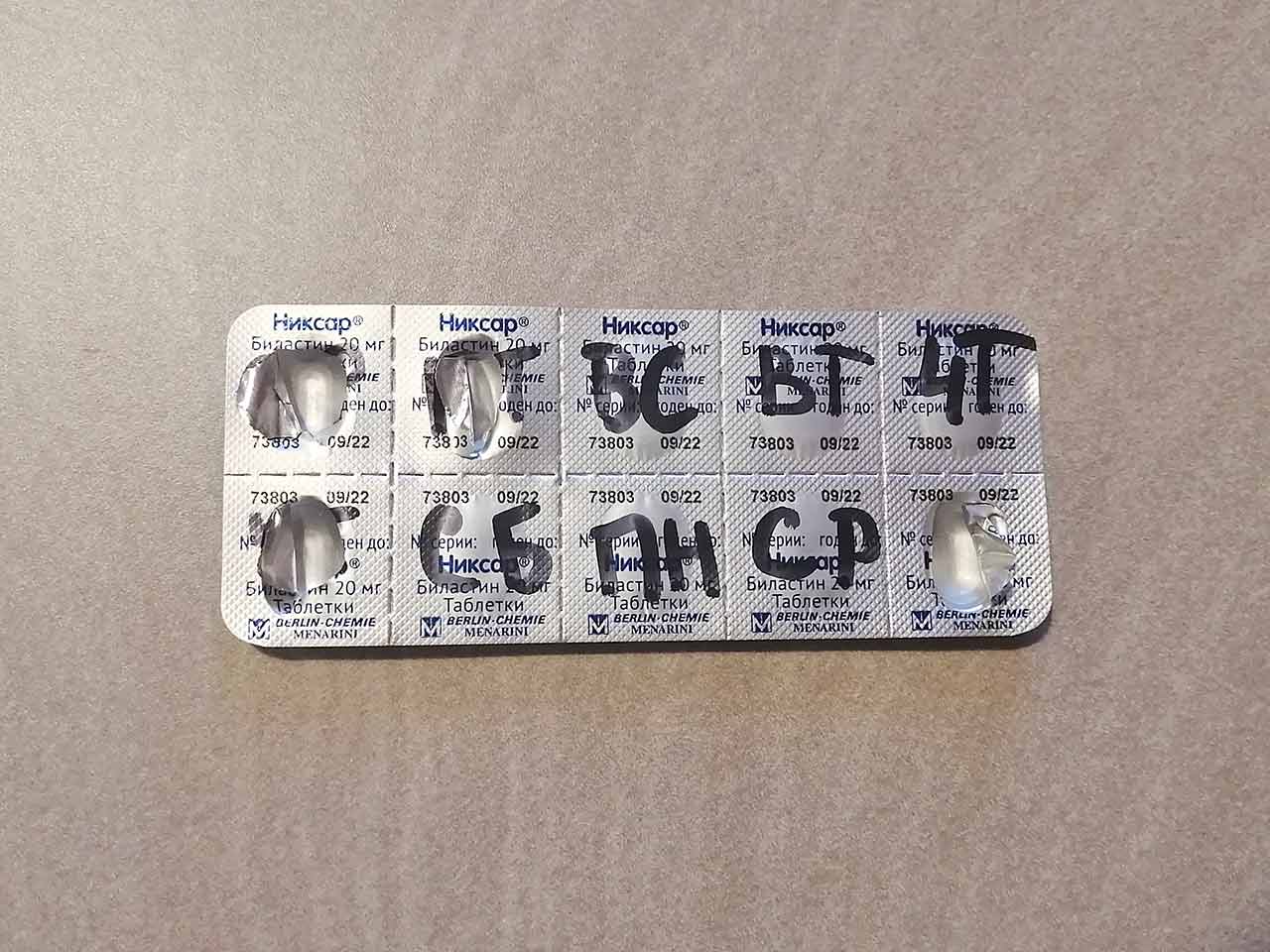
Любителям таких железобетонных решений напомню, что я
О ссылках на источники вдохновения
В выпуске подкаста Ильи Бирмана с Сергеем Стеблиной прозвучала мысль о том, что правильный способ критиковать
Как видите, я не последовал этому совету и честно сослался на источник вдохновения для этого поста. Обычно я всегда привожу такие ссылки. Не только потому, что так проще его написать.
Конечно, есть шанс, что автор неправильно понял «триггер», и его пост окажется «не в тему». И если не ссылаться на триггер, то вроде как и ошибки нет, просто обсуждается другая проблема. Но как раз честность проявляется еще и в том, что автор готов признать ошибку.
Давайте в оставшейся части я на примерах проиллюстрирую свою позицию.
Пример №1. Илья недавно выложил видео на 24 минуты с названием «0,(9) = 1. Как в это поверить?» В вводной части написано «Если вам никак не удается поверить, что 0,(9) = 1, то давайте я попробую убедить». Но масштаб проблемы при этом совсем неясен. Где все эти люди, которым не удается поверить, что 0,(9) = 1? Как они связаны с математикой? Почему важно их в этом убедить? Что будет, если их в этом не убеждать? В школьных и вузовских учебниках о совпадении формально разных десятичных дробей, одна из которых имеет период 9, написан от силы один абзац. Это всё при том, что сама запись рациональных чисел как бесконечных периодических десятичных дробей в науке не
Конечно, может быть такое, что к Илье постоянно приходят люди и говорят, что 0,(9) меньше 1. В этом случае идея записать видео и вместо ответа давать на него ссылку имеет право на жизнь. Но тогда бы я начал пост со слов «Мне раз в месяц пишут незнакомые люди о том, что…», и масштаб проблемы стал бы понятен.
Пример №2. У меня есть пост под названием «Какой мир видит фотон?», где я разбираю этот вопрос с точки зрения теории относительности. Для пояснения мотивации я честно добавил критикуемый ролик, в котором авторы попытались смоделировать, что бы засняла камера при движении через солнечную систему со скоростью света. А еще рассказал о семинарах по философии науки, на которых преподаватель утверждал, что из неспособности теории относительности описать движение одного фотона относительно другого следует, что ей на смену должна прийти
К научным теориям есть два главных требования. Первое — непротиворечивость — говорит о том, что любые способы рассуждения в рамках теории дают в каждой ситуации одинаковые предсказания. Второе — проверяемость в наблюдениях и опытах. Ни одно из этих требований не обязывает теорию относительности описать движение наблюдателя со световой скоростью, в то время как она утверждает, что это невозможно, и это утверждение не опровергнуто на практике.
С учетом описанных противоречий возникают вопросы и к преподавателю, и к самой философии науки как дисциплине. И когда я наткнулся на сайт преподавателя, я добавил ссылку и цитаты, чтобы показать источник этих вопросов. Одно дело, когда