интерфейсы

Самодельная типографская раскладка

В повседневном использовании мне не хватает двух символов на русской раскладке клавиатуры: решетки # и собаки @. Решетка обозначает заголовки в распространенной разметке markdown, а собака применяется в адресах электронной почты в чатах, чтобы «тегать» определенных людей (@supercoder) или всех подряд (@channel).

Для ввода решетки и собаки приходится постоянно переключаться с русского языка на английский и назад, да и сами эти символы вводить с шифтом. Ещё у Windows случается баг, когда она переключает язык не сразу, а после небольшой паузы: ты нажал Alt + Shift и уже что-то набираешь дальше, а язык не переключился. Приходится стирать, опять переключать язык на английский, выдерживать паузу, вводить символы, выдерживать паузу, переключаться на русский и опять выдерживать паузу перед продолжением набора.

Природу неудобства с этими специальными символами легко понять. Применять их в маркдауне и в чатах придумали в англоязычной среде с расчетом на англоязычную среду, когда никакой язык переключать не нужно. В других языках приходится терпеть.

Много лет назад я устанавливал типографскую раскладку Ильи Бирмана. Она специальным образом задействует правую клавишу Alt для ввода с клавиатуры расширенного набора символов. Например, вместо копирования откуда-то знака рубля ₽ можно просто нажать правый Alt + ^H_Р (то есть клавишу с русской буквой «эр»). Причем если установить раскладку и для русского языка, и для английского, то это сочетание клавиш будет работать и там и там.

Казалось бы, сам бог велел сделать в типографской раскладке не зависящие от языка комбинации клавиш Alt + 2 и Alt + 3 для ввода собаки и решетки. Тем более, так уже сделано и для знака доллара $ с комбинацией Alt + 4, и для квадратных скобок, которые тоже нужны в маркдауне. Но у Ильи в раскладке через Alt + 2 и Alt + 3 вводятся символы верхних индексов ² и ³. Сегодня такое решение кажется устаревшим. Я, кстати, вообще не помню, чтобы хоть раз в жизни использовал верхние индексы именно как эти отдельные символы, а не через инструменты форматирования.

Илья делал свою раскладку в программе MSKLC (Microsoft Keyboard Layout Creator). И нам никто не мешает создать собственную раскладку, отталкиваясь от своих потребностей. К счастью, MSKLC позволяет импортировать любую установленную раскладку и затем её отредактировать.

Я оставил большинство дополнительных символов как у Ильи. Единственные изменения — это прямой ввод символов `@# через комбинацию с правым Alt.

Стоит отметить, что программа MSKLC давно не обновлялась. Это заметно и по ее внешнему виду, и по требованию скачать древнюю версию .NET Framework 3.5 SP1 2008 года. К счастью, эти трудности не помешали создать свою версию раскладки.

Ещё одно интересное наблюдение заключается в том, что раньше типографская раскладка у меня не прижилась, потому что она ломает сочетание клавиш правый Alt + Enter для перехода в полноэкранный режим. Дискомфорт от сломанной привычки оказался сильнее пользы, которую приносила раскладка. Сейчас же я не испытываю особого дискомфорта. Похоже, изменения в интерфейсах и способах просмотра видео привели к тому, что жест правый Alt + Enter потерял своё значение.

Зарисовка для объяснения понятия формата

Нашел черновик статьи о понятии формата и вебе, которую я так и не написал и вместо которой снял видео из серии «в кресле препода». В черновик я успел написать только одну зарисовку для иллюстрации понятия формата. В видео зарисовка не вошла, вместо нее я сослался на известный ролик о работе техподдержки. Решил опубликовать черновик, может кому-нибудь пригодится.

---

Многие люди, даже профессионально занимающиеся разработкой сайтов, имеют смутные представления о понятии формата. Это понятие играет трудно уловимую, но важную роль в проектировании и разработке сайтов. Чем больше будущий сайт соответствует формату, тем быстрее пойдет разработка и тем проще будет посетителям.

Чтобы пояснить, что я подразумеваю под форматом, рассмотрим для примера газеты и книги. И то и другое — печатная продукция. На газетах распространяется небольшая порция ежедневной информации. Их после прочтения выбрасывают. Поэтому газеты печатают на дешевой тонкой бумаге. Книги объемнее, используются и хранятся долго. Их печатают на хорошей плотной бумаге и переплетают.

Можно представить, что будет с романом, напечатанным в формате газеты, а не формате книги. А вот более яркий пример. Представьте, что вы работаете в типографии и к вам приходит клиент.
— Я хочу напечатать свою поэму.
— Какой у вас тираж?
— Штук сто, где-то, буду раздавать друзьям и знакомым.
— Большая поэма? Сколько страниц?
— 100 страниц в Ворде. Но я не хочу, чтобы это была обычная книга. Я хочу напечатать на рулоне бумаги.
— Что? — вырывается у вас с плохо скрываемым удивлением.
— Ну на таком рулоне, типа как обои, только поменьше, — размахивает руками клиент.
— А чем вас книга не устраивает?
— Книга? Это вчерашний день. Рулон удобнее.
— Чем же он удобнее?
— Как чем? Страницы в книге нужно перелистывать. Это неудобно. На время перелистывания отрываешься от чтения. Ну и если книга закроется, трудно найти место, где читал, если не запомнить страницу.
— И что? А причем тут рулон?
— Ну как причем? Если напечатать на рулоне, то в процессе чтения его легко перематывать. Не нужно перескакивать с одной страницы на другую. И рулон можно спокойно отложить, он не закроется.
— Я вообще первый раз такое слышу. Все печатают и читают книги. Их удобно носить и держать на полке. И недостатки не такие уж и большие. Есть же закладки, оглавление. И перевернуть страницу ничего не стоит.
— Если все что-то делают, это не значит, что это правильно. Книги — вчерашний день. Я не хочу, чтобы читатель отрывался от моей поэмы, пока он перелистывает страницы.
— Извините, у нас нет такого оборудования, — мягко посылаете клиента.

Разговор в таком стиле вряд ли возможен о привычных предметах окружающего мира, но постоянно встречается при обсуждении компьютерных интерфейсов. Я задумался, почему так происходит, когда прочитал на хабрахабре статью о критике современных веб-технологий (HTML, CSS и JS) в сравнении с древним API для рисования окон. Хотя автор сравнивает инструменты для решения разных задач, и в комментариях разгорелась объемная дискуссия, статья набрала больше сотни плюсов. Я понял, что люди не имеют представления о формате. Это видно из вопроса автора:

Как нормально сверстать хотя бы такой блокнотик с закладками на CSS/HTML без извращений и большого количества JS кода вовсе не ради динамики, а прямо для самой отрисовки и позиционирования?

И из моего ответа:

Есть понятие формата, которое вы себе, судя по уже второму посту, плохо представляете. Нужно думать не о переносе конкретной реализации блокнотика из операционной системы в веб, а о решении той же задачи, которую решал блокнотик.

Очевидно, этот блокнотик был придуман, чтобы разместить в одном окне ограниченного размера как можно больше элементов управления. Даже если оставить в стороне уродливость внешнего вида, такое решение со вкладками не является очень хорошим примером интерфейса, так как пользователь не знает (или не помнит, ведь окном настройки не пользуются постоянно) плотность заполнения каждой вкладки и не имеет представления о том, сколько еще параметров можно изменить.

Проблема нехватки места в вебе прекрасно решается прокруткой. Поэтому, чтобы решить ту же задачу, нужно поместить друг под другом содержимое каждой вкладки, предваренное крупными заголовками. У такого метода целая куча достоинств. К прокрутке привыкли все. На больших экранах пользователь увидит сразу всю форму. Таким образом, на HTML/CSS блокнотика нет, но задача, которую он выполнял, решается.

При проектировании интерфейсов не нужно забывать о формате.

---

Еще в черновике было написано graceful degradation и progressive enhancement. Скорее всего, я хотел сказать, что начинать разработку надо с чистого HTML, а затем добавлять оформление в CSS и поведение в JS (progressive enhancement). А не делать наоборот — сначала разработать веб-приложение, а потом думать, как его заставить работать в простых браузерах. И хотел привести пример с веб-интерфейсом твитера. Лет 10 назад они переходили от клиентского рендеринга HTML к серверному, чтобы хоть что-то показывать в браузерах без JS и чтобы интерфейс не так тормозил.

Кстати, посмотрите само видео о понятии формата, если еще не посмотрели или уже забыли, о чем оно:

Визуальная конструкция элементов интерфейса

Нашел в некотором личном кабинете вот такой пример интерфейса. Я хочу остановиться на внешнем виде его элементов, и не буду сейчас подробно обсуждать проблему с теорией близости. Замечу лишь, что проблема не только в том, что переключатели находятся далеко от подписей. Кнопка «удалить аккаунт» из-за близости к подписи воспринимается как «удалить привязанный аккаунт Фейсбука», хотя на самом деле удаляет вообще всю учетную запись на этом сайте.

Можете ли вы понять по переключателям, включены ли они, или нет? Я воспринимаю этот элемент интерфейса как белый квадрат, перемещающийся внутри черного прямоугольника. Он находится справа, поэтому переключатель включен. Но я-то знаю, что соцсети у меня не подключены.

Выходит, что по задумке дизайнера черный прямоугольник перемещается без просвета внутри черной прямоугольной рамки. Хорошо, пробуем переключить:

Фирменный оранжевый цвет должен был показать активацию переключателя. Но у меня усилилось ощущение того, что белый квадрат, представляющий ручку переключателя, переместился налево. А оранжевый цвет говорит: «Внимание, выключено!».

Чтобы избавиться от неправильного восприятия элемента интерфейса, нужно изменить его конструкцию. Например, попробуем в отладчике скруглить уголки:

Получилось грубо, но состояние переключателей считывается однозначно. Полупрозрачный фон без рамки тоже хорошо работает:

Фирменный стиль не должен быть помехой для разработки и внедрения понятных элементов интерфейса.

Понятие формата в дизайне интерфейсов — В кресле препода №5

Когда-то давно хотел написать огромную статью о понятии формата в дизайне интерфейсов. Но так и не собрался, её всё равно никто не стал бы читать. А сейчас вспомнил об этом и записал видео.

Когда формулировал, почему моим словам стоит доверять, осознал, что у меня уже почти 13 лет опыта в коммерческой веб-разработке. Незаметно время летит :)

00:11 Почему моим словам стоит доверять: 13 лет опыта
00:42 Собирался рассказать о понятии формата давно
01:11 Для затравки: чем плохи выпадайки в вебе, пример личного кабинета интернет-банка
03:28 Понятие формата
04:56 Пример 1: формат веба и формат окон настройки старых операционных систем (сравнение из старой статьи на хабре)
08:03 Комментарий к статье, обращающийся к понятию формата
10:42 OS/2 умер
12:09 Окно настройки — почему такое? Ограничение 1: физический размер экранов
14:24 Ограничение 2: размер видеопамяти
15:26 Ограничение 3: частота обновления
18:53 Ограничение 4: работа без драйверов
19:54 640*480 — естественное ограничение в конце 90-х
20:58 Особенности формата веба
22:47 Сравнивать надо функциональность
25:28 Бессмысленность претензий к вебу
26:52 Эволюция интерфейса настройки Windows
32:28 Пример 2: Одностраничные приложения
33:54 Админка моего движка как пример одностраничного приложения
37:25 Как бы сейчас спроектировал интерфейс админки
41:42 Обсуждаем извлеченные уроки и дизайн выпадайки из личного кабинета интернет-банка
46:17 Итог

Стили для печати и конвертация в PDF

Постоянные читатели помнят, что у меня есть двухпанельный редактор математических текстов Upmath: слева пишете текст с разметкой на маркдауне и латехе, справа получаете результат.

От пользователя пришло письмо, в котором он спрашивает, есть ли конвертация маркдауна и латеха в PDF. Вопрос задают не первый раз. Мне сообщали о каких-то утилитах вроде pandoc. Я отвечал, что программировать это не буду.

Главная задача сервиса Upmath — подготовка математических текстов для публикации в вебе. Результат его работы — html-код. Если кому-нибудь нужен PDF, его можно получить с помощью самого латеха. На выходе будет превосходно сверстанный документ со всеми типографскими плюшками.

Но сейчас я задумался. Не всем нужен высококачественный PDF. Кто-то готовит текст самостоятельной работы для учеников и студентов. Кто-то распечатывает черновики, чтобы править ошибки. Что мешает получить PDF прямо сейчас?

Печатать можно напрямую из браузера. Хоть на настоящем принтере, хоть в pdf-документ. Я до сих пор не задумывался об этом, и не подготовил стили для печати (раньше вообще svg-картинки нормально не печатались). Получалась бесполезная страница с началом текста и его исходником:

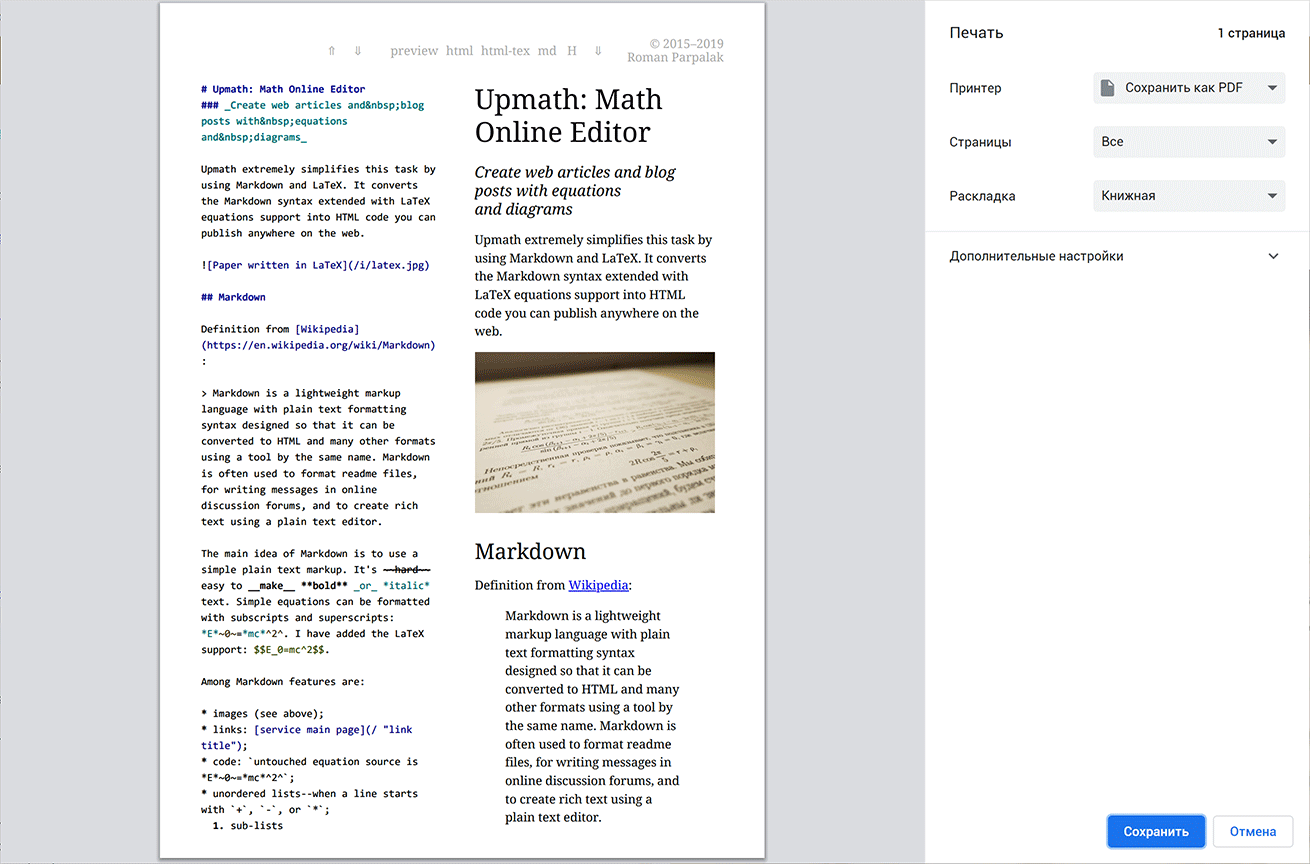
Мне ничего не стоило добавить стили для печати. Результат сразу преобразился:

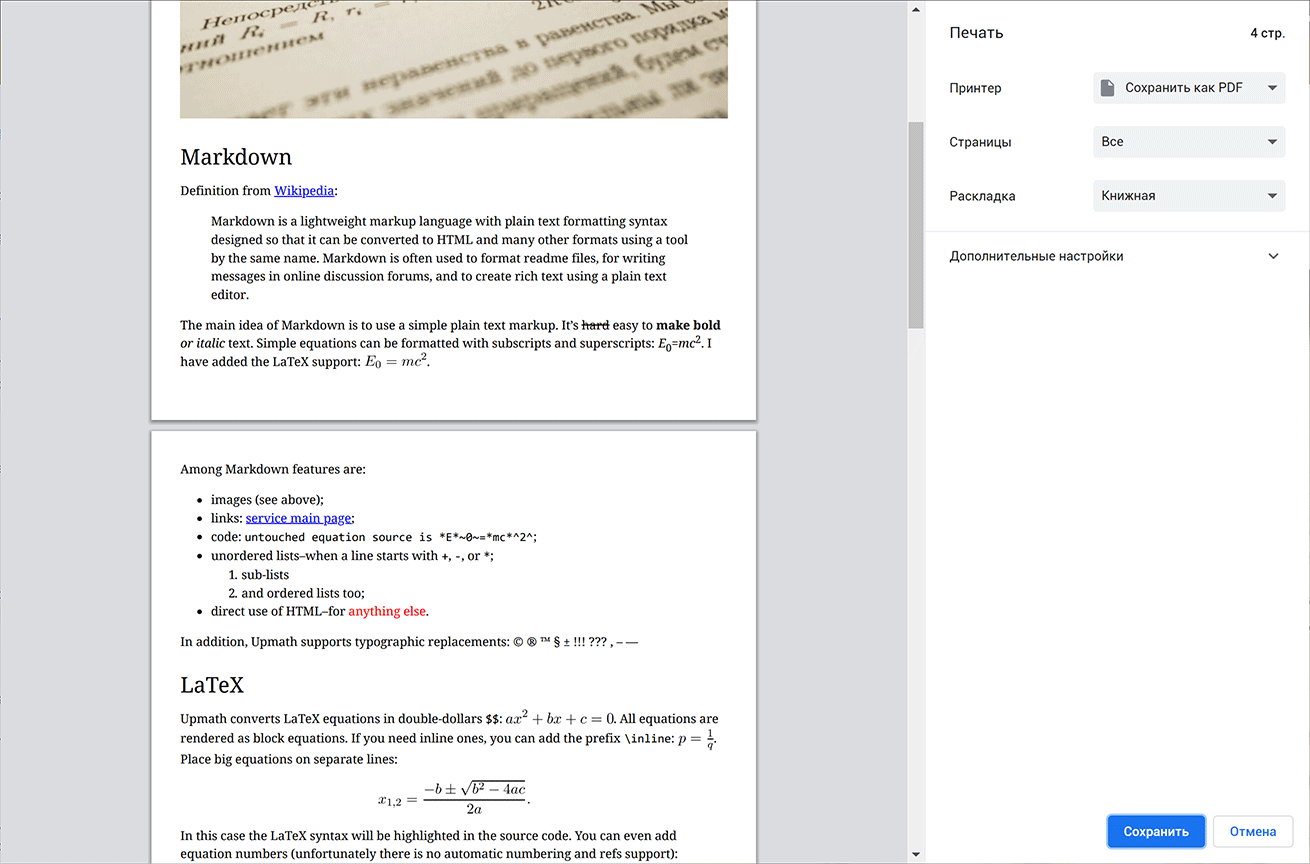
Качество получающихся документов мне не очень нравится. Я добился того, чтобы картинки не разбивались на две страницы. Но исключить разрыв страницы после заголовков у меня не получилось. Не понимаю, почему ни хром, ни FF не понимают инструкцию

h1, h2, h3 {
    break-after: avoid;
}

Будем ждать, пока эти баги в браузерах будут исправлены.

Отменная кнопка

Синхронная прокрутка

Этот текст я написал в том числе и для себя, чтобы в следующий раз не попадать в ловушку «почему два года назад я сделал так криво, сейчас всё исправлю».

Иногда в интерфейсе нужно одновременно показать два документа с синхронной прокруткой. Прокручиваешь левый документ, и правый тоже прокручивается до соответствующего места. И наоборот. Может показаться, что задача синхронной прокрутки не слишком сложная. Но на самом деле это не так.

Пример синхронной прокрутки есть в каждом интерфейсе просмотра изменений файлов. Вот PhpStorm:

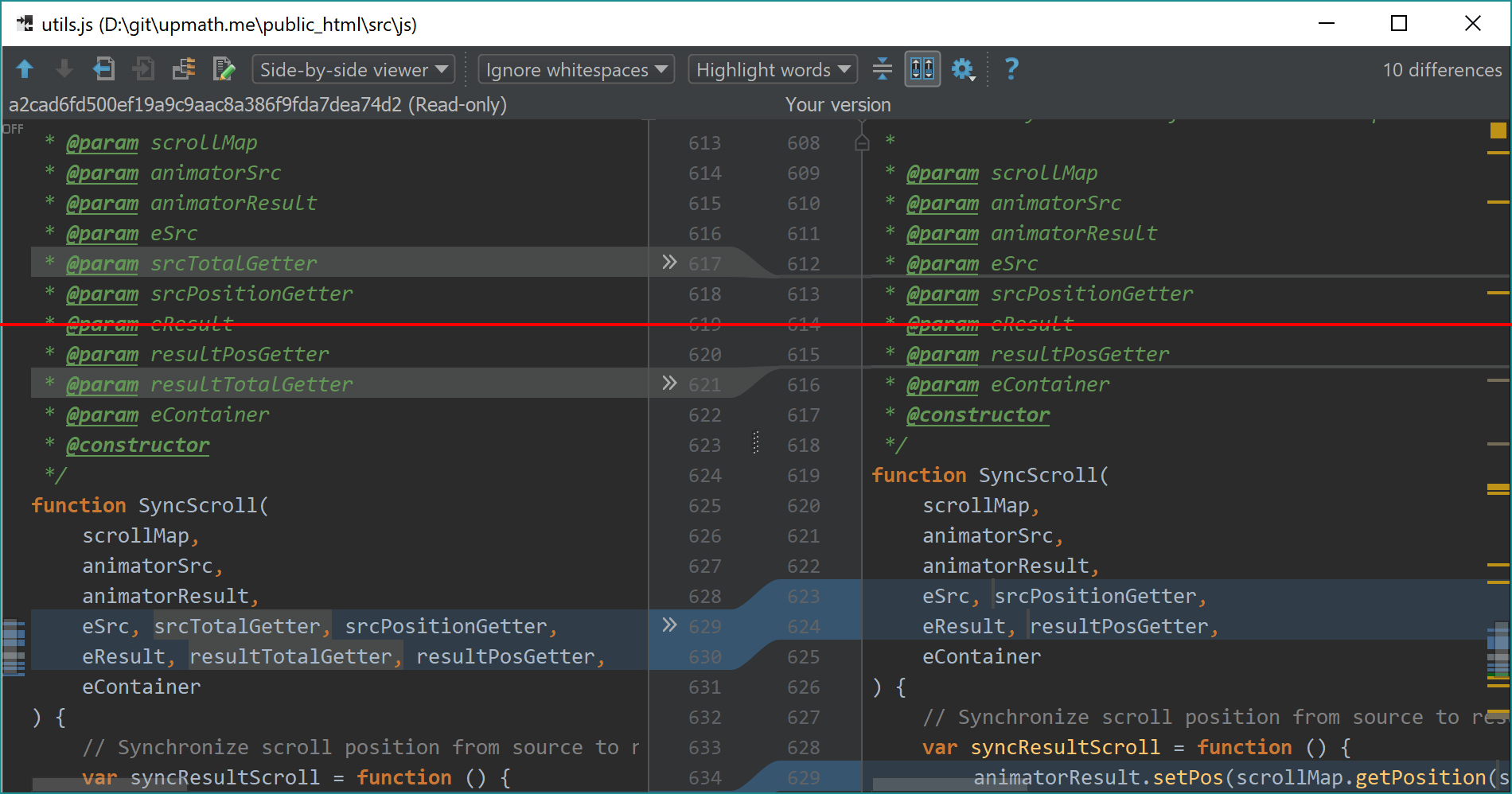
При прокрутке одной версии документа вторая всегда выравнивается так, чтобы на красной линии оказались соответствующие строки. Аналогичный способ я выбрал для своего редактора математических текстов, только ориентир выравнивания сделал посередине:

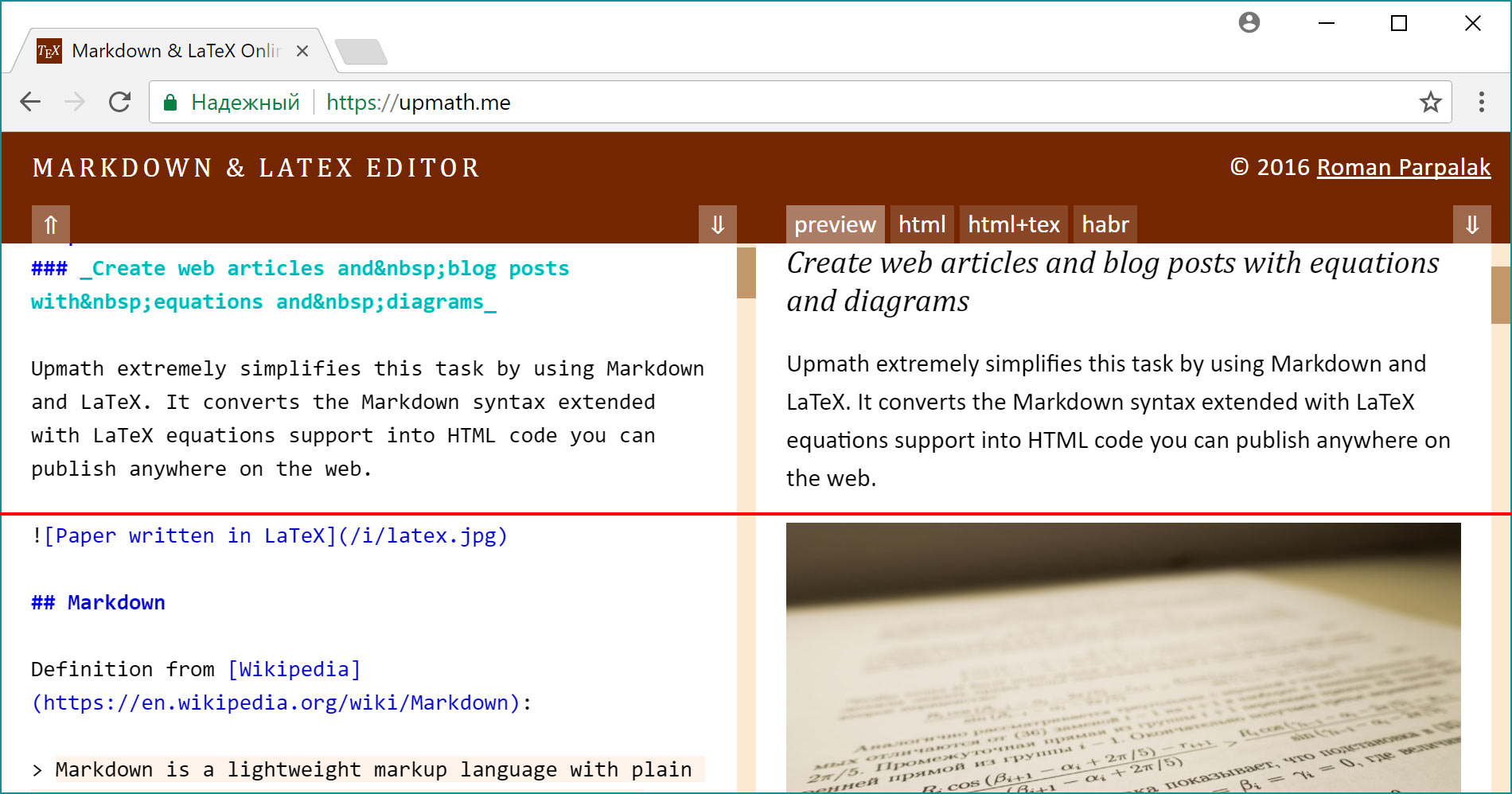
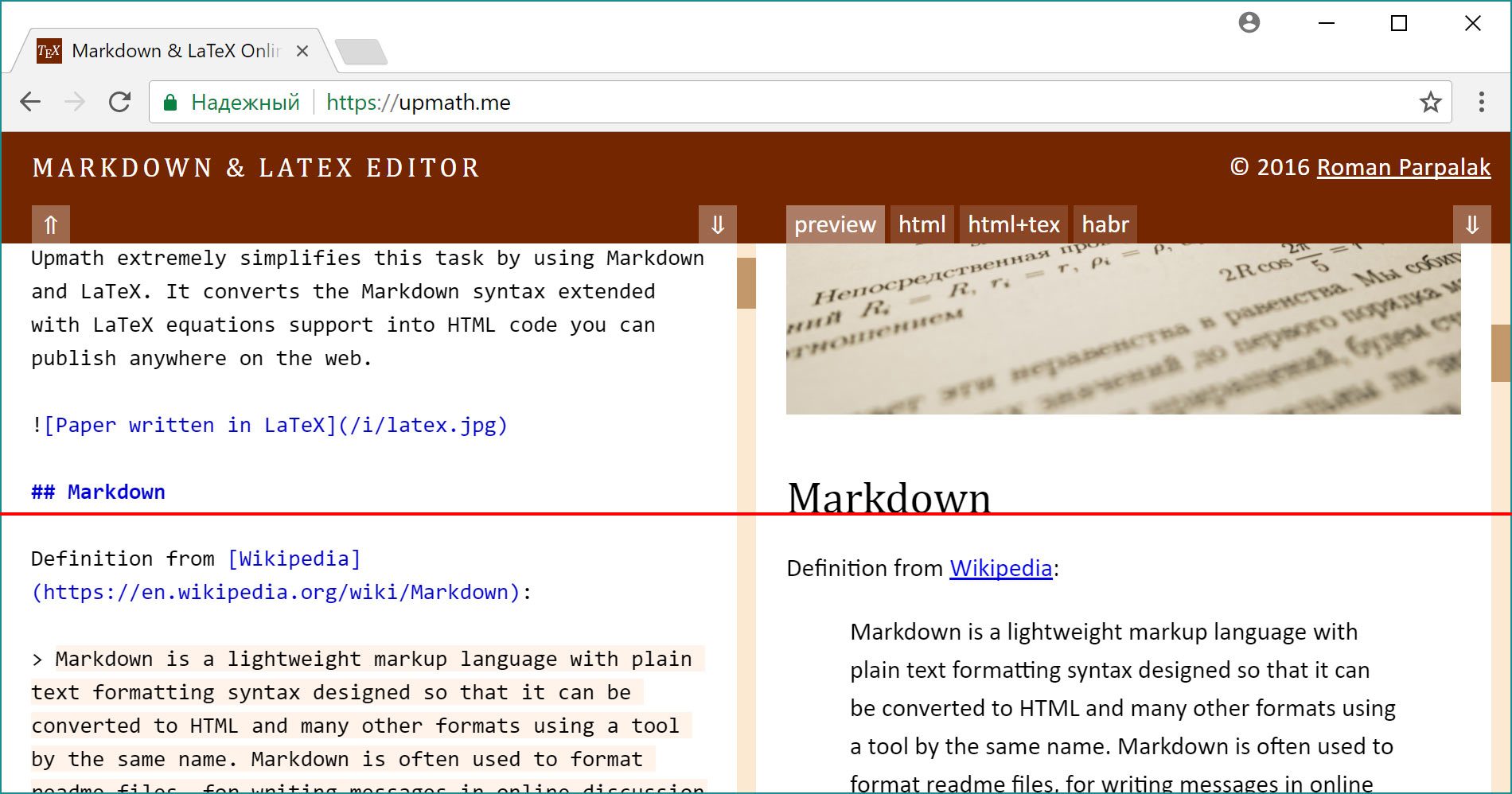
Здесь мы набираем исходный код и сразу же видим результат. Обратите внимание на неравномерность прокрутки. Слева картинка кодируется одной строкой, а справа она занимает почти всю высоту прокручиваемой области.

Такая неравномерность приводит к ряду проблем. Когда картинка добавляется последней строчкой, в предпросмотре отображается только ее верхушка:

Это естественное поведение алгоритма с выравниванием по ориентиру в центре. И его хотелось бы улучшить. Но от линии-ориентира отказаться нельзя. Например, если первый документ прокручен на 90%, то мы не можем просто так прокрутить второй документ тоже на 90%. Из-за неравномерности распределения элементов в видимую область могут попасть совершенно разные абзацы.

Другая идея — сделать ориентир не фиксированным, а подвижным. Сначала ориентир расположен вверху. Затем, по мере прокрутки, он сдвигается вниз. Но и здесь нас ждут скользкие моменты. Например, мы знаем, что начало одного и того же абзаца находится в левом документе на высоте в 30%, а в правом на 50%. Пусть левый документ прокрутили на 30%. Тогда мы говорим, что ориентир тоже находится на 30% высоты экрана, переводим 30% в 50%, и располагаем правый документ так, чтобы абзац был на 30% высоты экрана. Проблема в том, что обратное преобразование не обязано давать тот же самый результат. Действительно, тот же самый абзац будет использоваться при прокрутке правого документа на 50%, и в общем случае это разные положения прокрутки. В такой реализации встречаются странные скачки прокрутки при переключении фокуса между документами и даже немонотонность зависимой прокрутки: если вы прокручиваете один документ вниз, то другой в некоторые моменты будет двигаться не вниз, а вверх.

У меня была мысль отказаться от двух прокручиваемых областей, прокручивать только исходный код и умным алгоритмом выводить в области предпросмотра соответствующую область документа. Но проблемы синхронной прокрутки, о которых я рассказал, мешают это сделать.

Похоже, полностью избавиться от проблем синхронной прокрутки вообще нельзя. Вернемся к сравнению файлов. Предположим, в одном файле 100 строк, во втором я превратил сотую строку в еще 400. Прокручивая первый файл, мы никогда не увидим новые 400 строк второго. Как бы мы ни выравнивали второй файл, все 400 строк на экран не поместятся. Это значит, что нельзя убирать вторую прокрутку.

В своем редакторе я оставил синхронизацию прокрутки по ориентиру, но дополнил ее условием: если один документ полностью прокручен вверх или вниз, то второй документ прокручивается полностью.

О режимах редактора vim

На хабре идут обсуждения вима: «Режимы не фатальный недостаток, а киллер-фича» и «Киллер-фича в vim — это режимы? Серьёзно?».

И даже в комментариях никто не вспомнил старика Раскина. Именно он писал в книге «Интерфейс» о проблемах модальности и режимов (конспект нескольких глав книги тоже есть на хабре). Причем и в статьях, и у Раскина совпадает не только используемое понятие, но и его название — «режим».

Чтобы выжить, когда случайно оказываешься в виме, я помню две вещи. Если редактор не печатает, будто сломалась клавиатура, нужно нажать i. Чтобы выйти, нужно нажать эскейп-двоеточие-q. Или wq, если нужно сохранить изменения.

Интерфейсные решения вима устарели чуть менее, чем перфокарты. Сравнивать вим и современные IDE — всё равно что сравнивать интерфейс Нокии 3310 и любого современного смартфона.

В этой заметке я почти удержался от использования фразы «дерьмо мамонта».

Естественная анимация в интерфейсах

Анимация в интерфейсе делает наглядным изменение его состояния. Например, при неудачной отправке длинная форма прокручивается к неправильно заполненному полю. Или увеличивающаяся по нажатию фотография раздвигает окружающие элементы.

Без анимации сложнее воспринимать резкие и внезапные изменения. Вместе с тем анимация должна быть короткой и ненавязчивой, чтобы не мешать пользователю.

Анимация кажется естественной, когда повторяет привычное движение предметов окружающего мира. Я расскажу, как делал анимацию в своем редакторе математических текстов Upmath на основе физических законов. Готовый результат в изолированном окружении смотрите на демо-странице, где один блок следует за другим при движении мыши.

Вспоминаем физику

Перемещение объектов описывается изменением координат x с течением времени t. Если вы попытаетесь подобрать функцию x(t) «на глазок», потратите много времени, добиваясь плавного и естественного движения. Что выбрать? Гиперболу? Параболу? Куда ее переместить? Как повернуть?

За примерами движения лучше всего обратиться к предметам окружающего мира. Математический закон их движения диктуется физикой. Толкнем брусок, лежащий на столе. Он проходит определенное расстояние, замедляясь под действием силы трения. В хорошем приближении сила сухого трения скольжения постоянна, и зависимость x(t) оказывается параболой. Такое замедление можно использовать, если в начальный момент объект анимации уже двигался.

$$\begin{tikzpicture} \def\t{0} \def\r{3.4} \begin{axis}[width=10cm,height=7cm, ticks=none, xmin=-0, xmax=3.8, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true,mark size=1 ] \addplot[smooth,blue,domain=\t:\r,samples=80]{-(x-\r)^2} node[pos=0.75,black,anchor=south east,inner sep=2pt]{$x=A+Bt+Ct^2$}; \addplot[dashed,domain=\r-0.7:\r,samples=2]{0}; \addplot[mark=*] coordinates {(\t,-\r*\r)}; \addplot[mark=*,green!50!black] coordinates {(\r,0)} node[pin=-90:{\footnotesize{\text{\sffamily плавная остановка :)}}}]{}; \end{axis} \end{tikzpicture}$$

Рис. 1. Торможение сухим трением по параболе

Сила вязкого трения пропорциональна скорости движения тела. В таком случае тело будет двигаться к точке остановки по экспоненте за бесконечно большое время. Если экспоненту исказить, чтобы ограничить время движения, такая анимация будет казаться неестественной. Из-за трудностей с остановкой в разумное время не следует использовать модель вязкого трения, только если симуляция самого вязкого трения не является целью.

$$\begin{tikzpicture} \def\t{0} \def\r{3.8} \begin{axis}[width=10cm,height=7cm, ticks=none, xmin=-0, xmax=3.8, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true,mark size=1 ] \addplot[smooth,blue,domain=\t:\r,samples=80] {1-exp(-x*1.0)} node[pos=0.45,black,anchor=south east,inner sep=2pt]{$x=A-Be^{-\alpha t}$}; \addplot[dashed,domain=\t:\r,samples=2]{1}; \addplot[mark=*] coordinates {(\t,0)}; \addplot[red!80!black] coordinates {(3.4,1)} node[pin=-90:{\footnotesize{\text{\sffamily не останавливается :(}}}]{} ; \end{axis} \end{tikzpicture}$$

Рис. 2. Торможение по экспоненте в вязкой среде

Отклоненный от положения равновесия маятник (или грузик на пружине) плавно набирает скорость, проходит положение равновесия и плавно тормозит. Затем движение повторяется в обратную сторону, и так до бесконечности (если трения нет). График такого движения — синусоида. Периодический повтор нам не особо интересен, а вот движение маятника между крайними точками получается плавным и естественным.

$$\begin{tikzpicture} \def\t{0} \def\r{3.1415} \begin{axis}[width=10cm,height=7cm, ticks=none,mark size=1, xmin=-0.5, xmax=3.6, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true ] \addplot[smooth,blue,domain=\t:\r,samples=80] {1-cos(deg(x))} node[pos=0.52,black,anchor=south east,inner sep=2pt]{$x=A-B\cos\omega t$}; \addplot[dashed,domain=\t:\t+0.6,samples=2] {1-cos(deg(\t))}; \addplot[dashed,domain=\r-0.6:\r,samples=2] {1-cos(deg(\r))}; \addplot[mark=*,green!50!black] coordinates {(\t,0)} node[pin=90:{\footnotesize{\text{\sffamily плавный запуск :)}}}]{}; \addplot[mark=*,green!50!black] coordinates {(\r,2)} node[pin=-90:{\footnotesize{\text{\sffamily\quad плавная остановка :)}}}]{}; \end{axis} \end{tikzpicture}$$

Рис. 3. Движение маятника по синусоиде между крайними точками

В JS-библиотеках и CSS есть заготовки easing-функций для создания специальных эффектов. Почти все заготовки следует использовать с осторожностью, тщательно проверяя их уместность. Только синусоида более-менее универсальна:

• Синусоидальная траектория переводит тело из одного покоящегося положения в другое.
• Продолжительность такого движения ограничена по времени и равна половине периода. То есть эта продолжительность зависит не от внешних обстоятельств и начальных условий, а только от свойств самой системы, и определяется соотношением жесткости и инерционности.

Обычно я выбираю длительность анимации по синусоиде в 200 миллисекунд. Такая длительность в несколько раз больше времени реакции человека. Анимация хорошо заметна, но не успевает раздражать.

Давайте научимся проводить синусоидальную траекторию по начальным условиям, времени движения и точке остановки.

Как провести синусоиду через две точки

Пусть тело покоится в начальный и конечный момент времени. Тогда касательные к графику в точках t₁ и t₂ горизонтальны, а сам график — это полупериод синусоиды.

$$\begin{tikzpicture} \def\t{0} \def\r{3.1415} \begin{axis}[ ticks=none, xmin=-1, xmax=4.5, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true ] \addplot[smooth,blue,domain=\t:\r,samples=80] {1-cos(deg(x))}; \addplot[dashed,domain=\t:\t+1,samples=2] {1-cos(deg(\t))}; \addplot[dashed,domain=\r-1:\r,samples=2] {1-cos(deg(\r))}; \addplot[mark=*,mark size=1] coordinates {(\t,0)} node[pin=95:{$(t_1,x_1)$}]{} ; \addplot[mark=*,mark size=1] coordinates {(\r,2)} node[pin=-85:{$(t_2,x_2)$}]{} ; \end{axis} \end{tikzpicture}$$

Рис. 4. График движения между двумя положениями покоя

Уравнение, описывающее полупериод синусоиды, легко подобрать:

$$x(t)=x_1+{x_2-x_1\over 2}\left[1 - \cos\left(\pi{t-t_1\over t_2-t_1}\right)\right].$$

После окончания одной анимации мы можем начинать другую опять по этой формуле. Но что делать, если новая анимация должна начаться, пока еще не закончилась старая? Чтобы обеспечить плавность движения, мы останавливаем текущую анимацию (синяя линия) и начинаем новую анимацию (красная линия) с ненулевой начальной скоростью:

$$\begin{tikzpicture} \def\tgnt{0.7} \def\t{0} \def\r{3.1415} \def\tb{1} \def\rb{\r+\tb} \def\dx{1.27} \begin{axis}[ ticks=none, xmin=-1, xmax=4.9, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true,mark size=1 ] \addplot[smooth,blue,domain=\t:\tb,samples=80] {-cos(deg(x))+1}; \addplot[smooth,dotted,blue,domain=\tb:\r,samples=10] {-cos(deg(x))+1}; \addplot[blue,dashed, domain=\t:\t+\tgnt,samples=2] {-cos(deg(\t))+1}; \addplot[smooth,thick,red,domain=\tb:\rb,samples=80] {-1.5*cos(deg(1+0.69*(x-\tb)))+\dx}; \addplot[dashed,red,domain=\tb-\tgnt:\tb+\tgnt,samples=2] {-1.5*cos(deg(\tb))+\dx+sin(deg(\tb))*(x-\tb)}; \addplot[dashed,red,domain=\rb-\tgnt:\rb,samples=2] {1.5+\dx}; \addplot[mark=*] coordinates {(\t,0)}; \addplot[mark=*] coordinates {(\tb,1-cos(deg(\tb)))} node[pin=-85:{$(t_1,x_1)$}]{} ; \addplot[mark=*] coordinates {(\r,2)}; \addplot[mark=*] coordinates {(\rb,1.5+\dx)} node[pin=-85:{$(t_2,x_2)$}]{} ; \end{axis} \end{tikzpicture}$$

Рис. 5. График движения с ненулевой начальной скоростью

Без математических вычислений не получится написать формулу, соответствующую красной линии. Давайте проделаем эти вычисления.

Семейство всех возможных синусоид описывается уравнением

$$f(t)=A\cos\omega (t-t_2)+B\sin\omega (t-t_2)+C$$(1)

с четырьмя неизвестными параметрами A, B, C и $$\omega>0$$. Я сдвинул начало отчета времени в точку t₂, чтобы сразу избавиться от второго слагаемого. Действительно, производная $$f'(t_2)=B\omega$$ должна быть нулевой, потому что касательная в точке t₂ горизонтальна. Это возможно, когда B=0.

Так как $$f(t_2)=x_2$$, то подставляя $$t=t_2$$ в (1), получаем $$f(t_2)=A+C$$. Отсюда исключаем C:

$$f(t)=x_2 + A\left[\cos\omega (t-t_2)-1\right].$$

Продифференцируем, чтобы найти скорость

$$f'(t)=-A\,\omega\sin\omega (t-t_2).$$

Нам известно положение x₁ и скорость v в начальный момент времени:

$$\begin{cases} x_1\!\!\!\!\!&=x_2+A\left[\cos\omega(t_1-t_2)-1\right],\\ v\!\!\!\!\!&=-A\,\omega\sin\omega(t_1-t_2). \end{cases}$$

Из этой системы уравнений нужно найти A и $$\omega$$. Пора вводить новую переменную $$k=\omega(t_2-t_1)$$ вместо $$\omega$$. Ее смысл — разность фаз синусоиды в начальной и конечной точке. Например, для графика на рис. 4 $$k=\pi$$, потому что на промежутке $$(t_1,t_2)$$ укладывается полупериод синусоиды. На рис. 5 $$k<\pi$$, потому что $$t_2-t_1$$ меньше половины периода.

После подстановки и небольших преобразований приходим к системе

$$\begin{cases} x_2-x_1&=A\left(1-\cos k\right),\\ v(t_2-t_1)\!\!\!\!&=A\,k\sin k. \end{cases}$$

Разделим почленно первое уравнение на второе:

$${x_2-x_1\over v(t_2-t_1)}={1-\cos k\over k\sin k}\quad \Rightarrow\quad{1-\cos k\over\sin k}=\alpha k,\quad\text{где} \ \alpha={x_2-x_1\over v(t_2-t_1)}.$$

Параметр $$\alpha$$ в правой части известен заранее. Он определяет требуемый характер движения. Если $$\alpha\gg1$$, то начальная скорость мала, тело сначала должно ускориться. Если $$\alpha\ll1$$, начальная скорость велика, тело должно замедляться.

Тригонометрические функции в левой части сводятся к тангенсу половинного угла. В итоге у нас нелинейное уравнение относительно k:

$$\text{tg}\,{k\over2}=\alpha k.$$(2)

Проанализировать его решения можно на графике. Нарисуем график левой и правой части при некоторых значениях параметра $$\alpha$$:

$$\begin{tikzpicture}\small \def\aa{1.5} \def\ab{0.3} \def\ac{-0.5} \begin{axis}[legend pos=south east,mark size=1,samples=2, restrict y to domain=-8:8, width=12cm, height=250pt, xmin=-10.5, xmax=10.5, ytick={-6,-3,...,6}, xtick={-9.4247,-3.1416,...,10}, xticklabels={$-{3\pi}$,$-{\pi}$,${\pi}$,${3\pi}$}, axis x line=center, axis y line=center, xlabel=$k$] \addplot[blue!70!black,domain=-9.4247:9.4247,semithick,samples=802]{tan(deg(x/2))}; \addplot[red]{\aa*x}; \addplot[green!70!black,domain=-9.4247:9.4247]{\ab*x}; \addplot[olive,domain=-9.4247:9.4247]{\ac*x}; \addplot[mark=*] coordinates {(2.65,3.97)} node[anchor=west,inner sep=2pt]{$A$}; \addplot[mark=*] coordinates {(8.69,2.61)} node[anchor=west,inner sep=1pt,yshift=-4pt]{$B$}; \addplot[mark=*] coordinates {(4.06,-2.03)} node[anchor=west,yshift=2]{$C$}; \legend{$y=\tg k/2$,$y=\aa\,k$,$y=\ab\,k$,$y=\ac\,k$} \end{axis} \end{tikzpicture}$$

Рис. 6. Графическое решение уравнения (2)

Обсудим получившиеся решения.

1. Рассмотрим точку A. Это решение существует при $$\alpha>1/2$$ и соответствует изображенному на рисунке 5: $$\begin{tikzpicture} \def\t{1} \def\r{3.1415} \begin{axis}[width=1.9cm,height=2cm,hide axis,ticks=none, xmin=\t,xmax=\r,mark size=0.3] \addplot[smooth,blue,domain=\t:\r,samples=80] {-cos(deg(x))}; \addplot[mark=*] coordinates {(\t,-cos(deg(x)))}; \addplot[mark=*] coordinates {(\r,-cos(deg(x)))}; \end{axis} \end{tikzpicture}$$. Как ожидалось, $$k<\pi$$. В пределе нулевой скорости $$\alpha\to\infty$$, красная прямая совпадет с осью ординат, точка A уйдет по тангенсоиде в бесконечность. В этом пределе $$k\to\pi$$. Пока всё идет правильно.

2. Точка C отвечает значению $$\alpha<0$$. Такое случается, когда тело в первый момент времени движется вперед, а надо двигаться назад. Теперь $$\pi<k<2\pi$$. Движение описывается фрагментом синусоиды, большим чем полупериод, но меньшим, чем период: $$\begin{tikzpicture} \def\t{-1.7} \def\r{3.1415} \begin{axis}[width=2.2cm,height=2cm,hide axis,ticks=none, xmin=\t,xmax=\r,mark size=0.3] \addplot[smooth,blue,domain=\t:\r,samples=80] {cos(deg(x))}; \addplot[mark=*] coordinates {(\t,cos(deg(x)))}; \addplot[mark=*] coordinates {(\r,cos(deg(x)))}; \end{axis} \end{tikzpicture}$$. Тело тормозит, останавливается, движется назад и останавливается в требуемом месте.

3. Из графика видно, что при $$0<\alpha<1/2$$ точка B попадает в диапазон $$2\pi<k<3\pi$$. Тело пройдет по синусоиде больше, чем полный период колебаний: $$\begin{tikzpicture} \def\t{-1.6} \def\r{2*3.1415} \begin{axis}[width=2.5cm,height=2cm,hide axis,ticks=none, xmin=\t,xmax=\r,mark size=0.3] \addplot[smooth,blue,domain=\t:\r,samples=80] {cos(deg(x))}; \addplot[mark=*] coordinates {(\t,cos(deg(x)))}; \addplot[mark=*] coordinates {(\r,cos(deg(x)))}; \end{axis} \end{tikzpicture}$$. Причина такого странного решения в том, что точка остановки находится слишком близко по сравнению с характерным расстоянием v (t₂ − t₁). Поэтому провести синусоиду без дополнительной остановки и возврата не получится.

Небольшое лирическое отступление: похожие на (2) уравнения возникают при решении задач квантовой механики про уровни энергии частиц в прямоугольных потенциальных ямах. Там приходится сшивать, например, синусоиду и экспоненту. Условие отсутствия изломов дает подобные уравнения с бесконечным количеством корней.

Приближенное решение

Мы решили математическую задачу проведения синусоиды, но жизнь от этого проще не стала. Во-первых, чтобы определить параметры синусоиды, надо решить нелинейное уравнение (2). Привет, итерационные методы! Во-вторых, уравнение имеет бесконечное количество решений, а требуемое решение не всегда существует.

Эти трудности возникли от того, что мы зафиксировали продолжительность анимации ровно в 200 миллисекунд. Однако ничего страшного не случится, если анимация продлится, скажем, 180 миллисекунд. Или даже 250 миллисекунд. Нам важнее остановка в заданном месте, а точной продолжительностью анимации мы пожертвуем для упрощения расчетов.

Ослабив требования на продолжительность анимации, мы проделаем такой трюк. Предположим, что у нас есть приближенное решение $$k'$$ нелинейного уравнения (2). Оно является точным решением уравнения с другим параметром

$$\alpha'={1\over k'}\,\text{tg}{k'\over 2},$$

Ему соответствует другое время окончания анимации:

$$t_2'=t_1+{x_2-x_1\over v\alpha'}.$$

Теперь неизвестные параметры траектории A и $$\omega$$ элементарно выражаются через $$k'$$ и $$\alpha'$$.

Я подобрал подходящее для наших целей приближение к уравнению (2):

$${1\over 2\alpha}\approx1-\left({k\over\pi}\right)^2.$$

Синяя сплошная линия соответствует точному уравнению (2), а красная пунктирная — его приближению:

$$\begin{tikzpicture}\small \begin{axis}[legend pos=south east, restrict y to domain=-8:8, width=12cm, xmin=-7.3, xmax=7.3, ytick={-6,-3,...,6}, xtick={-6.2832,-3.1416,...,10}, xticklabels={$-{2\pi}$,$-{\pi}$,$0$,${\pi}$,${2\pi}$}, axis x line=center,axis y line=center, xlabel=$k$,ylabel=$\alpha$] \addplot[smooth,samples=580,blue!70!black,domain=-7:7]{tan(deg(x/2))/x}; \addplot[smooth,samples=580,red,dashed,domain=-7:7]{0.5/(1 - (x/pi)^2)}; \legend{$(1/k)\,\text{tg}\,k/2$,$0.5/\!\left[1 - ({k/\pi})^2\right]$} \end{axis} \end{tikzpicture}$$

Рис. 7. Сравнение точного соотношения (2) и его приближения

А еще в случае $$0<\alpha<1/2$$ предлагаю взять $$\alpha'$$ чуть больше, чем 1/2, и сократить время анимации, чтобы избежать отскока и возврата.

Применение

Код и пример использования есть на демо-странице. Поводите мышью и посмотрите, как черный блок следует за оранжевым.

Описанную схему я разработал для синхронной прокрутки исходного кода и предпросмотра в своем редакторе математических текстов Upmath.

Идею и первоначальную реализацию нашел на демо-странице js-парсера markdown-it. В их варианте анимация получилась рваной и подтормаживающей. Тому есть несколько причин:

1. Для анимации применяется линейная функция: $(...).stop(true).animate( {scrollTop: ...}, 100, 'linear' ). Вместо гладкого графика получается ломаная.
2. Анимация через jQuery().stop().animate() тормозит по сравнению с requestAnimationFrame().
3. Чтобы избежать падения производительности, «проглатываются» события onscroll, следующие чаще чем 50 миллисекунд. В моем варианте такой проблемы нет. Последовательные события onscroll корректируют положение точки остановки и не замедляют анимацию.

Чтобы добиться важной для продукта качественной анимации, я проработал метод вычисления на основе физических уравнений, и реализовал его через специальный браузерный метод requestAnimationFrame(). Метод хорошо работает при любой прокрутке: клавишами PageUp/PageDown, через перемещение полос прокрутки, колесико мыши, тачпад, тачскрин.

Статья впервые опубликована на хабре.

Последовательная загрузка торрентов ★

Самая важная функция торрентов, помимо собственно файлообмена, — это последовательное скачивание файлов.

В процессе обмена торрент-клиент сам выбирает фрагменты файлов для приема и передачи, обычно исходя из информации об их доступности. На практике это приводит к загрузке фрагментов в случайном порядке.

Порядок загрузки не имеет значения, если вы скачиваете фильм на медленном соединении. Или программу. Или образ диска операционной системы. Но если у вас быстрый интернет, и двухчасовой фильм скачается за час, не получится ли загружать фрагменты фильма последовательно и сразу отправлять их в плеер? Тогда начинать просмотр можно сразу, не дожидаясь полной загрузки файла.

Пионер технологии uTorrent

Впервые подобная функция под названием streaming появилась в uTorrent версии 3.0. Он скачивал подряд несколько первых фрагментов и умел отдавать их через встроенный сервер потокового видео. Просматривать это потоковое видео можно было через плеер VLC. По мере просмотра зона последовательной предзагрузки продвигалась вперед, чтобы обеспечить систему достаточным для воспроизведения набором данных.

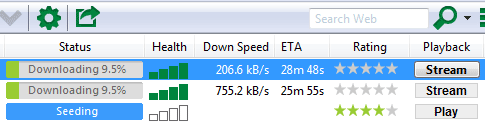
Интуиция подсказывает, что сложная схема с участием торрентокачалки, встроенного в нее сервера потокового видео и плеера VLC может заработать не так, как ожидается. И практика эти опасения подтверждает.

Во-первых, видео часто подтормаживало. Причина в ограниченном размере области предзагрузки. После ее заполнения программа переходила к загрузке остальной части файла в случайном порядке. И если по мере просмотра какой-то фрагмент для предзагрузки запрашивался со слишком медленного клиента, он не успевал загрузиться вовремя.

Увеличение области предзагрузки означало и увеличение времени ожидания перед началом просмотра.

Во-вторых, в этой схеме не работает перемотка видео. Вы что-то не расслышали? Вернуться на 10 секунд назад не сможете. И было бы не так страшно, если бы перемотку в принципе отключили. Но при попытке перемотать видео оно сбрасывалось к началу, что особенно печально, если вы уже посмотрели половину фильма. После сброса спасало проигрывание просмотренного фрагмента на большой скорости. Либо ожидание полного скачивания.

Потом я сообразил, что можно запустить два плеера одновременно: VLC на большой скорости без звука, чтобы обеспечить последовательную загрузку данных, и обычный плеер с незавершенным файлом. И, наконец, я выставил в параметрах мю-торрента размер области предзагрузки заведомо больше размера файла (параметр streaming.min_buffer_piece), чтобы она никогда не заполнялась.

Итоговая схема:

• запускаешь торрент на скачивание;
• нажимаешь на кнопку «Поток»;
• открываешь файл в обычном плеере.

На втором шаге, благодаря завышенному размеру области предзагрузки, VLC никогда не запускался, а файл загружался последовательно. На самом деле схема чуть сложнее, потому что из-за какого-то бага на кнопку «Поток» приходилось нажимать дважды. Первого раза недостаточно, если в момент нажатия не скачался первый фрагмент.

Я использовал такую схему несколько лет. Но в прошлом году вышла версия мю-торрента 3.4, из которой потоковый просмотр фильмов по мере загрузки выпилили. Причем не до конца: пустое место от кнопки «Поток» реагировало на нажатие и запускало потоковую загрузку! Но из-за отключенной возможности регулировать размер области предазгрузки большой пользы в этом не было.

Нормальная реализация в qBittorrent

Некоторое время я использовал предыдущую версию с выключенными обновлениями. Но, настраивая новый ноутбук, я подумал, что пляски с бубном вокруг мю-торрента должны закончиться. Изучил аналоги и нашел программу qBittorrent. Она не такая навороченная, как мю-торрент. Но мне ее возможностей достаточно. И честная последовательная загрузка включена в штатные функции и доступна без дополнительной настройки.

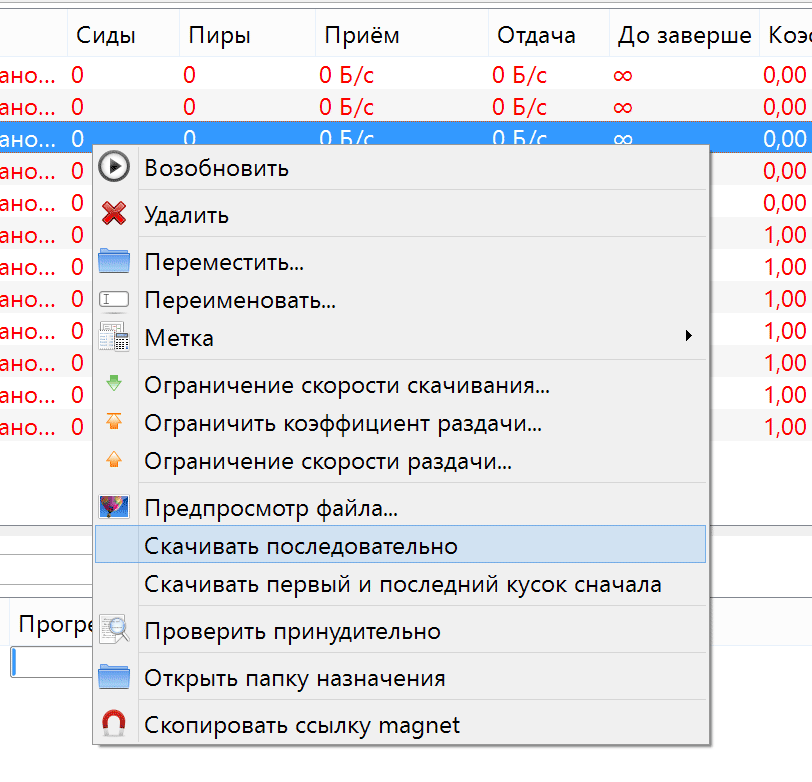
При последовательной загрузке торрентов не надо ждать окончания загрузки фильмов, если у вас быстрый интернет и если на торренте несколько сидов. Когда торрент раздается одним сидом (сразу после публикации), скорость загрузки определяется его исходящим каналом, и последовательное скачивание не поможет быстро начать смотреть видео.

А как вы скачиваете фильмы? Используете последовательную загрузку? Будете ли использовать?

Про интерфейс почты Гугла

Вот кнопки «назад» и «ответить» в веб-интерфейсе почты Гугла:

Символы на них настолько похожи, что беглый взгляд их не различает. Из-за этого я часто жму «назад» вместо «ответить».

Это самая главная проблема в текущей версии интерфейса.

Загрузка файлов перетаскиванием в Опере 12 β

Скачал и установил новую бета-версию Оперы. Среди новинок HTML5 Drag and Drop — возможность загружать файлы, перетаскивая их из проводника. Правда, в отличие от Хрома и Файерфокса, давно поддерживающих эту технологию, Опера перед загрузкой выдает модальное окно и даже не дает переключиться на другие вкладки:

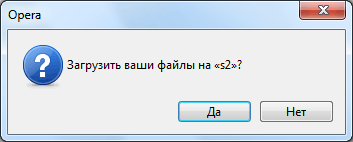
На этом, однако, удивительные вещи не заканчиваются. Оказывается, кнопка «нет» в этом модальном окне предназначена не для того, чтобы предотвратить загрузку при случайном перетаскивании файла в браузер, а для того, чтобы открыть файл в текущей вкладке вместо открытой страницы. Взрыв мозга!

Надеюсь, в окончательном выпуске уберут этот костыль, обеспечивающий обратную совместимость там, где она не нужна.

Переключатель кадров для презентаций и раздутая функциональность

Не так давно я участвовал в одной конференции. Иногда выступающие путались с беспроводным переключателем кадров презентаций. Как рассказал знакомый организатор, люди нажимают «page up» вместо «page down».

Еще оказалось, что переключатель кадров совмещен с пультом управления проектором (а проектор дополнительно соединен с ноутбуком по USB). Поэтому пульт нужно направлять на проектор, а не ноутбук. Кажется, ничего сложного в этом нет.

Когда я увидел этот пульт, я испугался.

Нужные кнопки я обвел красным. Во время выступления постоянно приходилось отвлекаться от рассказа, смотреть на этот чертов пульт, чтобы случайно не нажать куда-нибудь не туда и не выключить проектор или хрен знает что с ним сделать. А еще пульт нужно держать не как попало, а направлять на проектор. И еще в другой руке держать лазерную указку. И у нее тоже есть кнопочка. Кошмар!

Вот каким должен быть переключатель кадров, совмещенный с лазерной указкой.

Достаточно всего трех кнопок: вперед, назад и лазерный луч. Ошибиться с кнопкой трудно. Даже если случайно переключить кадр, соседняя кнопка быстро исправит дело. Мне попадались подобные устройства. Ими начинаешь пользоваться практически сразу и без ошибок.

В чем мораль этой истории? В том, что продукт должен решать только одну задачу, и в него не надо включать посторонние функции. Если бы разработчики проектора разместили на пульте только кнопки включения и настройки, организаторам пришлось бы достать нормальный переключатель кадров и обеспечить выступающим комфортные условия.

Раздутая функциональность посредственного продукта не дает людям пользоваться нормальными вещами.

Восстановление текстов в новой версии S2

В новой версии движка S2, которую я выпустил вчера, появилось очень важное нововведение. Теперь он умеет восстанавливать несохраненные тексты после непредвиденных ситуаций вроде зависаний или падений браузера, случайного закрытия окна и т. д.

Интерфейс простой. При следующем входе в админку выводится вот такое сообщение:

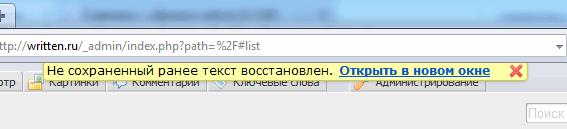
Восстановленный текст из нового окна можно затем скопировать куда угодно.

Реализация тоже крайне простая. Каждые 5 секунд содержимое редактора отправляется в HTML5-хранилище (которое localStorage) и удаляется во время сохранения. При входе в админку отображается сообщение, показанное выше, если в хранилище что-то есть.

С помощью этого способа (в отличие от автосохранения) мы оставляем пользователю контроль над тем, когда сохранять редактируемый текст, но избавляемся от проблемы утери несохраненного текста при компьютерных сбоях или непродуманных действиях пользователя.

Совместное редактирование без блокировок

Рассмотрим ситуацию, когда над неким сайтом (или другим проектом) работает коллектив авторов, и подумаем над такой задачей: как обеспечить возможность совместного редактирования документов.

Если над такой возможностью вообще не задумываться, то в ситуации, когда два автора начинают редактировать один и тот же документ, правки одного из авторов скорее всего потеряются.

Эту проблему можно решать при помощи блокировок, как сделано, например, в движке DokuWiki. Когда документ открыт для редактирования одним пользователем, другим пользователям запрещено его редактировать.

Едва ли решение с блокировками можно признать удачным. Если автор начинает редактировать документ, а потом отвлекается, нужно отбирать блокировку по по истечению какого-либо времени (в DokuWiki, кажется, 15 минут), чтобы документ не остался заблокированным навечно. Тогда изменения отвлекшегося автора могут быть утеряны.

Я придумал другой метод, который собираюсь реализовать в своем движке сайтов S2. Этот метод особенно оправдан, если совместное редактирование возникает достаточно редко. Например, редактор должен внести небольшие исправления в документ, написанный автором.

В таких ситуациях вместо надоедливых сообщений о блокировках нужно просто проверять, изменялся ли документ другими пользователями в промежутке между открытием и сохранением. Если изменялся, мы не сохраняем документ, и выводим пользователю сообщение о том, что он должен открыть новую версию документа и самостоятельно перенести туда дописанные фрагменты текста.

Блокировки держат пользователя в напряжении (нельзя отвлекаться больше, чем на 15 минут) и не решают задачу совместного редактирования до конца: всё равно остается возможность возникновения конкурирующих правок. В моем методе ничто без надобности не отвлекает пользователя от его задач.

Запись диска

Экран программы записи дисков из Windows 7:

Абрам Абрамович Абрамович из села Тавтология, ага.

Google Reader

На протяжении нескольких лет я читал RSS в Яндекс.Ленте. Мне приходилось пользоваться разными компьютерами, в том числе и чужими. Поэтому мне нужна была онлайн-читалка. Я выбрал Яндекс.Ленту, а не Google Reader, так как сервисами Яндекса пользовался чаще.

Иногда Я.Л глючила. То открытым текстом писала о каких-то проблемах. То говорила, что я ни на что не подписан. Впрочем, глюки исчезали достаточно быстро и возникали не так часто, чтобы доставлять неудобства.

Примерно полгода назад глюки стали более серьезными. Многократное обновление страницы не помогло. Вместо отображения подписок Я.Л настойчиво предлагала создать новую ленту. Я нажал на эту ссылку. Видимо, зря, потому что с тех пор я своих подписок больше не видел.

Я понял, что пришла пора прощаться с Яндекс.Лентой, и перебрался на Гугл Ридер. По бекапам многолетней давности, истории браузера и воспоминаниям кое-как восстановил те RSS, на которые был подписан.

Раз уж зашла речь, не могу не прокомментировать интерфейс Гугл Ридера. Сказать, что его делал программист, а не дизайнер — не сказать ничего. Любой, кто пользовался Яндекс.Лентой, легко назовет его недостатки.

(Здесь, конечно, достаточно было бы привести два скриншота, но после глюков Лента пуста, и добавлять что-либо туда мне не хочется. Придется ограничиться замечаниями.)

Во-первых, верхняя часть страницы не прокручивается. 132 пикселя бесценного расстояния по вертикали расходуются на всякие ненужные панели.

Во-вторых, под каждой записью находятся отвлекающие никому не нужные синие ссылки-кнопки. За полгода только один раз я воспользовался ссылкой «Отправить по эл. почте».

В-третьих, чтобы опознать автора записи, нужно отыскать синюю строчку под заголовком (тоже синим) и прочитать ее (а синий текст читается хуже черного). В Яндекс.Ленте слева от записей отображается аватарка автора, прописанная в RSS картинка или favicon сайта; при этом несколько идущих подряд записей с одного сайта группируются и снабжаются только одной картинкой. В таких условиях достаточно беглого взгляда на страницу, чтобы распознать авторов записей.

Сейчас к Гугл Ридеру я привык, перечисленные недостатки мешают не так, как в самом начале. Да и работает он стабильно (в отличие от Яндекс.Ленты). За всё время использования не глючил ни разу. Но всё-таки хотелось бы, чтобы у хорошего продукта был хороший интерфейс. Ведь это же несложно, не так ли?

Про мю-торрент

Что-то в последних версиях мю-торрента перемудрили с интерфейсом.

Мыши будущего

Сегодня задумался о том, какими могут быть мыши будущего. Разумеется, если технологии, содержащие в названии корень «тач», их не вытеснят.

Основная идея заключается в том, что через мышь нужно делать обратную связь в интерфейсах. Сам по себе курсор должен перемещаться легко; а если я, например, перетаскиваю окно, коэффициент трения между мышью и столом должен увеличиться. Технически это сделать несложно, из мыши при необходимости может выдвигаться какая-нибудь резиновая деталь, касающаяся стола.

Можно пойти дальше и сделать регулировку силы нажатия на кнопки в зависимости от положения курсора. Например, при удалении файлов в диалоге подтверждения кнопка «Ok» должна нажиматься труднее кнопки «Отмена».

И, наконец, пределом мечтаний является колесо прокрутки, которое нельзя продолжать крутить после того, как мы уже дошли до конца или начала документа.

Странности фотошопа

Я постоянно спотыкаюсь в фотошопе на этом окне из-за нечеловеческого не принятого в Windows порядка кнопок.

Nokia PC Suite

Ну почему софт, поставляемый вместе с девайсами вроде фотоаппаратов и телефонов, настолько кривой?

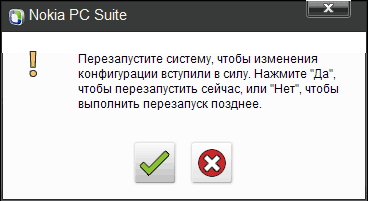
Press any key to continue or any other key to exit, ага.

Каким мог быть веб

В недавней статье на Спектаторе Дима Смирнов рассуждает о гипертексте и вебе. Примерно в стиле «как всё сейчас плохо и как могло бы быть хорошо». Вот, например:

Основная проблема еще и в том, что в идеале гипертекст не только читается нелинейно, но и пишется нелинейно. Инструментов для этого практически нет. Да и всяких полезных штук в языке на этот случай — тоже.

…

Вообще же надо «пинать» не только html, но и всё в целом. Браузер по определению (browser) — средство навигации. Сейчас из навигации в браузерах есть только кнопки «вперед-назад», а крутизна браузера зависит от того, как хорошо он рендерит страницы.

Однако такие рассуждения не новы. Мысли из серии «каким мог быть веб» в большом количестве встречаются у Якоба Нильсена. Вот цитата из его книги про веб-дизайн:

Средства поиска по всему Интернету должны быть интегрированы с броузером, чтобы иметь возможность поиска по заданному набору сайтов, который предпочитает пользователь, или по страницам, которые он уже посетил. Как часто вы пытаетесь найти что-то, что вы точно видели в Интернете? Если бы вы могли сказать об этом поисковому устройству, проблема поиска заметно бы упростилась (ведь каждый отдельный пользователь может посетить от нескольких тысяч до миллиона страниц, при том, что на самом деле их миллиарды).

Технологии и сервисы не стоят на месте. Идея «поиска по посещенным сайтам» Нильсена реализована (правда, в несколько измененном виде) в Яндекс.Ленте. В этой онлайновой RSS-читалке сделан поиск по RSS-каналам, на которые подписан пользователь. Таким образом я всегда могу очень быстро найти прочитанные через Яндекс.Ленту сообщения.

О пульте лифта

Захожу вчера в лифт. «Продвинутый» — кнопочки с номерами этажей в нем удерживаются в нажатом состоянии, пока лифт не доедет до нужного этажа. Нажимаю кнопку четвертого этажа. Кнопка нажалась, а лифт не едет. Спустя некоторое время я понял, что произошло. Я зашел в лифт на четвертом этаже.

Что нужно говорить в таких случаях? Правильно. Интерфейс пульта лифта не продуман. Мало того, что на нем больше десяти кнопок, а в здании — пять этажей. И даже того, что текущий этаж никак не выделен. Там кнопка, соответствующая текущему этажу, нажимается и удерживается в нажатом состоянии, а лифт не едет.

Привет дизайнерам интерфейсов Микрософта!

Вот контекстное меню Excel 2007:

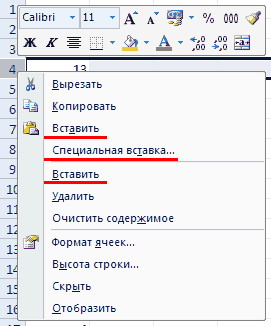
Три команды со вставкой для отсутствующих мозгов юзера — это слишком!