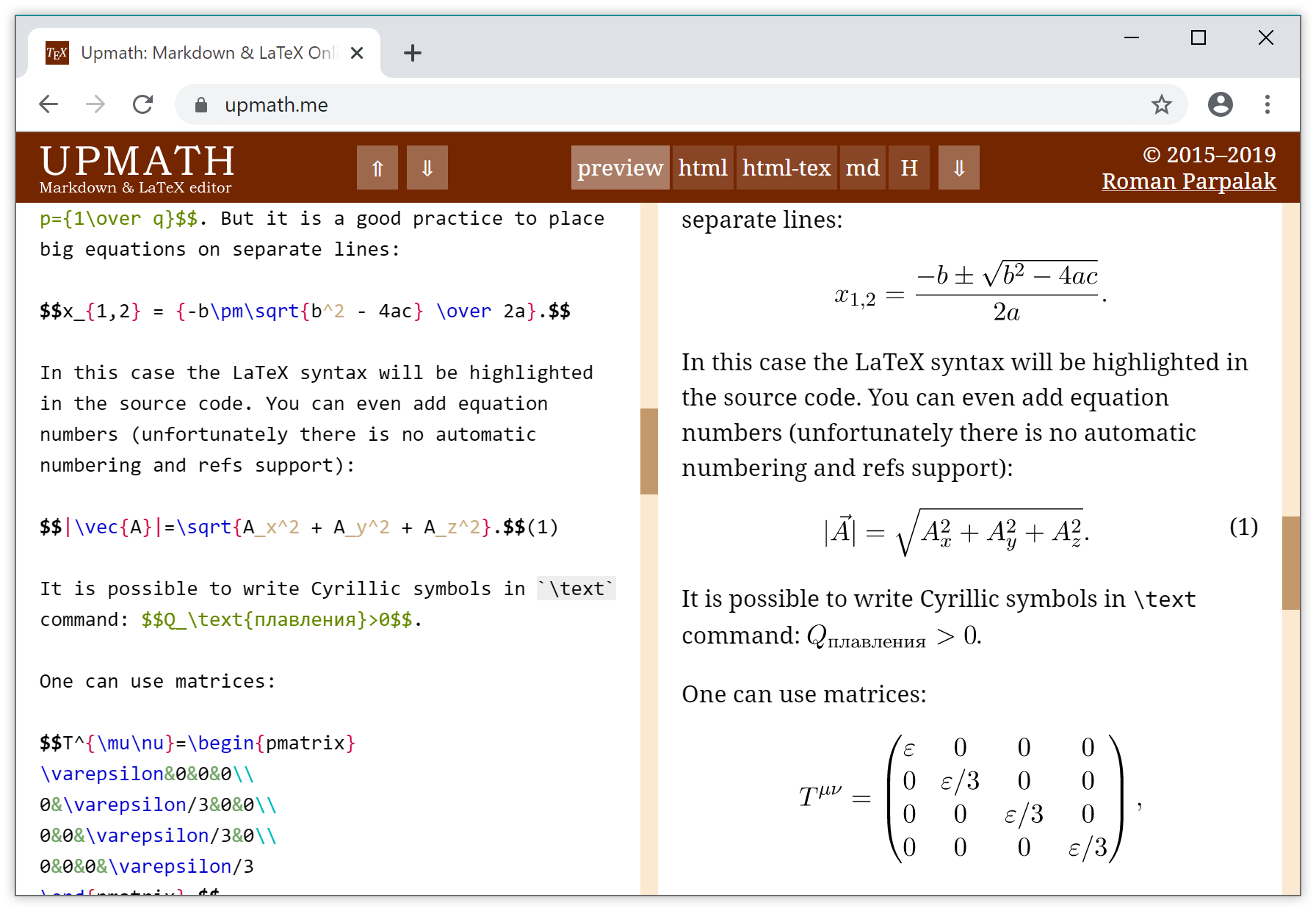
upmath
Upmath — это редактор математических текстов для интернета. Оформляете текст в маркдауне, пишете формулы на латехе, а Upmath выдает
Статьи по этой теме:
Латех и
Нативное gzip-сжатие в JS
Я недавно закрыл тикет на гитхабе, который висел с 2017 года. Его автор обращал внимание на длинные адреса картинок в моем сервисе математических формул. С 2023 года нативное сжатие произвольных данных в JS стало доступным во всех основных браузерах, и с его помощью я сделал вариант сжатых адресов.
Давние читатели вспомнят, что я уже рассказывал об адресах картинок, и даже упоминал об этом тикете. Повторю, что для использования в вебе формулы, например, $$a^2+b^2=c^2$$, её исходник на латехе a^2+b^2=c^2 кодируется через проценты (RFC 3986) и подставляется в URL:
//i.upmath.me/svg/a%5E2%2Bb%5E2%3Dc%5E2Кодирование через символы процента очень неэкономное, поэтому и без того длинный код изображений и диаграмм становится ещё больше. Адрес $$a^2+b^2=c^2$$ в новой схеме выглядит так:
//i.upmath.me/svgb/S4wz0k6KM7JNjjMCAAЗдесь вместо кодирования через проценты используется сжатие deflate (тот же алгоритм, что и в gzip) и кодировка, аналогичная base64. Вот рабочий пример кода, который делает такое преобразование:
function deflateRaw(text, callback) {
if (typeof CompressionStream === 'undefined') {
callback(null);
return;
}
try {
var stream = new Blob([text]).stream();
var compressedStream = stream.pipeThrough(new CompressionStream('deflate-raw'));
new Response(compressedStream).blob().then(function (compressedBlob) {
return compressedBlob.arrayBuffer();
}).then(function (buffer) {
var compressedArray = new Uint8Array(buffer);
var binary = Array.from(compressedArray).map(function (b) {
return String.fromCharCode(b);
}).join('');
var base64 = btoa(binary).replace(/\+/g, '-').replace(/\//g, '_').replace(/=+$/, '');
callback(base64);
}).catch(function () {
callback(null);
});
} catch (e) {
callback(null);
}
}
function getImgPath(formula, callback) {
var fallbackUrl = '//i.upmath.me/svg/' + encodeURIComponent(formula);
deflateRaw(formula, function (compressed) {
var shortUrl = compressed ? '//i.upmath.me/svgb/' + compressed : null;
callback(shortUrl && shortUrl.length < fallbackUrl.length ? shortUrl : fallbackUrl);
});
}
Важная особенность API браузеров по сжатию заключается в его асинхронности. Мы не можем получить результат сжатия в той же функции, в которой его инициируем. API возвращает promise, который «разрешится» позднее. Чтобы обеспечить обратную совместимость и откатываться к несжатым адресам в старых браузерах, я проверяю саму поддержку CompressionStream и перехватываю возможные исключения. Также для обратной совместимости результат возвращаю через вызов пользовательского коллбэка, а не в виде промиса.
Вот пример того, как с вышеприведенным кодом создать картинку с формулой:
var node = document.createElement('img');
getImgPath('a^2+b^2=c^2', function(path) {
node.setAttribute('src', path);
});
Стоит отметить, что сам алгоритм сжатия deflate был давно портирован на JS, поэтому при необходимости можно было использовать сторонние библиотеки, например, pako. Кроме того, код библиотек работает синхронно, так что ни о каких коллбэках и промисах думать не нужно. В моём же случае я не хотел в
Оценим результат на примере диаграммы из предыдущей заметки. Длина старого несжатого URL равна 6,3 килобайт, а сжатого — 1,3 килобайт, что почти в 5 раз короче.
Сложение вращений и анимация в TikZ
В рекомендациях ютуба мне часто попадалась задачка о вращающихся окружностях. Вот её формулировка: окружность катится без проскальзывания по другой окружности втрое большего радиуса и совершает вокруг неё один оборот. Сколько оборотов при этом она совершит вокруг своего центра?
Эта задача встречалась в американском тесте абитуриентов 1982 года и примечательна тем, что среди предложенных вариантов ответов не было правильного. Сама задача, её история и связанные вопросы разобраны в этом видео:
Я вспомнил об этой задаче, потому что, наконец, разобрался как делать анимации в TikZ, и теперь вместо множества слов могу просто показать анимированные иллюстрации.
В этой задаче кажущийся ответ — три оборота — неправильный. Оборотов будет на 1 больше, чем отношение радиусов. В этом можно убедиться напрямую, просто подсчитав количество оборотов. Я сомневаюсь, что
$$\dvisvgm\definecolor{cyan}{RGB}{0, 200, 250} \shorthandoff{"} \usetikzlibrary {shapes.geometric} \usetikzlibrary{animations} \begin{tikzpicture} \def\a{1} \def\b{3} \useasboundingbox (-\b-2*\a-0.1,-\b-2*\a-0.1) rectangle (\b+2*\a+0.1,\b+2*\a+0.1); \draw[cyan,very thin] (-\b-2*\a,-\b-2*\a) grid (\b+2*\a,\b+2*\a); \node[star,star points=57, star point ratio=1.07,minimum size=6.2cm, draw,fill=white] at (0,0); \draw[purple,fill] (0:\b) circle (1pt) -- (0,0) circle (1pt) node [midway, sloped, above] {$\b$} ; \begin{scope}:rotate = {0s="0", (5*\b)s="360",repeats} \begin{scope} :rotate = {0s="0", (5*\a)s="360", origin={(\b+\a,0)}, repeats} \node [star,star points=19, star point ratio=1.2,minimum size=2.2cm, draw,fill=white] at (0:\b+\a) {}; \draw [purple,fill] (0:\b+\a) circle (1pt) -- (0:\b) circle (1pt) node [midway, sloped, above] {$\a$} ; \end{scope} \end{scope} \coordinate (A) at (1,1.5); \node [fill=white,inner sep=1pt,anchor=east,xshift=3pt,yshift=-1pt] at (A) {$\text{обороты: }\,\,\,.$}; \foreach \t in {3,2,...,0} { \node :opacity = { 3.75*(0) s="0", 3.75*(0+\t) s="0", 3.75*(0.001+\t) s="1", 3.75*(0.999+\t) s="1", 3.75*(1+\t)s="0", 3.75*(4) s="0", repeats } [anchor=east,inner sep=1pt] at (A) {$\t$}; } \foreach \t in {0,1,...,9} { \node :opacity = { 0.375*(0) s="0", 0.375*(0+\t) s="0", 0.375*(0.01+\t) s="1", 0.375*(0.99+\t) s="1", 0.375*(1+\t)s="0", 0.375*(10) s="0", repeats } [anchor=west,inner sep=1.5pt] at (A) {$\t$}; } \end{tikzpicture}$$
Конечно, задачу можно решить стандартным геометрическим подходом: рассмотреть углы между радиусами к точкам касания в начальном и текущем положениях, и приравнять длины дуг между этими точками. Но как быть, если задачу надо решить в уме? Ход рассуждений может быть следующим.
Представим оборот меньшей окружности вокруг большей как сумму двух движений. В первом движении окружности вращаются так, что их центры остаются неподвижными. В этом случае малая окружность действительно совершит три оборота, пока большая окружность совершает один оборот. Второе движение — это вращение обеих окружностей, соприкасающихся в одной точке, на ещё один оборот. При сложении двух движений обороты большой окружности оказываются разнонаправленными и компенсируются, а обороты малой окружности — однонаправленными и суммируются, то есть малая окружность совершит четыре оборота. На следующей иллюстрации этой идеи легко подсчитать количество оборотов каждой окружности в полном цикле:
$$\dvisvgm\definecolor{cyan}{RGB}{0, 200, 250} \usetikzlibrary {shapes.geometric} \usetikzlibrary{animations} \begin{tikzpicture} \def\a{1} \def\b{3} \useasboundingbox (-\b-2*\a-0.1,-\b-2*\a-0.1) rectangle (\b+2*\a+0.1,\b+2*\a+0.1); \draw[cyan,very thin] (-\b-2*\a,-\b-2*\a) grid (\b+2*\a,\b+2*\a); \begin{scope}:rotate = {0s="0", 5s="-360", 6s="-360", 11s="0", 12s="0", repeats} \node[star,star points=57, star point ratio=1.07,minimum size=6.2cm, draw,fill=white] at (0,0); \draw[purple,fill] (0:\b) circle (1pt) -- (0,0) circle (1pt) node [midway, sloped, above] {$\b$} ; \end{scope} \begin{scope} :rotate = {0s="0", 6s="0", 11s="360", 12s="360", origin={(0,0)}, repeats} \begin{scope} :rotate = {0s="0", 5s="1080", 6s="1080", 11s="1080", 12s="1080", origin={(\b+\a,0)}, repeats} \node [star,star points=19, star point ratio=1.2,minimum size=2.2cm, draw,fill=white] at (0:\b+\a) {}; \draw [purple,fill] (0:\b+\a) circle (1pt) -- (0:\b) circle (1pt) node [midway, sloped, above] {$\a$} ; \end{scope} \end{scope} \end{tikzpicture}$$
RSS, формулы и Feedly
Постоянные читатели помнят, что у меня есть сервис по превращению математических формул в картинки и редактор для создания математических текстов. С заменой формул на картинки на обычных
Еще в 2011 году я стал отдавать в RSS растровые картинки, потому что непонятно, в каком окружении будет отображаться контент оттуда. А на обычных
Когда в 2013 году прекратила работать
У Feedly была одна особенность с отображением картинок: они принудительно становились плавающими (включалось
Сейчас я решил проверить, не научился ли Feedly отображать нормально картинки. Оказалось, что научился. Если вы читаете этот текст через RSS в Feedly, можете в этом убедиться в предыдущем абзаце.
Чтобы два раза не вставать, я попросил ChatGPT составить
<?xml version="1.0" encoding="UTF-8"?>
<xsl:stylesheet version="1.0" xmlns:xsl="http://www.w3.org/1999/XSL/Transform">
<xsl:template match="/">
<html>
<head>
<title><xsl:value-of select="rss/channel/title" /></title>
<style type="text/css">
a {
color: #56d;
text-decoration-thickness: 1px;
text-decoration-color: rgba(85, 102, 221, 0.5);
}
body {
max-width: 720px;
font: 16px/1.5 sans-serif;
margin: 0 auto;
}
h1, h2, h3 {
margin: 1em 0 0.25em;
}
p {
margin: 0 0 0.75em;
}
</style>
</head>
<body>
<h1>
<a href="{rss/channel/link}">
<xsl:value-of select="rss/channel/title" />
</a>
</h1>
<xsl:for-each select="rss/channel/item">
<div class="item">
<h2><a href="{link}"><xsl:value-of select="title" /></a></h2>
<div><xsl:value-of select="description" disable-output-escaping="yes" /></div>
</div>
</xsl:for-each>
</body>
</html>
</xsl:template>
</xsl:stylesheet>
Чтобы это заработало, нужно добавить ссылку на такой
<?xml version="1.0" encoding="utf-8"?>
<?xml-stylesheet href="/_styles/rss.xslt" type="text/xsl"?>
<rss version="2.0">
<channel>
...
</channel>
</rss>
Кстати, пока со всем этим возился, обнаружил, что в RSS сломалось отображение исходного кода: перестало работать сохранение переносов строк внутри тегов <pre><code>. Долго пытался понять, где ошибка, пока не осознал, что это сломался сам Feedly. Похоже, эта проблема наблюдается в любых источниках в Feedly за последние недели две. Заодно сейчас и проверим, нормально ли будет отформатирован код в этой заметке.
В заключение полезный совет: если хотите отладить RSS и не хотите ждать, пока Feedly проиндексирует новую запись, можете на экране добавления нового источника добавить в URL не меняющую смысла часть запроса. Тогда Feedly распарсит RSS на лету и отобразит три последних записи:
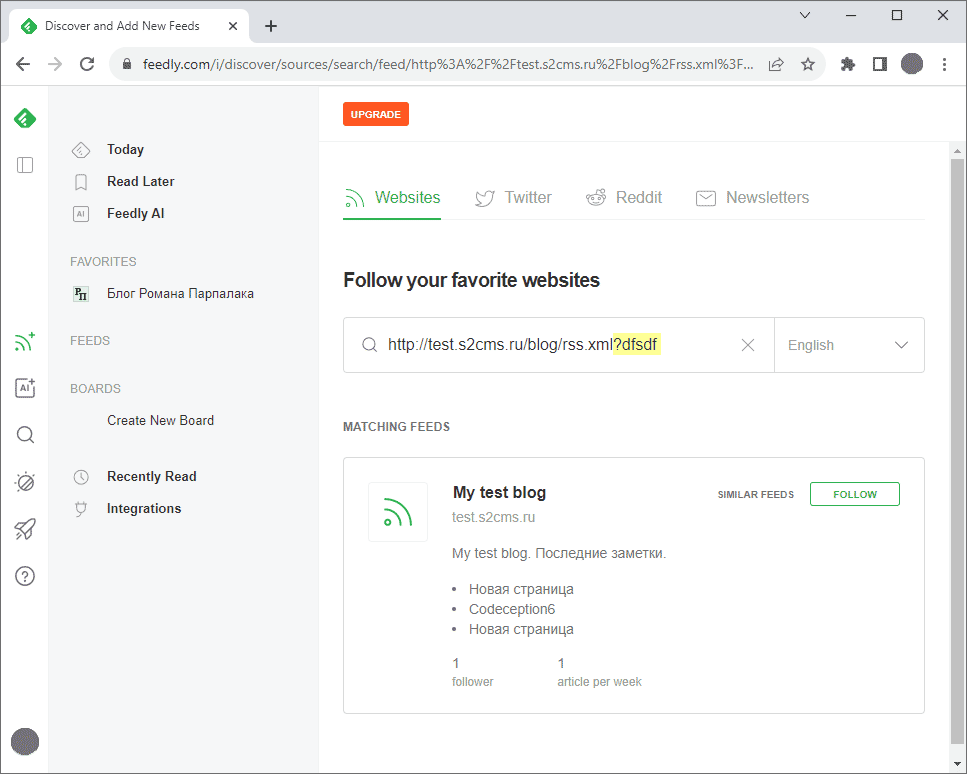
Добавлено позднее: оказывается, Feedly нормально отображает картинки только в
Воспринимайте слова в переписке буквально
В общении между людьми есть проблема недопонимания. Говорящий не всегда правильно подбирает слова, а слушающий додумывает. Иногда получается, что имели в виду одно, сказали другое, а поняли третье.
В устном общении есть возможность задать уточняющий вопрос, и проблема часто снимается. В переписке с этим сложнее, поэтому особенно важно следить за словами: проверять, правильно ли слова передают смысл, и воспринимать слова буквально.
Смотрите, что получается, если
Во всех адресах и примерах использования «https:»почему-то исчезло. Так что адреса формально неправильные.
Чтобы не отправлять вас по ссылкам, поясню, что сервис предлагает УРЛы картинок в виде //i.upmath.me/svg/f(x) и код встраивания скрипта <script src="//i.upmath.me/latex.js"></script>.
Дело в том, что схема (http или https для веба) — необязательная часть адреса, его можно опустить (см.
Посетитель вложил в свою мысль целых два неверных утверждения. Первое: https
Если бы посетитель спросил, почему так сделано, я бы ответил, и может быть даже погуглил за него. Но вопроса не было, поэтому в своем ответе я задал уточняющие вопросы:
Это вопрос или предложение? Почему вы считаете, что «https:» исчезло?
Первая часть — отсылка к технике продуктивной переписки «общаться вопросами и предложениями». Непонятно, интересовался ли посетитель, почему так сделано, или предлагал сделать
Закрепим рекомендации:
- Когда вы пишете сообщение в мессенджере или почте, перечитайте перед отправкой и проверьте, что сообщение отражает вашу мысль.
- Когда вы получили сообщение, воспринимайте его буквально, не додумывайте за автора. Если автору нужно было другое, он переспросит.
- Отвечайте на явно сформулированные вопросы. Прокомментируйте предложения: будем ли мы делать то, что предлагается, и если нет, то почему.
- Если ни вопросов, ни предложений нет, а от вас требуется реакция, и вы не знаете, что ответить, так и напишите: «Я не понимаю, в чем твой вопрос и что ты предлагаешь».
Редактор математических текстов Mathcha
Искал
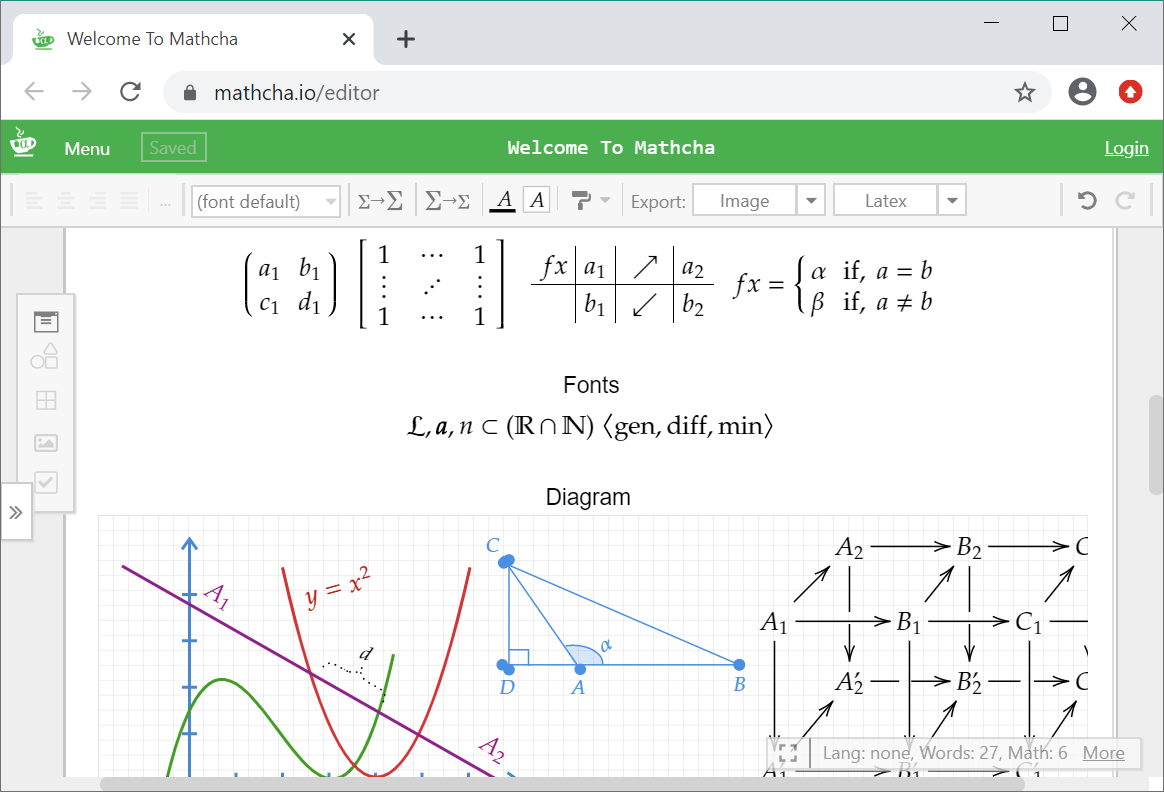
Этот редактор — визуальный: вы сразу редактируете документ вместе с форматированием. В отличие от моего редактора Upmath, в котором вы редактируете исходник на маркдауне и латехе, хотя и сразу видите результат.
Вот рисунок, который я сделал с помощью Mathcha. Накидал основу в нем, экспортировал в TikZ и подправил исходный код уже в UpMath.
$$ \tikzset{every picture/.style={line width=0.75pt}} %set default line width to 0.75pt \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1] %uncomment if require: \path (0,300); %set diagram left start at 0, and has height of 300 %Shape: Boxed Line [id:dp7642567693966007] \draw (130,80) -- (130,140) ; %Shape: Boxed Line [id:dp02318954146147889] \draw (130,150) -- (130,180) ; %Shape: Boxed Line [id:dp4638027067588357] \draw (130,190) -- (130,250) ; %Shape: Wave [id:dp03622557580885122] \draw [color={rgb, 255:red, 74; green, 144; blue, 226 } ,draw opacity=1 ] (215,80) .. controls (202.19,83.1) and (190,86.06) .. (190,89.5) .. controls (190,92.94) and (202.19,95.9) .. (215,99) .. controls (227.81,102.1) and (240,105.06) .. (240,108.5) .. controls (240,111.94) and (227.81,114.9) .. (215,118) .. controls (202.19,121.1) and (190,124.06) .. (190,127.5) .. controls (190,130.94) and (202.19,133.9) .. (215,137) .. controls (227.81,140.1) and (240,143.06) .. (240,146.5) .. controls (240,149.94) and (227.81,152.9) .. (215,156) .. controls (202.19,159.1) and (190,162.06) .. (190,165.5) .. controls (190,168.94) and (202.19,171.9) .. (215,175) .. controls (227.81,178.1) and (240,181.06) .. (240,184.5) .. controls (240,187.94) and (227.81,190.9) .. (215,194) .. controls (202.19,197.1) and (190,200.06) .. (190,203.5) .. controls (190,206.94) and (202.19,209.9) .. (215,213) .. controls (227.81,216.1) and (240,219.06) .. (240,222.5) .. controls (240,225.94) and (227.81,228.9) .. (215,232) .. controls (202.19,235.1) and (190,238.06) .. (190,241.5) .. controls (190,244.57) and (199.7,247.26) .. (210.89,250) ; %Straight Lines [id:da008457960885399407] \draw (190,80) -- (190,250) ; %Flowchart: Summing Junction [id:dp09695643217509597] \draw (135,132.75) .. controls (135,128.75) and (138.36,125.5) .. (142.5,125.5) .. controls (146.64,125.5) and (150,128.75) .. (150,132.75) .. controls (150,136.75) and (146.64,140) .. (142.5,140) .. controls (138.36,140) and (135,136.75) .. (135,132.75) -- cycle ; \draw (137.2,127.62) -- (147.8,137.88) ; \draw (147.8,127.62) -- (137.2,137.88) ; %Shape: Inductor [id:dp3454355331692156] \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; %Straight Lines [id:da4690178114375858] \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165.5) -- (130,185) -- (190,165) ; %Straight Lines [id:da10916309009890135] \draw [dash pattern={on 0.84pt off 2.51pt}] (45,164.5) -- (130,145) -- (190,165) ; % Text Node \draw (112,127) node [anchor=north west][inner sep=0.75pt] [align=left] {A}; % Text Node \draw (112,191) node [anchor=north west][inner sep=0.75pt] [align=left] {B}; \end{tikzpicture} $$
Кеширование в nginx
В прошлый раз мы рассмотрели, как в теории работает кеш и какие ошибки обычно совершают при его программировании. В этот раз я расскажу, как с помощью нескольких настроек nginx включить кеширование прямо на уровне
Я уже писал о том, как работает мой сервис генерации картинок с формулами на латехе. При первом обращении к
Иногда папку с кешем приходится удалять, если она слишком сильно разрослась. Или если я вношу правки в систему, и кеш устаревает. Посетители популярных страниц генерируют множество запросов к одинаковым формулам. В кеше их нет. Nginx направляет запросы к PHP. PHP на каждую формулу вызывает консольный скрипт латеха. Раньше у меня не было защиты от того, чтобы сервер в нагруженном состоянии хотя бы не делал одно и то же много раз. Это классическое условие гонки.
Как оказалось, приемлемое решение — включить кеш в nginx и настроить блокировку. Тогда он пропускает на бэкенд разные запросы, а одинаковые выстраивает в очередь ожидания. Результат записывает в свой внутренний временный кеш и отдает всем ожидавшим клиентам.
В блоке конфигурации http указываем папку и другие параметры зоны кеша:
fastcgi_cache_path /var/data/i.upmath.me levels=1:2 keys_zone=i_upmath:10m;
fastcgi_cache_key "$scheme$request_method$host$request_uri";Обратите внимание на ключ кеширования. Я использовал обычный адрес ресурса, потому что картинки публичны и одинаковы для всех. Если у вас закрытые ресурсы, можете попробовать добавить куки в ключ. Хотя я бы не стал так делать: велик риск ошибки и утечки чужих приватных данных через кеш.
Далее в нужном location подключаем зону:
fastcgi_cache i_upmath;
fastcgi_cache_valid 200 10m;
fastcgi_cache_methods GET HEAD;
fastcgi_cache_lock on;
fastcgi_cache_lock_age 9s;
fastcgi_cache_lock_timeout 9s;Помимо кеширования здесь включена блокировка для предотвращения race condition. Длительность блокировки и ожидания я выбрал 9 секунд, потому что таймаут запуска латеха в моей системе 8 секунд. Вы можете подобрать другое значение.
На моем сервере ограниченное количество процессов
fastcgi_buffers 8 16k;
fastcgi_buffer_size 32k;
fastcgi_connect_timeout 90;
fastcgi_send_timeout 90;Технически правильное решение в моей ситуации — прогревать новый кеш, пока система работает со старым. А именно, брать часть текущего потока запросов формул, генерировать для них новые картинки и складывать в новую папку. Когда популярные формулы окажутся в новом кеше, переключать папки.
С прогревом нового кеша пользователи не заметят подмены, и сервер будет работать в комфортном режиме. Но систему прогрева нужно еще программировать. А решение с nginx внедряется простой правкой конфига. Конечно, картинки с формулами у некоторых пользователей в момент очистки кеша перестают открываться. Но для
Стили для печати и конвертация в PDF
Постоянные читатели помнят, что у меня есть двухпанельный редактор математических текстов Upmath: слева пишете текст с разметкой на маркдауне и латехе, справа получаете результат.
От пользователя пришло письмо, в котором он спрашивает, есть ли конвертация маркдауна и латеха в PDF. Вопрос задают не первый раз. Мне сообщали о
Главная задача сервиса Upmath — подготовка математических текстов для публикации в вебе. Результат его работы —
Но сейчас я задумался. Не всем нужен высококачественный PDF.
Печатать можно напрямую из браузера. Хоть на настоящем принтере, хоть в
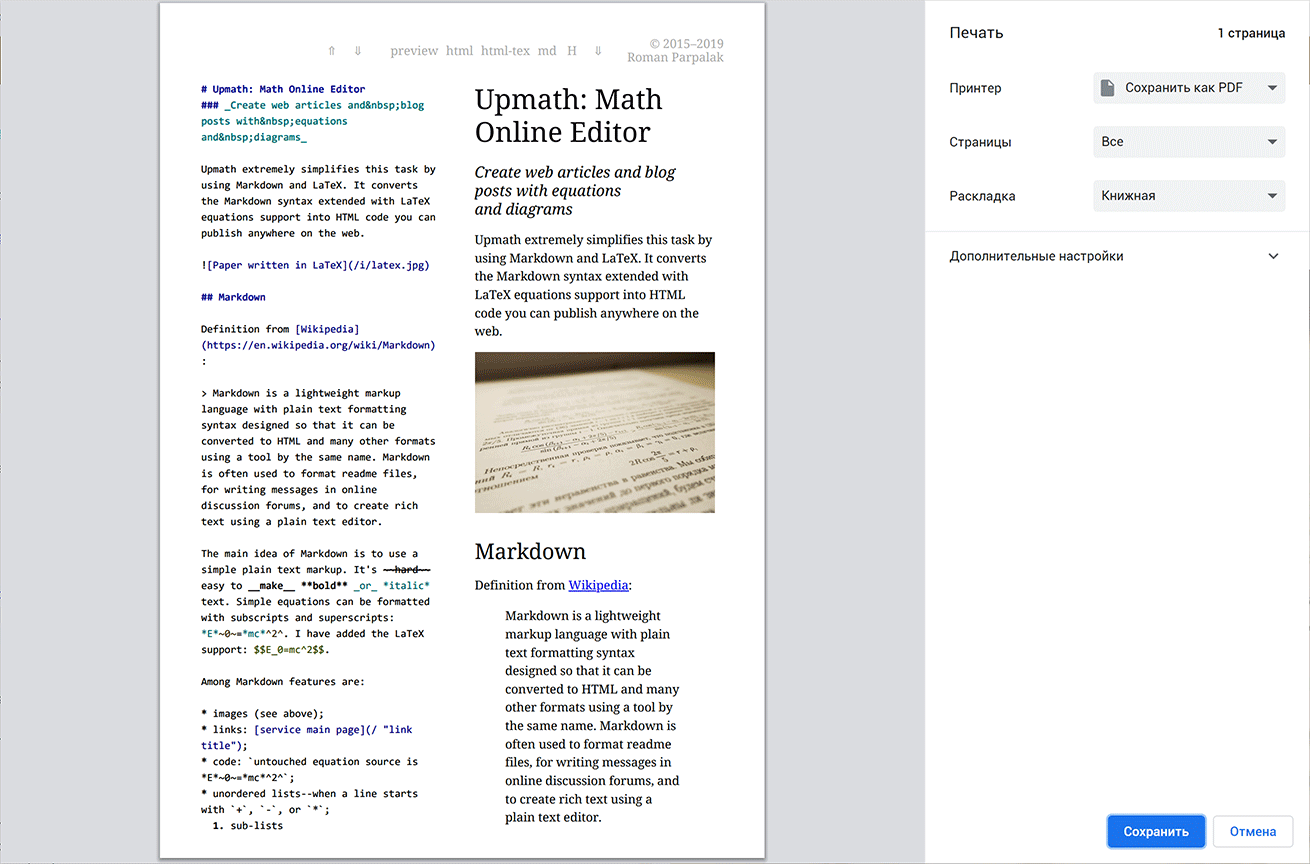
Мне ничего не стоило добавить стили для печати. Результат сразу преобразился:
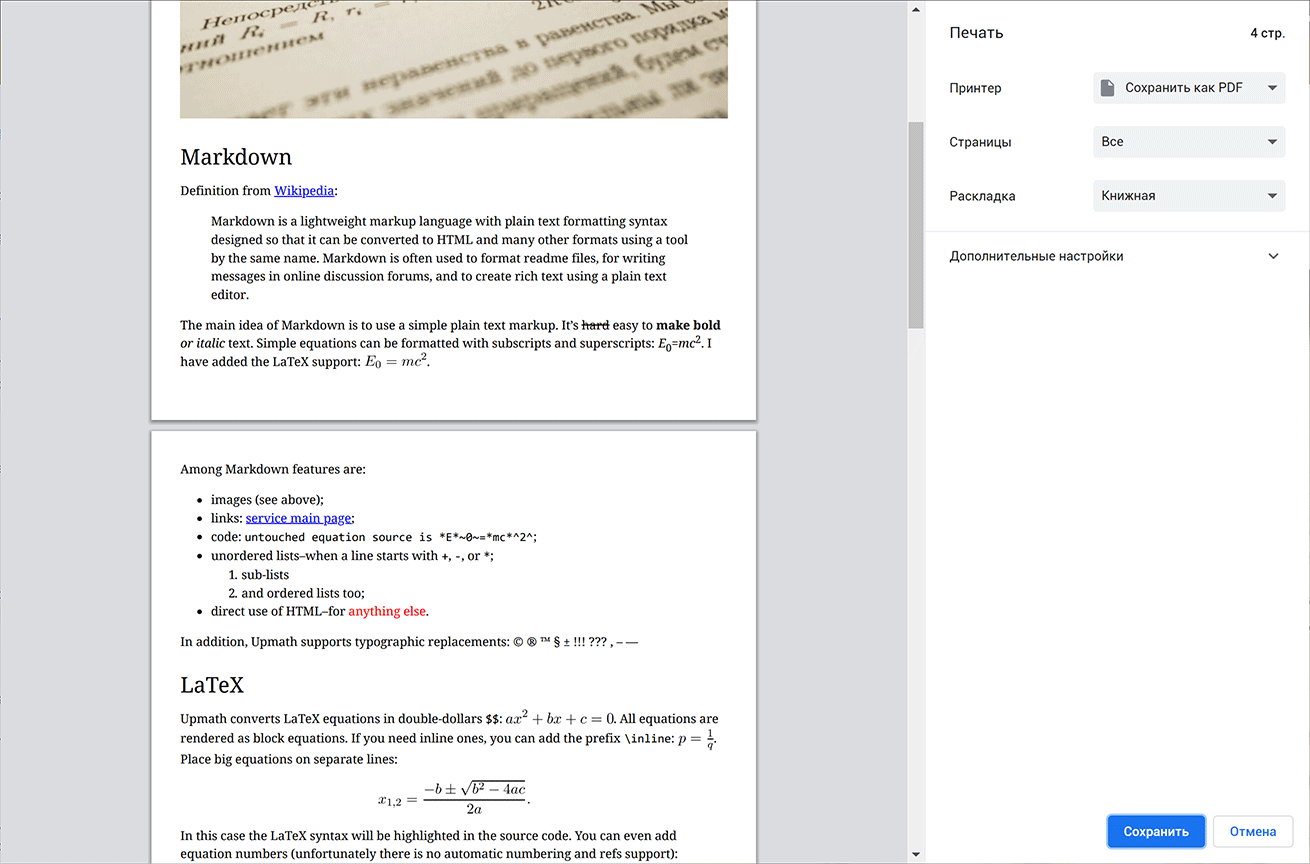
Качество получающихся документов мне не очень нравится. Я добился того, чтобы картинки не разбивались на две страницы. Но исключить разрыв страницы после заголовков у меня не получилось. Не понимаю, почему ни хром, ни FF не понимают инструкцию
h1, h2, h3 {
break-after: avoid;
}Будем ждать, пока эти баги в браузерах будут исправлены.
О схеме URL сервиса генерации картинок с формулами
В посте про объемный чертеж я привел саму картинку, но не ее код. А без кода картинка бесполезна: нельзя ни подсмотреть, как она сделана, ни изменить под свои нужды.
На самом деле код картинки содержится в ее адресе. Как писал Якоб Нильсен 19 лет назад, URL — это интерфейс. И я принял такое интерфейсное решение. Формула на латехе (например, a^2+b^2=c^2) кодируется и добавляется в урл:
//i.upmath.me/svg/a%5E2%2Bb%5E2%3Dc%5E2По нему открывается сама картинка с формулой: $$a^2+b^2=c^2$$.
Таким образом, из адреса картинки расшифровкой можно получить ее исходный код. Чтобы облегчить этот процесс, я сделал адрес другого вида (от svg остается последний символ):
//i.upmath.me/g/a%5E2%2Bb%5E2%3Dc%5E2По этой ссылке открывается
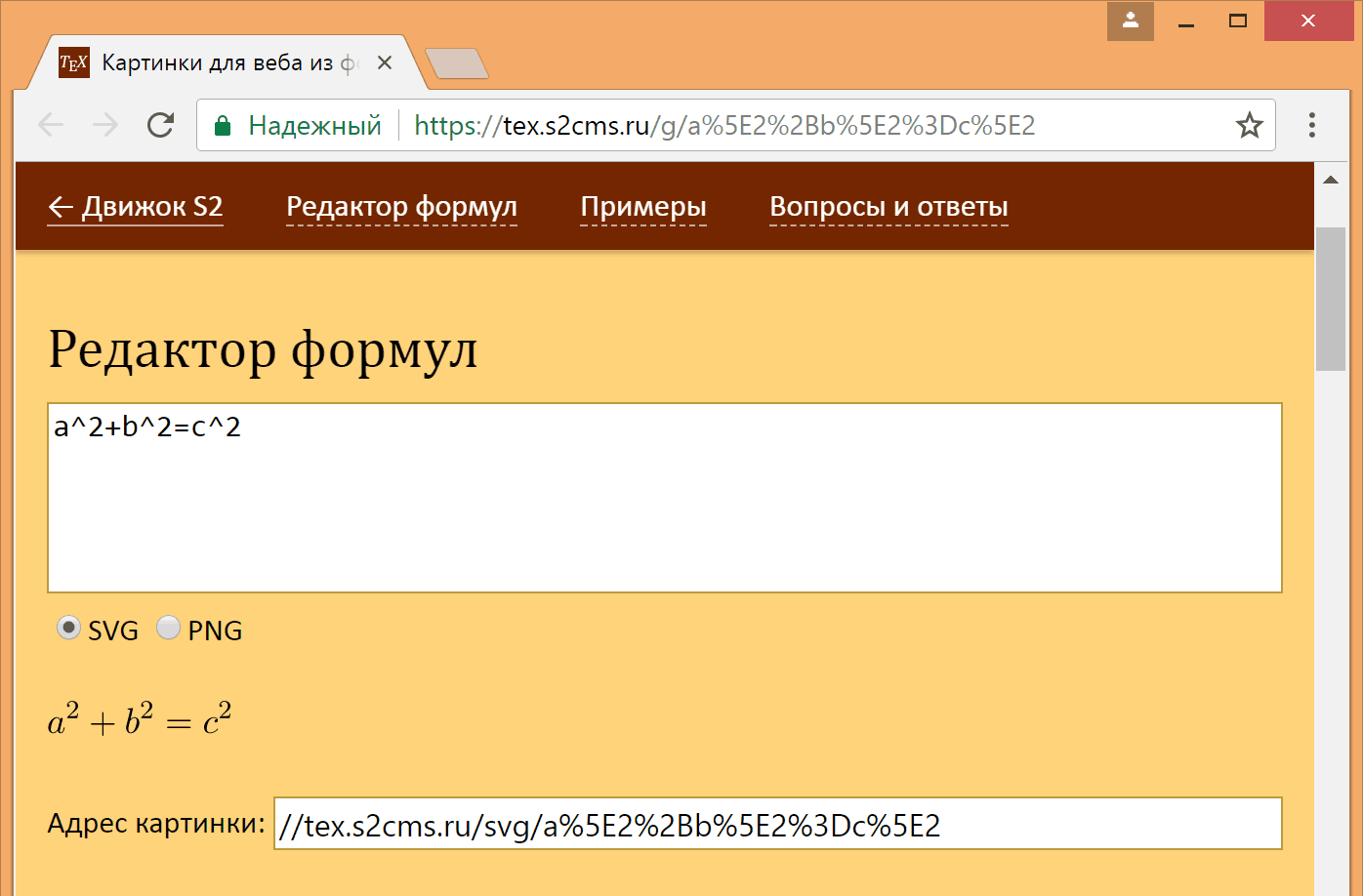
Вообще, исходный код может быть достаточно длинным. Вот пример, в котором на комплексной плоскости отмечены первые 10 степеней числа $$1+i\pi/10$$:
\begin{tikzpicture}[scale=1.0545]\small
\tikzset{>=stealth}
\def\k{10}
\def\p{3.1415926/\k}
\def\r{3.1}
\def\l{5.8}
\def\t{0.07}
\draw[->,thin,gray] (-\l,0)--(\l,0);
\draw[->,thin,gray] (0,-0.6)--(0,\l);
\draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$};
\foreach \l in {1,...,\k}
\draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)});
\draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}) node[pos=0.91,above] {$-1,\!5934+0,\!1561i$};
\draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$}
(-\r,\t)--(-\r,-\t) node[below]{$-1$}
(\t,\r)--(-\t,\r) node[left]{$1$}
(0,0) node [anchor=north west,yshift=-0.07cm] {$0$};
\draw [line width=0.21mm,opacity=0] (-\l,-0.6) rectangle (\l,\l);
\end{tikzpicture}Результат:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{10} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}) node[pos=0.91,above] {$-1,\!5934+0,\!1561i$}; \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.2mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
Этот пример я взял из статьи о формуле Эйлера $$e^{i\pi}=-1$$. Первую версию картинки рисовал вручную. В Maple выполнил возведение в степень и построил график. Открыл его в фотошопе и поверх дорисовал
На версию с графиком в tikz ушло столько же времени, или даже больше. Но масштабируемость результата находится на совершенно другом уровне. Чтобы нарисовать первым способом вдвое больше векторов, нужно потратить вдвое больше времени. Второй способ требует изменения одного числа k в исходном коде, и foreach сделает всю работу. Вот 20 векторов:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{20} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}); \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.2mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
Вот 50:
$$\begin{tikzpicture}[scale=1.0545]\small \tikzset{>=stealth} \def\k{50} \def\p{3.1415926/\k} \def\r{3.1} \def\l{5.8} \def\t{0.07} \draw[->,thin,gray] (-\l,0)--(\l,0); \draw[->,thin,gray] (0,-0.6)--(0,\l); \draw[green!40!black](\r,0) -- (\r,\p*\r) node[midway,right] {$i\pi/\k$}; \foreach \l in {1,...,\k} \draw[->] (0,0) -- ({(\l-1)*atan(\p)}:{((sqrt(1+\p*\p)^(\l-1)*\r)}); \draw[->,red] (0,0) -- ({\k*atan(\p)}:{((sqrt(1+\p*\p)^\k*\r)}); \draw[very thin] (\r,\t)--(\r,-\t) node[below]{$1$} (-\r,\t)--(-\r,-\t) node[below]{$-1$} (\t,\r)--(-\t,\r) node[left]{$1$} (0,0) node [anchor=north west,yshift=-0.07cm] {$0$}; \draw [line width=0.2mm,opacity=0] (-\l,-0.6) rectangle (\l,\l); \end{tikzpicture}$$
URL последней картинки длиной 1192 символа. В принципе, такие длинные адреса не очень красивы. Но и большой проблемы в этом нет. В стандарте нет ограничений на длину URL, да и с практическим ограничением в браузере или
Меня просили изменить алгоритм кодирования, чтобы укоротить адреса.
Необходимости в этом я пока не вижу. Но если буду делать доработку, то поступлю аналогично. Адрес /svgb/... с закодированными в /gb/... на дешифрованный вариант в редакторе формул.
Объемный чертеж
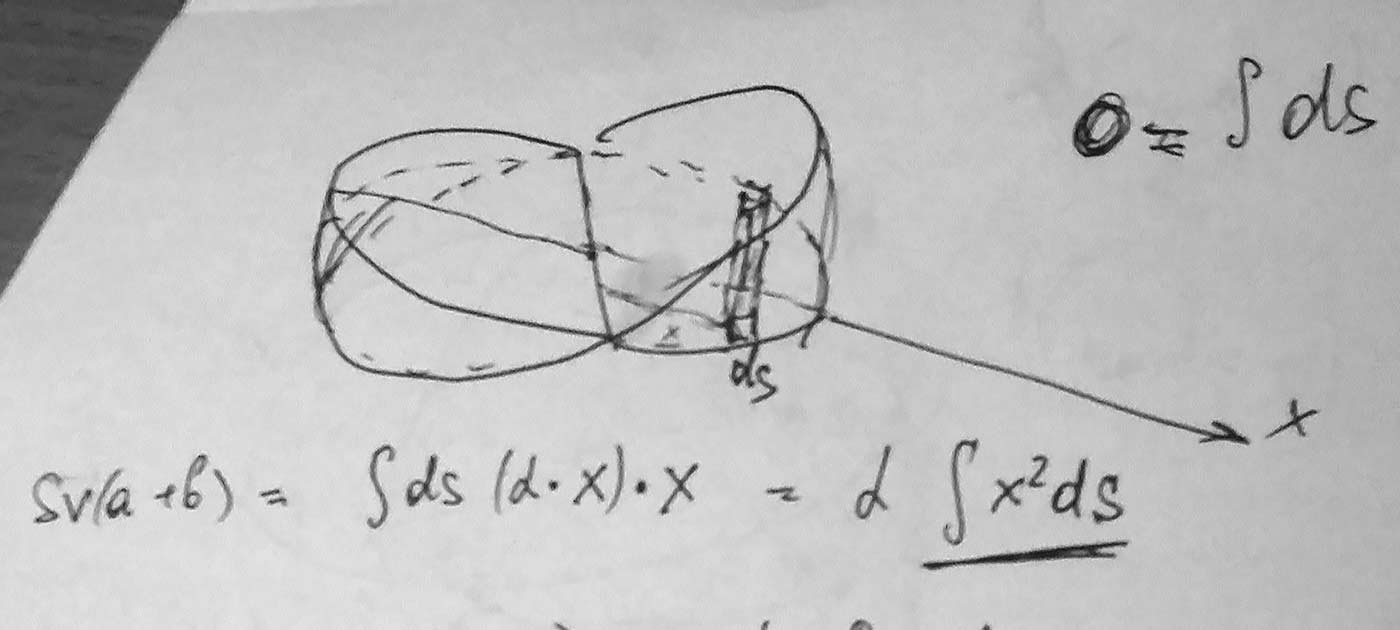
Нарисовал в латехе объемный чертеж, но он не пригодился. Так что просто оставлю его здесь.
Чтобы делать такие чертежи, добавил в свой редактор математических текстов Upmath поддержку пакета
Сравните с версий того же чертежа из черновика:
Синхронная прокрутка
Этот текст я написал в том числе и для себя, чтобы в следующий раз не попадать в ловушку «почему два года назад я сделал так криво, сейчас всё исправлю».
Иногда в интерфейсе нужно одновременно показать два документа с синхронной прокруткой. Прокручиваешь левый документ, и правый тоже прокручивается до соответствующего места. И наоборот. Может показаться, что задача синхронной прокрутки не слишком сложная. Но на самом деле это не так.
Пример синхронной прокрутки есть в каждом интерфейсе просмотра изменений файлов. Вот PhpStorm:
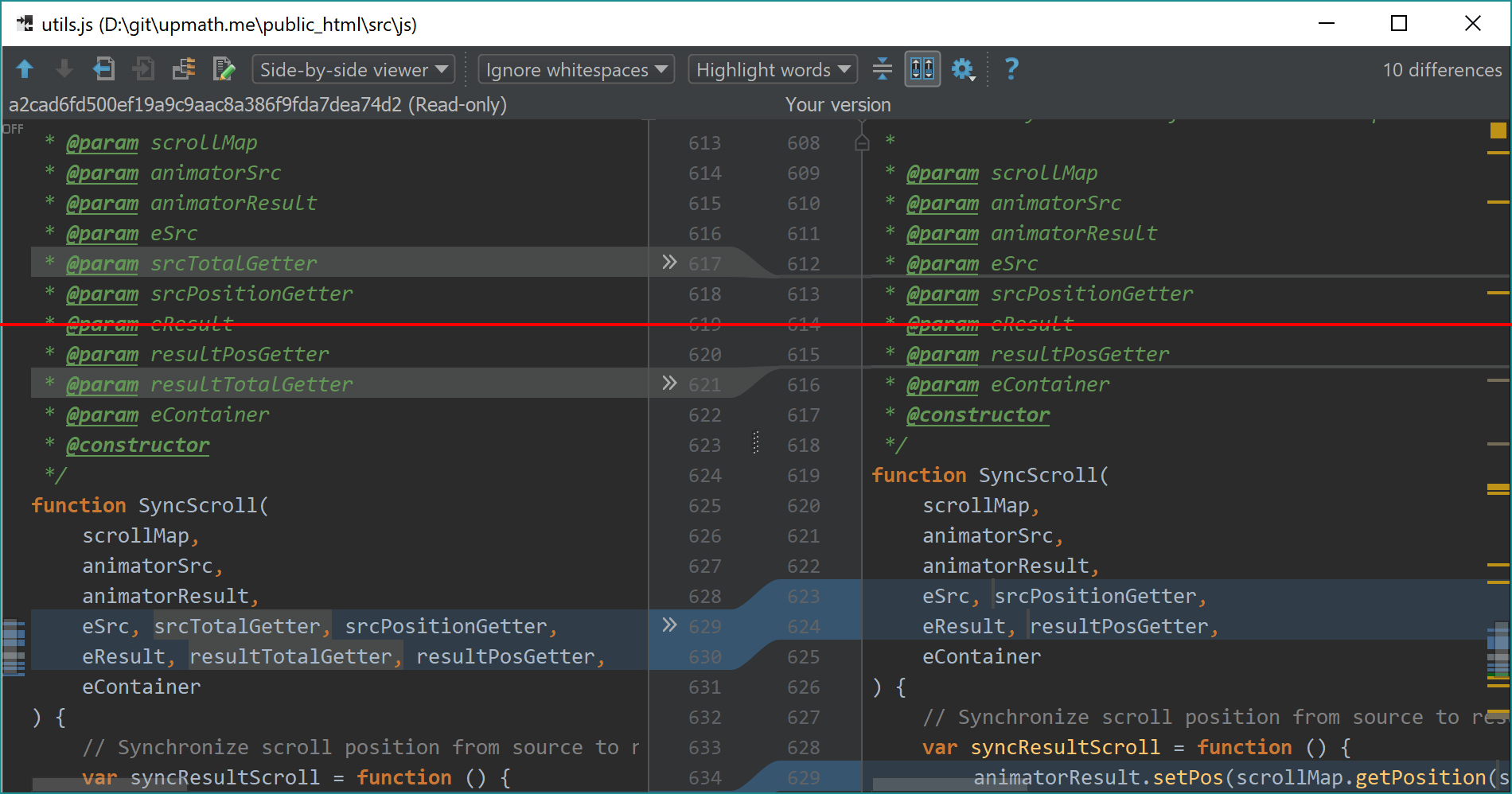
При прокрутке одной версии документа вторая всегда выравнивается так, чтобы на красной линии оказались соответствующие строки. Аналогичный способ я выбрал для своего редактора математических текстов, только ориентир выравнивания сделал посередине:
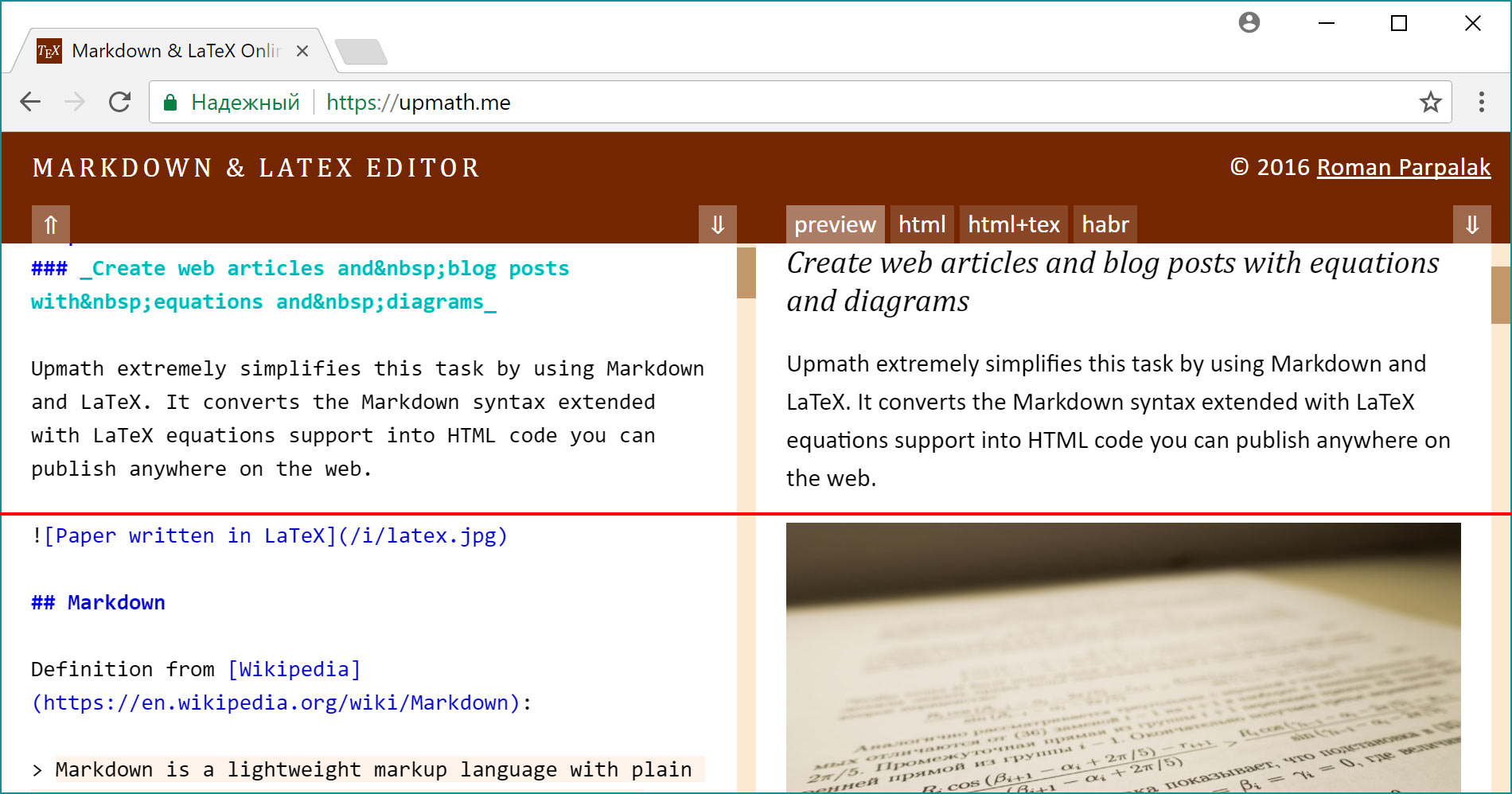
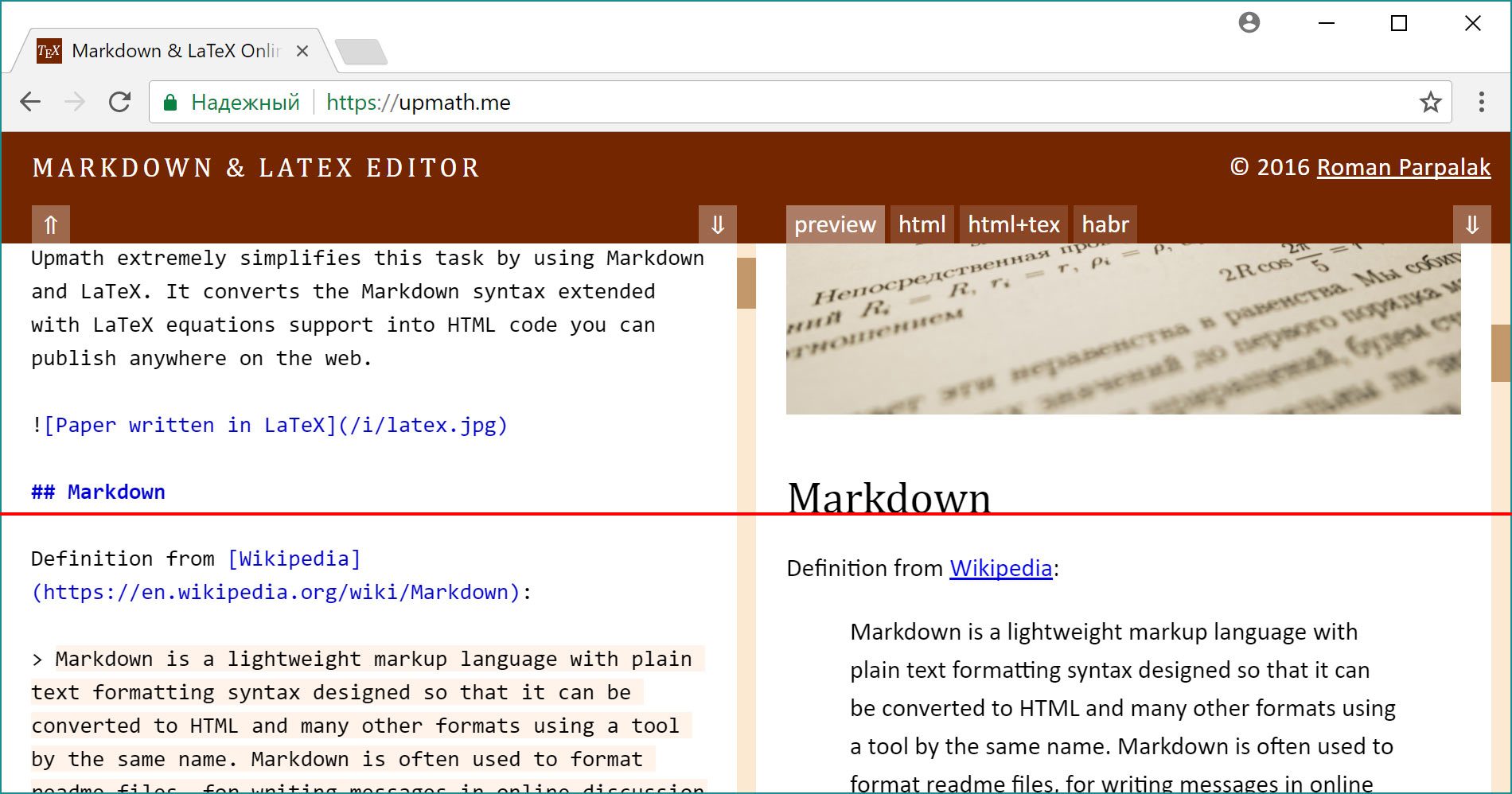
Здесь мы набираем исходный код и сразу же видим результат. Обратите внимание на неравномерность прокрутки. Слева картинка кодируется одной строкой, а справа она занимает почти всю высоту прокручиваемой области.
Такая неравномерность приводит к ряду проблем. Когда картинка добавляется последней строчкой, в предпросмотре отображается только ее верхушка:
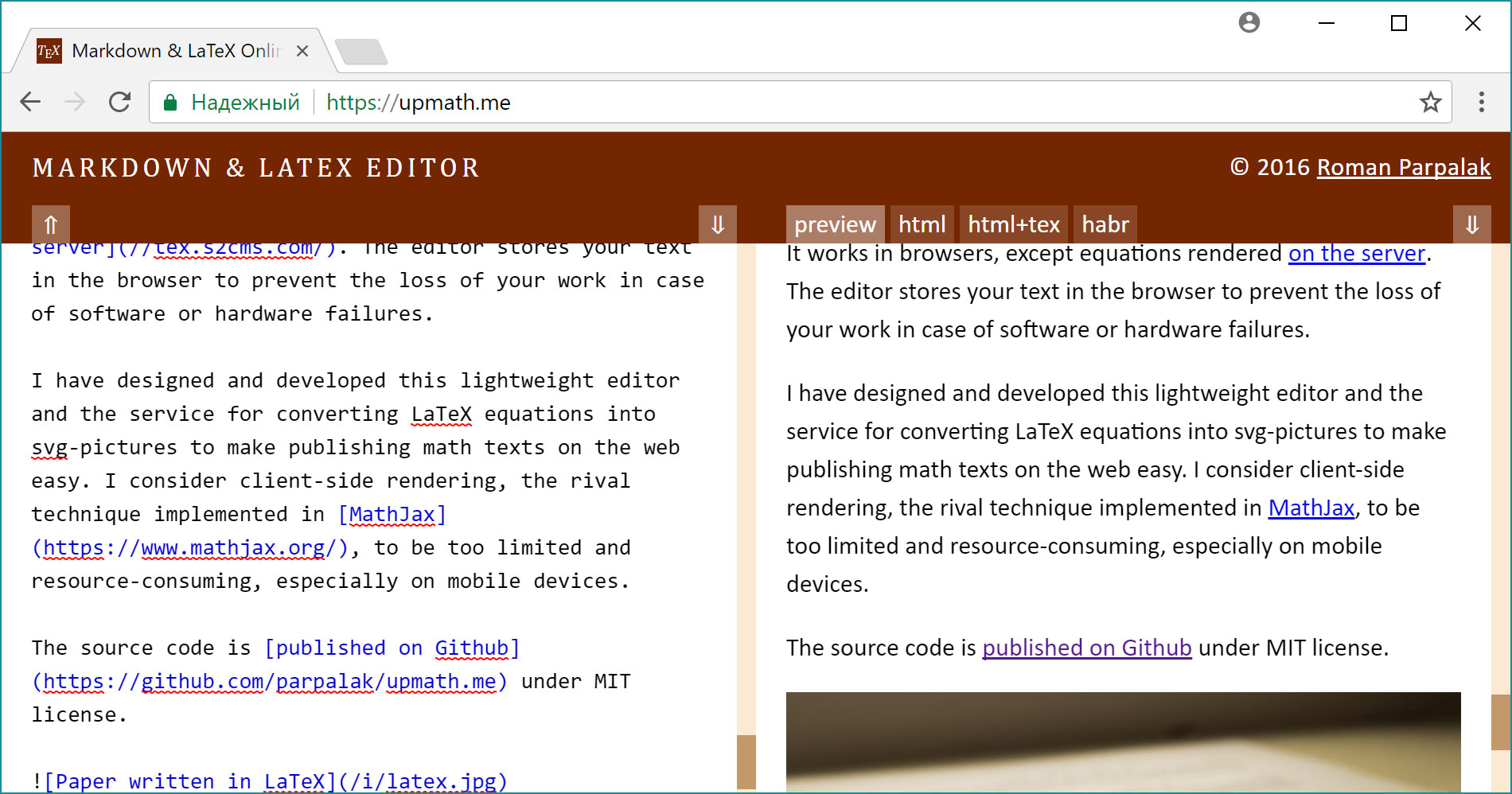
Это естественное поведение алгоритма с выравниванием по ориентиру в центре. И его хотелось бы улучшить. Но от
Другая идея — сделать ориентир не фиксированным, а подвижным. Сначала ориентир расположен вверху. Затем, по мере прокрутки, он сдвигается вниз. Но и здесь нас ждут скользкие моменты. Например, мы знаем, что начало одного и того же абзаца находится в левом документе на высоте в 30%, а в правом на 50%. Пусть левый документ прокрутили на 30%. Тогда мы говорим, что ориентир тоже находится на 30% высоты экрана, переводим 30% в 50%, и располагаем правый документ так, чтобы абзац был на 30% высоты экрана. Проблема в том, что обратное преобразование не обязано давать тот же самый результат. Действительно, тот же самый абзац будет использоваться при прокрутке правого документа на 50%, и в общем случае это разные положения прокрутки. В такой реализации встречаются странные скачки прокрутки при переключении фокуса между документами и даже немонотонность зависимой прокрутки: если вы прокручиваете один документ вниз, то другой в некоторые моменты будет двигаться не вниз, а вверх.
У меня была мысль отказаться от двух прокручиваемых областей, прокручивать только исходный код и умным алгоритмом выводить в области предпросмотра соответствующую область документа. Но проблемы синхронной прокрутки, о которых я рассказал, мешают это сделать.
Похоже, полностью избавиться от проблем синхронной прокрутки вообще нельзя. Вернемся к сравнению файлов. Предположим, в одном файле 100 строк, во втором я превратил сотую строку в еще 400. Прокручивая первый файл, мы никогда не увидим новые 400 строк второго. Как бы мы ни выравнивали второй файл, все 400 строк на экран не поместятся. Это значит, что нельзя убирать вторую прокрутку.
В своем редакторе я оставил синхронизацию прокрутки по ориентиру, но дополнил ее условием: если один документ полностью прокручен вверх или вниз, то второй документ прокручивается полностью.
Естественная анимация в интерфейсах
Анимация в интерфейсе делает наглядным изменение его состояния. Например, при неудачной отправке длинная форма прокручивается к неправильно заполненному полю. Или увеличивающаяся по нажатию фотография раздвигает окружающие элементы.
Без анимации сложнее воспринимать резкие и внезапные изменения. Вместе с тем анимация должна быть короткой и ненавязчивой, чтобы не мешать пользователю.
Анимация кажется естественной, когда повторяет привычное движение предметов окружающего мира. Я расскажу, как делал анимацию в своем редакторе математических текстов Upmath на основе физических законов. Готовый результат в изолированном окружении смотрите на
Вспоминаем физику
Перемещение объектов описывается изменением координат x с течением времени t. Если вы попытаетесь подобрать функцию x(t) «на глазок», потратите много времени, добиваясь плавного и естественного движения. Что выбрать? Гиперболу? Параболу? Куда ее переместить? Как повернуть?
За примерами движения лучше всего обратиться к предметам окружающего мира. Математический закон их движения диктуется физикой. Толкнем брусок, лежащий на столе. Он проходит определенное расстояние, замедляясь под действием силы трения. В хорошем приближении сила сухого трения скольжения постоянна, и зависимость x(t) оказывается параболой. Такое замедление можно использовать, если в начальный момент объект анимации уже двигался.
$$\begin{tikzpicture} \def\t{0} \def\r{3.4} \begin{axis}[width=10cm,height=7cm, ticks=none, xmin=-0, xmax=3.8, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true,mark size=1 ] \addplot[smooth,blue,domain=\t:\r,samples=80]{-(x-\r)^2} node[pos=0.75,black,anchor=south east,inner sep=2pt]{$x=A+Bt+Ct^2$}; \addplot[dashed,domain=\r-0.7:\r,samples=2]{0}; \addplot[mark=*] coordinates {(\t,-\r*\r)}; \addplot[mark=*,green!50!black] coordinates {(\r,0)} node[pin=-90:{\footnotesize{\text{\sffamily плавная остановка :)}}}]{}; \end{axis} \end{tikzpicture}$$
Рис. 1. Торможение сухим трением по параболе
Сила вязкого трения пропорциональна скорости движения тела. В таком случае тело будет двигаться к точке остановки по экспоненте за бесконечно большое время. Если экспоненту исказить, чтобы ограничить время движения, такая анимация будет казаться неестественной.
$$\begin{tikzpicture} \def\t{0} \def\r{3.8} \begin{axis}[width=10cm,height=7cm, ticks=none, xmin=-0, xmax=3.8, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true,mark size=1 ] \addplot[smooth,blue,domain=\t:\r,samples=80] {1-exp(-x*1.0)} node[pos=0.45,black,anchor=south east,inner sep=2pt]{$x=A-Be^{-\alpha t}$}; \addplot[dashed,domain=\t:\r,samples=2]{1}; \addplot[mark=*] coordinates {(\t,0)}; \addplot[red!80!black] coordinates {(3.4,1)} node[pin=-90:{\footnotesize{\text{\sffamily не останавливается :(}}}]{} ; \end{axis} \end{tikzpicture}$$
Рис. 2. Торможение по экспоненте в вязкой среде
Отклоненный от положения равновесия маятник (или грузик на пружине) плавно набирает скорость, проходит положение равновесия и плавно тормозит. Затем движение повторяется в обратную сторону, и так до бесконечности (если трения нет). График такого движения — синусоида. Периодический повтор нам не особо интересен, а вот движение маятника между крайними точками получается плавным и естественным.
$$\begin{tikzpicture} \def\t{0} \def\r{3.1415} \begin{axis}[width=10cm,height=7cm, ticks=none,mark size=1, xmin=-0.5, xmax=3.6, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true ] \addplot[smooth,blue,domain=\t:\r,samples=80] {1-cos(deg(x))} node[pos=0.52,black,anchor=south east,inner sep=2pt]{$x=A-B\cos\omega t$}; \addplot[dashed,domain=\t:\t+0.6,samples=2] {1-cos(deg(\t))}; \addplot[dashed,domain=\r-0.6:\r,samples=2] {1-cos(deg(\r))}; \addplot[mark=*,green!50!black] coordinates {(\t,0)} node[pin=90:{\footnotesize{\text{\sffamily плавный запуск :)}}}]{}; \addplot[mark=*,green!50!black] coordinates {(\r,2)} node[pin=-90:{\footnotesize{\text{\sffamily\quad плавная остановка :)}}}]{}; \end{axis} \end{tikzpicture}$$
Рис. 3. Движение маятника по синусоиде между крайними точками
В
- Синусоидальная траектория переводит тело из одного покоящегося положения в другое.
- Продолжительность такого движения ограничена по времени и равна половине периода. То есть эта продолжительность зависит не от внешних обстоятельств и начальных условий, а только от свойств самой системы, и определяется соотношением жесткости и инерционности.
Обычно я выбираю длительность анимации по синусоиде в 200 миллисекунд. Такая длительность в несколько раз больше времени реакции человека. Анимация хорошо заметна, но не успевает раздражать.
Давайте научимся проводить синусоидальную траекторию по начальным условиям, времени движения и точке остановки.
Как провести синусоиду через две точки
Пусть тело покоится в начальный и конечный момент времени. Тогда касательные к графику в точках t1 и t2 горизонтальны, а сам график — это полупериод синусоиды.
$$\begin{tikzpicture} \def\t{0} \def\r{3.1415} \begin{axis}[ ticks=none, xmin=-1, xmax=4.5, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true ] \addplot[smooth,blue,domain=\t:\r,samples=80] {1-cos(deg(x))}; \addplot[dashed,domain=\t:\t+1,samples=2] {1-cos(deg(\t))}; \addplot[dashed,domain=\r-1:\r,samples=2] {1-cos(deg(\r))}; \addplot[mark=*,mark size=1] coordinates {(\t,0)} node[pin=95:{$(t_1,x_1)$}]{} ; \addplot[mark=*,mark size=1] coordinates {(\r,2)} node[pin=-85:{$(t_2,x_2)$}]{} ; \end{axis} \end{tikzpicture}$$
Рис. 4. График движения между двумя положениями покоя
Уравнение, описывающее полупериод синусоиды, легко подобрать:
$$x(t)=x_1+{x_2-x_1\over 2}\left[1 - \cos\left(\pi{t-t_1\over t_2-t_1}\right)\right].$$
После окончания одной анимации мы можем начинать другую опять по этой формуле. Но что делать, если новая анимация должна начаться, пока еще не закончилась старая? Чтобы обеспечить плавность движения, мы останавливаем текущую анимацию (синяя линия) и начинаем новую анимацию (красная линия) с ненулевой начальной скоростью:
$$\begin{tikzpicture} \def\tgnt{0.7} \def\t{0} \def\r{3.1415} \def\tb{1} \def\rb{\r+\tb} \def\dx{1.27} \begin{axis}[ ticks=none, xmin=-1, xmax=4.9, axis y line=left,axis x line=bottom, xlabel=$t$,ylabel=$x$, every axis x label/.style={at={(current axis.south east)},anchor=south}, every axis y label/.style={at={(current axis.north west)},anchor=west}, enlargelimits=true,mark size=1 ] \addplot[smooth,blue,domain=\t:\tb,samples=80] {-cos(deg(x))+1}; \addplot[smooth,dotted,blue,domain=\tb:\r,samples=10] {-cos(deg(x))+1}; \addplot[blue,dashed, domain=\t:\t+\tgnt,samples=2] {-cos(deg(\t))+1}; \addplot[smooth,thick,red,domain=\tb:\rb,samples=80] {-1.5*cos(deg(1+0.69*(x-\tb)))+\dx}; \addplot[dashed,red,domain=\tb-\tgnt:\tb+\tgnt,samples=2] {-1.5*cos(deg(\tb))+\dx+sin(deg(\tb))*(x-\tb)}; \addplot[dashed,red,domain=\rb-\tgnt:\rb,samples=2] {1.5+\dx}; \addplot[mark=*] coordinates {(\t,0)}; \addplot[mark=*] coordinates {(\tb,1-cos(deg(\tb)))} node[pin=-85:{$(t_1,x_1)$}]{} ; \addplot[mark=*] coordinates {(\r,2)}; \addplot[mark=*] coordinates {(\rb,1.5+\dx)} node[pin=-85:{$(t_2,x_2)$}]{} ; \end{axis} \end{tikzpicture}$$
Рис. 5. График движения с ненулевой начальной скоростью
Без математических вычислений не получится написать формулу, соответствующую красной линии. Давайте проделаем эти вычисления.
Семейство всех возможных синусоид описывается уравнением
$$f(t)=A\cos\omega (t-t_2)+B\sin\omega (t-t_2)+C$$(1)
с четырьмя неизвестными параметрами A, B, C и $$\omega>0$$. Я сдвинул начало отчета времени в точку t2, чтобы сразу избавиться от второго слагаемого. Действительно, производная $$f'(t_2)=B\omega$$ должна быть нулевой, потому что касательная в точке t2 горизонтальна. Это возможно, когда B=0.
Так как $$f(t_2)=x_2$$, то подставляя $$t=t_2$$ в (1), получаем $$f(t_2)=A+C$$. Отсюда исключаем C:
$$f(t)=x_2 + A\left[\cos\omega (t-t_2)-1\right].$$
Продифференцируем, чтобы найти скорость
$$f'(t)=-A\,\omega\sin\omega (t-t_2).$$
Нам известно положение x1 и скорость v в начальный момент времени:
$$\begin{cases} x_1\!\!\!\!\!&=x_2+A\left[\cos\omega(t_1-t_2)-1\right],\\ v\!\!\!\!\!&=-A\,\omega\sin\omega(t_1-t_2). \end{cases}$$
Из этой системы уравнений нужно найти A и $$\omega$$. Пора вводить новую переменную $$k=\omega(t_2-t_1)$$ вместо $$\omega$$. Ее смысл — разность фаз синусоиды в начальной и конечной точке. Например, для графика на рис. 4 $$k=\pi$$, потому что на промежутке $$(t_1,t_2)$$ укладывается полупериод синусоиды. На рис. 5 $$k<\pi$$, потому что $$t_2-t_1$$ меньше половины периода.
После подстановки и небольших преобразований приходим к системе
$$\begin{cases} x_2-x_1&=A\left(1-\cos k\right),\\ v(t_2-t_1)\!\!\!\!&=A\,k\sin k. \end{cases}$$
Разделим почленно первое уравнение на второе:
$${x_2-x_1\over v(t_2-t_1)}={1-\cos k\over k\sin k}\quad \Rightarrow\quad{1-\cos k\over\sin k}=\alpha k,\quad\text{где} \ \alpha={x_2-x_1\over v(t_2-t_1)}.$$
Параметр $$\alpha$$ в правой части известен заранее. Он определяет требуемый характер движения. Если $$\alpha\gg1$$, то начальная скорость мала, тело сначала должно ускориться. Если $$\alpha\ll1$$, начальная скорость велика, тело должно замедляться.
Тригонометрические функции в левой части сводятся к тангенсу половинного угла. В итоге у нас нелинейное уравнение относительно k:
$$\text{tg}\,{k\over2}=\alpha k.$$(2)
Проанализировать его решения можно на графике. Нарисуем график левой и правой части при некоторых значениях параметра $$\alpha$$:
$$\begin{tikzpicture}\small \def\aa{1.5} \def\ab{0.3} \def\ac{-0.5} \begin{axis}[legend pos=south east,mark size=1,samples=2, restrict y to domain=-8:8, width=12cm, height=250pt, xmin=-10.5, xmax=10.5, ytick={-6,-3,...,6}, xtick={-9.4247,-3.1416,...,10}, xticklabels={$-{3\pi}$,$-{\pi}$,${\pi}$,${3\pi}$}, axis x line=center, axis y line=center, xlabel=$k$] \addplot[blue!70!black,domain=-9.4247:9.4247,semithick,samples=802]{tan(deg(x/2))}; \addplot[red]{\aa*x}; \addplot[green!70!black,domain=-9.4247:9.4247]{\ab*x}; \addplot[olive,domain=-9.4247:9.4247]{\ac*x}; \addplot[mark=*] coordinates {(2.65,3.97)} node[anchor=west,inner sep=2pt]{$A$}; \addplot[mark=*] coordinates {(8.69,2.61)} node[anchor=west,inner sep=1pt,yshift=-4pt]{$B$}; \addplot[mark=*] coordinates {(4.06,-2.03)} node[anchor=west,yshift=2]{$C$}; \legend{$y=\tg k/2$,$y=\aa\,k$,$y=\ab\,k$,$y=\ac\,k$} \end{axis} \end{tikzpicture}$$
Рис. 6. Графическое решение уравнения (2)
Обсудим получившиеся решения.
-
Рассмотрим точку A. Это решение существует при $$\alpha>1/2$$ и соответствует изображенному на рисунке 5: $$\begin{tikzpicture} \def\t{1} \def\r{3.1415} \begin{axis}[width=1.9cm,height=2cm,hide axis,ticks=none, xmin=\t,xmax=\r,mark size=0.3] \addplot[smooth,blue,domain=\t:\r,samples=80] {-cos(deg(x))}; \addplot[mark=*] coordinates {(\t,-cos(deg(x)))}; \addplot[mark=*] coordinates {(\r,-cos(deg(x)))}; \end{axis} \end{tikzpicture}$$. Как ожидалось, $$k<\pi$$. В пределе нулевой скорости $$\alpha\to\infty$$, красная прямая совпадет с осью ординат, точка A уйдет по тангенсоиде в бесконечность. В этом пределе $$k\to\pi$$. Пока всё идет правильно.
-
Точка C отвечает значению $$\alpha<0$$. Такое случается, когда тело в первый момент времени движется вперед, а надо двигаться назад. Теперь $$\pi<k<2\pi$$. Движение описывается фрагментом синусоиды, большим чем полупериод, но меньшим, чем период: $$\begin{tikzpicture} \def\t{-1.7} \def\r{3.1415} \begin{axis}[width=2.2cm,height=2cm,hide axis,ticks=none, xmin=\t,xmax=\r,mark size=0.3] \addplot[smooth,blue,domain=\t:\r,samples=80] {cos(deg(x))}; \addplot[mark=*] coordinates {(\t,cos(deg(x)))}; \addplot[mark=*] coordinates {(\r,cos(deg(x)))}; \end{axis} \end{tikzpicture}$$. Тело тормозит, останавливается, движется назад и останавливается в требуемом месте.
-
Из графика видно, что при $$0<\alpha<1/2$$ точка B попадает в диапазон $$2\pi<k<3\pi$$. Тело пройдет по синусоиде больше, чем полный период колебаний: $$\begin{tikzpicture} \def\t{-1.6} \def\r{2*3.1415} \begin{axis}[width=2.5cm,height=2cm,hide axis,ticks=none, xmin=\t,xmax=\r,mark size=0.3] \addplot[smooth,blue,domain=\t:\r,samples=80] {cos(deg(x))}; \addplot[mark=*] coordinates {(\t,cos(deg(x)))}; \addplot[mark=*] coordinates {(\r,cos(deg(x)))}; \end{axis} \end{tikzpicture}$$. Причина такого странного решения в том, что точка остановки находится слишком близко по сравнению с характерным расстоянием
v (t2 − t1) . Поэтому провести синусоиду без дополнительной остановки и возврата не получится.
Небольшое лирическое отступление: похожие на (2) уравнения возникают при решении задач квантовой механики про уровни энергии частиц в прямоугольных потенциальных ямах. Там приходится сшивать, например, синусоиду и экспоненту. Условие отсутствия изломов дает подобные уравнения с бесконечным количеством корней.
Приближенное решение
Мы решили математическую задачу проведения синусоиды, но жизнь от этого проще не стала.
Эти трудности возникли от того, что мы зафиксировали продолжительность анимации ровно в 200 миллисекунд. Однако ничего страшного не случится, если анимация продлится, скажем, 180 миллисекунд. Или даже 250 миллисекунд. Нам важнее остановка в заданном месте, а точной продолжительностью анимации мы пожертвуем для упрощения расчетов.
Ослабив требования на продолжительность анимации, мы проделаем такой трюк. Предположим, что у нас есть приближенное решение $$k'$$ нелинейного уравнения (2). Оно является точным решением уравнения с другим параметром
$$\alpha'={1\over k'}\,\text{tg}{k'\over 2},$$
Ему соответствует другое время окончания анимации:
$$t_2'=t_1+{x_2-x_1\over v\alpha'}.$$
Теперь неизвестные параметры траектории A и $$\omega$$ элементарно выражаются через $$k'$$ и $$\alpha'$$.
Я подобрал подходящее для наших целей приближение к уравнению (2):
$${1\over 2\alpha}\approx1-\left({k\over\pi}\right)^2.$$
Синяя сплошная линия соответствует точному уравнению (2), а красная пунктирная — его приближению:
$$\begin{tikzpicture}\small \begin{axis}[legend pos=south east, restrict y to domain=-8:8, width=12cm, xmin=-7.3, xmax=7.3, ytick={-6,-3,...,6}, xtick={-6.2832,-3.1416,...,10}, xticklabels={$-{2\pi}$,$-{\pi}$,$0$,${\pi}$,${2\pi}$}, axis x line=center,axis y line=center, xlabel=$k$,ylabel=$\alpha$] \addplot[smooth,samples=580,blue!70!black,domain=-7:7]{tan(deg(x/2))/x}; \addplot[smooth,samples=580,red,dashed,domain=-7:7]{0.5/(1 - (x/pi)^2)}; \legend{$(1/k)\,\text{tg}\,k/2$,$0.5/\!\left[1 - ({k/\pi})^2\right]$} \end{axis} \end{tikzpicture}$$
Рис. 7. Сравнение точного соотношения (2) и его приближения
А еще в случае $$0<\alpha<1/2$$ предлагаю взять $$\alpha'$$ чуть больше, чем 1/2, и сократить время анимации, чтобы избежать отскока и возврата.
Применение
Код и пример использования есть на
Описанную схему я разработал для синхронной прокрутки исходного кода и предпросмотра в своем редакторе математических текстов Upmath.
Идею и первоначальную реализацию нашел на
- Для анимации применяется линейная функция:
$(...).stop(true).animate( {scrollTop: ...}, 100, 'linear' ). Вместо гладкого графика получается ломаная. - Анимация через
jQuery().stop().animate()тормозит по сравнению сrequestAnimationFrame(). - Чтобы избежать падения производительности, «проглатываются» события
onscroll, следующие чаще чем 50 миллисекунд. В моем варианте такой проблемы нет. Последовательные событияonscrollкорректируют положение точки остановки и не замедляют анимацию.
Чтобы добиться важной для продукта качественной анимации, я проработал метод вычисления на основе физических уравнений, и реализовал его через специальный браузерный метод requestAnimationFrame(). Метод хорошо работает при любой прокрутке: клавишами PageUp/PageDown, через перемещение полос прокрутки, колесико мыши, тачпад, тачскрин.
Статья впервые опубликована на хабре.
Формулы
Открываем 10 лучших публикаций на хабре за неделю и видим, что на четвертом месте статья «Сказ царя Салтана о потенциале лапласиана», на пятом — «Байесовская нейронная сеть — теперь апельсиновая (часть 2)». И обе с использованием моего сервиса для формул.
Неплохо, я считаю :)
См. Markdown and LaTeX online editor и описание на хабре.
Латех в вебе
Постоянные читатели помнят, что у меня есть движок сайтов S2, и он с помощью расширения s2_latex ищет в тексте страницы формулы на латехе и заменяет их на картинки. Расширение обращается к сервису codecogs.com. Этот сервис зачастую глючит, и я уже давно сделал свой, с
Мой сервис делает из формул картинки. Вот, для примера, знакомое всем решение квадратного уравнения в SVG и PNG:
На обычных мониторах преимуществ у SVG нет. Но на ретине или при большом увеличении SVG выглядит более чем достойно. А за ретиной будущее.
В
Символы в формулах крупнее и жирнее, чем в окружающем тексте. Они в буквальном смысле выпадают из окружающего текста. Меняем гротеск на антикву, увеличиваем кегль и добавляем выравнивание по базовой линии:
Теперь буквы в формулах аккуратно располагаются на тех же линиях, что и буквы в окружающем тексте. Чтобы заработала магия с выравниванием по базовой линии, к странице нужно подключить специальный скрипт.
У
Я подготовил описание сервиса и инструкцию. Посмотреть сервис в работе можно в блоге о теоретической физике. В следующий раз я расскажу о том, как всё это работает.