Савватеев и Шпилькин разбирают статистику с выборов

Сергей Шпилькин — это тот самый физик, который обрабатывает математическими методами данные с выборов. Если вы до сих пор не читали и не разбирались в его результатах, посмотрите, как они с Савватеевым обсуждают графики, гипотезы и вообще применимость к выборам математических методов как таковых.

Пару раз они забылись и произнесли понятные только специалистам термины вроде «минимального детерминанта матрицы ковариации», но на восприятии основного посыла это не сказалось.

Переезд сайта на parpalak.com

На выходных перевел этот сайт с домена written.ru на parpalak.com. Я затеял этот переезд не только из-за красоты домена, которая не особо-то и нужна в современном интернете победивших соцсетей, а скорее из-за изменений в российском интернете.

---

Домен второго уровня я решил зарегистрировать в 2006 году. Рассматривал разные варианты. Домен parpalak.ru оказался занятым. По данным whois его зарегистрировал некий Орест Парпалак. Никакого сайта на этом домене не было, домен использовался для почты. Домен roma.ru тоже оказался занятым. Сейчас по нему открывается сообщение, что домен не продается. А вот раньше там была даже фотография, возможно того самого Ромы.

В итоге я зарегистрировал written.ru. Идею взял у Ромы Воронежского с его сайтами narisoval.ru и napisal.ru, просто перевел слово «написал» на английский.

В 2017 году я обнаружил, что домен parpalak.ru освободился, и зарегистрировал его. Через некоторое время зарегистрировал и parpalak.com, на случай если захочу сделать англоязычный сайт. Кстати, с последним доменом произошла интересная история. Я прописал у регистратора ns-серверы своего хостинга (ns1.linode.com), а в хостинге домен не добавил. Какой-то хитрый пользователь этого хостинга обнаружил это и добавил домен parpalak.com к себе. После чего у меня уже не получилось его добавить. К счастью, никакого контента на сайте по A-записям не оказалось. Я написал в поддержку и проблема была сразу же решена.

---

И вот наступил 2021 год. Государство на полном серьезе принялось «регулировать» интернет (на хабре недавно вышел обзор изменений за последние полгода). Я решил, что пора заняться вопросом информационной безопасности. Не то чтобы я ощутил какую-либо угрозу здесь и сейчас. Но и игнорировать политическую обстановку и произвол силовиков тоже нельзя. Составил контрольный список:

• хостинг — в Европе, ничего делать не надо;
• почта — яндексовская, есть риск взлома или потери;
• домены у российских регистраторов — есть риск отключения или потери.

Я решил оставить российские домены у российских регистраторов и принять соответствующие риски. Остальные домены перенес к регистратору NameSilo. Ссылка реферальная: если решите воспользоваться рекомендацией, получу немного денег. Вроде бы у них самые дешевые домены: домен .com чуть дешевле 10 долларов. Кроме покупки можно переносить имеющиеся домены. Для переноса нужно получить у текущего регистратора код авторизации (примерно так же я переносил домены от Ру-центра к Бегету). Причем NameSilo позаботился, чтобы клиенты из-за переноса ничего не теряли: сам перенос стоит чуть дешевле годовой стоимости домена, а к текущему сроку регистрации добавляется год.

В итоге я перенес от российских регистраторов домены редактора математических текстов Upmath, головоломки Арнольда и s2cms.com. Для черновиков физика зарегистрировал новый домен susy.page вместо susy.written.ru. Киноблог и сайт программы с игрой «Жизнь» остались на своих доменах kinoblog.su и life.written.ru, мне их не жалко.

Последним шагом, как и написал в самом начале, сделал основным доменом parpalak.com вместо written.ru. Этим шагом решается и проблема почты. Дело в том, что почтовым сервисом для written.ru я настроил в 2010 году яндексовскую почту для домена, которая перенаправляет все входящие на гугловскую почту. С этим я ничего делать не буду. Просто сделаю основным почтовый ящик на другом домене.

---

После переезда обнаружилась только одна небольшая проблема — feedly заново показал последние посты. Скорее всего из-за изменения УРЛов, так как они использовались как идентификаторы записей:

<guid isPermaLink="true">https://parpalak.com/blog/2021/09/12/smart_vote</guid>

При этом feedly проигнорировал поле pubDate и показал записи как свежие. Можно было избежать этой проблемы, если специально для RSS запоминать адреса записей. Но я не думаю, что хоть кто-либо когда-либо озаботился и запрограммировал такую фичу.

Умное голосование как второй тур

Умное голосование — это как второй тур на выборах без второго тура. Давайте переквалифицируемся из вирусологов и востоковедов опять в политологи и порассуждаем на эту тему.

Голосование на выборах бывает устроено множеством разных способов: в один тур часто выбирают парламенты, в два тура — президентов. В Америке президента вообще избирают промежуточные выборщики.

Голосование через неделю, 19 сентября, будет происходить по смешанной системе: половина мест в парламенте распределяется между партийными списками, половина мест — по одномандатным округам. Каждый избиратель голосует за одну из партий по общему (федеральному) списку и за одного из кандидатов по местному округу.

Стратегия голосования по федеральному списку для тех, кому надоела несменяемость власти, не изменилась: голосуй за любую партию кроме партии жуликов и воров. При следовании этой стратегии количество мест у жуликов и воров будет снижаться.

Стратегия голосования по одномандатному списку не так очевидна. Место в Думе получает кандидат, набравший наибольшее число голосов. При этом второго тура нет: даже если единорос набрал 20%, а 80% размазались по остальным кандидатам, в Думу пройдет единорос. Задача умного голосования — исключить размазывание голосов по кучке кандидатов. Если бы голосование по одномандатным округам проходило в два тура, то в первом туре можно было бы голосовать за понравившегося кандидата, а во втором туре — за наименее противного. К сожалению, второго тура нет, поэтому приходится изобретать костыли вроде умного голосования.

Оппоненты умного голосования утверждают, что в других партиях люди не сильно лучше, и даже если Единая Россия не получит большинства в думе, мы вряд ли проснемся следующий день в другой стране. Нас убеждают, что нельзя голосовать за коммунистов, сталинистов, националистов и прочих «истов». Какой тогда смысл голосовать за кого-либо?

Смысл голосования в нынешних условиях в том, что процент голосов за Единую Россию — неплохой показатель общественного мнения (сфальсифицированные голоса, как обычно, отфильтруют методом анализа данных). А партии-сателлиты в парламенте могут обрести самостоятельность в случае раскола элит, перспектива которого может приблизиться при низком результате Единой России.

Логотип Медузы и энергия

Интервью с Григорием Кравченко, автором логотипа Медузы. Извините, не могу не процитировать:

«Медуза» делалась с колоссальной энергией. Тебе сузили пространство, ты весь напрягся, и эта кинетическая энергия должна распрямиться и на максимуме сделать что-то очень быстрое, агрессивное. Это злость, но она в итоге позитивная, не вредная. Тебе нужно отреагировать, у тебя что-то отобрали — и ты хочешь сделать новое.

Тут всё хорошо, но когда сужают пространство и ты напрягаешься, накапливается потенциальная энергия, а не кинетическая.

Поиграл на рояле в аэропорту

Как просили в прошлый раз в комментариях, снял на видео, как поиграл в аэропорту. Не без ошибок, потому что клавиатура непривычная: черные клавиши оказались слишком тонкие. Да и месяц не садился за инструмент. Вот несколько фрагментов:

0:00 Разминка
1:20 Chilly Gonzales — Dot
1:51 Roman Parpalak — Ursa Minor
3:39 Ludovico Einaudi — Nightbook
5:22 Chilly Gonzales — Gogol
6:25 Secret Garden — Song from a Secret Garden

Фейковый pop3-сервер

Я оказался в ситуации почти без доступа к некоторому почтовому ящику. Пароль не помнил, но этот пароль был сохранен в почтовом клиенте The Bat. Почтовик вроде как защищает пароль: его нет в открытом виде в конфиге и его нельзя скопировать из окна настройки:

Когда-то давно в аналогичной ситуации я установил анализатор трафика и взял пароль из сетевого пакета. С тех пор поддержку нешифрованного подключения через pop3 на сервере отключили, и такой фокус уже не проходит.

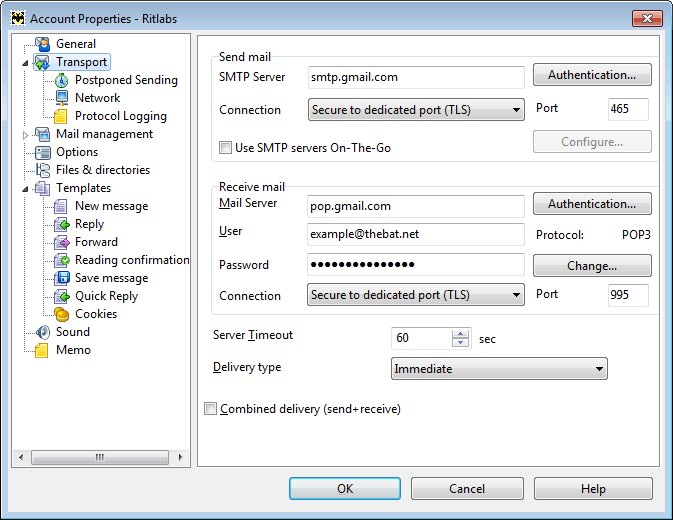
Я стал думать и сообразил, что фокус с перехватом трафика получился бы, если бы я подменил pop3-сервер на свой, который не требует никакого шифрования. К счастью, The Bat позволяет изменить сервер, не требуя повторного ввода пароля. Так что я ввел в это окошко локальный адрес, отключил шифрование и смог подключиться к локальному «серверу».

Чтобы не ставить настоящий сервер, нагуглил скрипт фейкового pop3-сервера. Вместе с этим пришлось узнать, что делает команда CAPA. У меня заработал такой вариант:

#!/usr/bin/env python
import socket

c = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
c.bind(('192.168.0.203',110))
c.listen(1)

while 1:
    csock, caddr = c.accept()
    cfile = csock.makefile('rw', 0)
    print "Connection accepted."
    cfile.write("+OK POP3 PROXY server ready mail.server.com\r\n")

    line = cfile.readline().strip()
    print "LINE: " + line
    cfile.write("+OK\r\nUSER\r\n.\r\n")

    line = cfile.readline().strip()
    print "LINE: " + line
    cfile.write("+OK\r\n")

    line = cfile.readline().strip()
    print "LINE: " + line
    cfile.write("+OK\r\n")

    line = cfile.readline().strip()
    print "LINE: " + line
    cfile.write("+OK\r\n")

    line = cfile.readline().strip()
    print "LINE: " + line
    cfile.write("+OK\r\n")

Запускается и после нажатия на кнопочку синхронизации выдает желаемый пароль. Даже трафик не нужно перехватывать:

roman@zeta:~$ sudo python pop3.py
Connection accepted.
LINE: CAPA
LINE: USER example
LINE: PASS password
LINE: STAT
LINE: QUIT

Серебристые облака — 5

Сегодня были хорошие условия для наблюдения серебристых облаков.

Кстати, а сегодня-то у этого сайта день рождения, 16 лет :)

Как додуматься до решения олимпиадной задачи?

Я иногда решаю «для себя» какие-нибудь сложные задачи по физике или математике. Практической пользы в этом нет, видимо, это мой способ проверить, что я всё еще не растерял форму. Ведь уже много времени прошло после красного диплома физтеха без четверок и серебряной медали с Международной олимпиады по физике.

Вчера решил очередную такую задачу из ролика Савватеева. Честно остановил ролик перед решением, задумался и нашел решение. Расскажу скорее не о самом решении, а о том, как можно его отыскать.

Условие задачи

В задаче требуется показать, что существует действительное число $$A\in\R$$, такое что любая натуральная степень $$n$$ этого числа после округления вверх отличается по модулю от ближайшего квадрата натурального числа ровно на 2.

Анализ условия

Запишем условие задачи формально: требуется доказать, что

$$\exists A\in\R\ \forall n\in\mathbb{N}\ \exists x\in\mathbb{N}:\left|\lceil A^n\rceil-x^2\right|=2.$$(1)

Здесь потерялось условие, что число $$x^2$$ должно быть ближайшим квадратом к $$\lceil A^n\rceil$$. Но оно будет выполнено автоматически, если $$A>5$$.

Условие выглядит страшно, и непонятно, как подступиться к задаче. В математике нет стандартных приемов по работе с округлением вверх. Придется пользоваться универсальным приемом: думать.

Перепишем условие менее формально. Для каждого $$n$$ должны найтись числа $$\varepsilon\in[0,1)$$ и $$x^2$$, для которых $$A^n+\varepsilon=x^2\pm2$$. При больших $$n$$ получаем, что $$A^n\approx x^2$$.

Озарение

Теперь самое время для озарения. Оно пришло ко мне в ходе такого рассуждения. Переход от $$n$$ к $$n+1$$ в левой части сводится к домножению на $$A$$, а в правой части — к переходу от одного квадрата к другому.

Квадраты натуральных чисел расположены по определенному шаблону. Разница между соседними квадратами — это последовательность нечетных чисел. Скорее всего в правой части при переходе от одного квадрата к другому прибавляется некоторое число, возможно связанное с $$A$$.

Вспоминаем, в каком случае домножение сводится к прибавлению? Есть известный пример для золотого сечения и для рекуррентных последовательностей типа Фибоначчи. Золотое сечение $$\varphi=(1+\sqrt5)/2$$ обладает свойством $$\varphi^{n+1}=\varphi^n+\varphi^{n-1}$$. То есть домножение $$\varphi^n$$ на $$\varphi$$ эквивалентно прибавлению $$\varphi^{n-1}$$. Возможно, число $$A$$ как-то связано с золотым сечением.

Гипотеза

Проверим гипотезу, что золотое сечение подходит на роль числа $$A$$. Вычислим для начальных $$n$$ степени золотого сечения и посмотрим, есть ли у них квадрат, отличающийся почти на 2:

$$n$$	$$\varphi^n$$	Квадрат
0	1,000000
1	1,618034
2	2,618034
3	4,236068
4	6,854102	9
5	11,090170
6	17,944272	16
7	29,034442
8	46,978714	49
9	76,013156
10	122,991869	121
11	199,005025
12	321,996894	324
13	521,001919
14	842,998814	841
15	1364,000733
16	2206,999547	2209

Для малых $$n$$ закономерности не видно. Но начиная с $$n=4$$ у каждого второго числа находится нужный квадрат! Наше вычисление показывает, что $$\varphi^2=2,\!618034$$ — неплохой кандидат для числа $$A$$. Оно подошло бы под условие, если бы не требование того, что именно ближайший квадрат, а не некоторый, должен отличаться на 2. Действительно, $$\varphi^2$$, округленное вверх до 3, отличается от квадрата 1² на 2. Чтобы учесть это требование, можем отобрать из таблицы не каждое второе число, а каждое четвертое, и положить $$A=\varphi^4$$.

Поскольку речь зашла о золотом сечении и числах Фибоначчи, мы можем понять, откуда в условии взялось округление вверх. Известно, что для чисел Фибоначчи $$F_{n}$$ есть формула Бине:

$$F_{n}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\varphi -(-\varphi )^{-1}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{2\varphi -1}}.$$

Для нашей задачи от нее толку мало, но она подсказывает, что мы можем добавить к иррациональному $$\varphi^n$$ какое-нибудь аналогичное убывающее слагаемое, чтобы получить целое число $$\lceil A^n\rceil$$. Слагаемое легко подобрать для конкретных чисел из таблицы или увидеть из разложения $$(1\pm\sqrt{5})^n$$ через бином Ньютона (например, видно, что $$(1+\sqrt{5})^n+(1-\sqrt{5})^n$$ целое, потому что при раскрытии скобок любые слагаемые с нечетными степенями корней взаимно сократятся из-за разных знаков). Но давайте подберем. $$\varphi^4=6,\!854102$$, отличается от 7 на 0,145898. Если обратить эту разность, опять получается $$\varphi^4=1/0,\!145898$$. Таким образом, $$\varphi^{4}+1/\varphi^{4}$$ должно быть целым числом. Обобщение этих наблюдений мы и будем строго доказывать.

Строгое доказательство

Докажем теперь, что $$\varphi^{2n}+\varphi^{-2n}$$ отличается от квадрата некоторого натурального числа на 2. Для этого рассмотрим вспомогательное число $$t_n=\varphi^{n}+(-\varphi)^{-n}$$.

Заметим, что $$(-\varphi)^{-1}=-2/(1+\sqrt{5})=(1-\sqrt{5})/2$$, как и $$\varphi$$, является решением уравнения $$y^{2}=y+1$$ и, следовательно, тоже удовлетворяет условию $$y^{n+1}=y^n+y^{n-1}$$. Итого имеем рекуррентную последовательность $$t_n=\varphi^{n}+(-\varphi)^{-n}$$, подчиняющуюся определению $$t_{n+1}=t_n+t_{n-1}$$, так как она есть сумма двух других рекуррентных последовательностей с тем же определением.

Вычислим начальные элементы последовательности $$t_n$$: $$t_0=1+1=2$$, $$t_1=(1+\sqrt{5})/2+(1-\sqrt{5})/2=1$$. По принципу математической индукции любой элемент последовательности $$t_n$$ — также целое число.

Возведем элемент последовательности $$t_n$$ в квадрат:

$$t^2_n=\left(\varphi^{n}+\left({-1\over\varphi}\right)^n\right)^2=\varphi^{2n}+{1\over\varphi^{2n}}+2(-1)^n.$$(2)

Таким образом, возведение $$\varphi^2$$ в степень $$n$$ и округление вверх дает целое число $$\varphi^{2n}+1/{\varphi^{2n}}$$, отличающееся от квадрата натурального числа $$|t_n|=|\varphi^{n}+(-\varphi)^{-n}|$$ ровно на 2.

Сравнение решения с авторским

Мое решение вроде бы завязано на золотое сечение и на его свойства. Но на самом деле используется только одно свойство: золотое сечение есть решение уравнения $$y^{2}=y+1$$. Сумма степеней корней этого уравнения порождает целочисленную последовательность. Есть и другие уравнения с тем же свойством. Корни по модулю должны быть взаимно обратными, чтобы сработало равенство наподобие (2). Можно было взять действительные корни любого уравнения $$y^{2}=ky\pm1$$ с целым $$k\neq\pm2$$.

Савватеев использовал свойства симметрических многочленов, чтобы показать целочисленность суммы степеней корней. Мой способ через математическую индукцию и рекуррентные последовательности тоже годится.

Анализ данных — В кресле препода №7

За последние несколько месяцев было крупных новостей, связанных с анализом данных. Мне как физику такие новости интересны и понятны, потому что современную физику нельзя представить без анализа данных. В очередном выпуске «В кресле препода» объясняю на конкретных примерах, как работает анализ и представление данных.

00:00 Резонансные новости, связанные с анализом данных
01:03 Анализ данных пришел из физики высоких энергий
02:25 Обработка данных с Большого адронного коллайдера
03:30 Настоящая Big Data на Большом адронном коллайдере: в «гриде» LHC идет запись 300 мегабайт данных в секунду
05:03 Визуализация и анализ данных на примере графика заболеваемости коронавирусом Яндекса
12:40 Как понять истинный масштаб заражений коронавирусом в России по избыточной смертности
19:38 Как распознать фальсификации на голосовании
29:39 Расследование Грозева об отравлении Навального
32:27 Анализ данных как современный научный метод против средневековой пропаганды

Алгоритмическая сложность

Одна из тем, которые я обязательно поднимаю на собеседовании, — это сложность алгоритмов. Кандидату на мои вакансии достаточно назвать сложность наилучшей сортировки — O(n·ln n). Еще о структурах данных речь заходит при обсуждении работы индексов БД. Кандидат должен объяснить, за счет чего индексы ускоряют выполнение запросов.

Если кандидат не дает ответа O(n·ln n), это тревожный звоночек. В зависимости от вакансии я могу еще попросить оценить сложность простейшей сортировки, например, пузырьком, чтобы отличить пробел в знаниях от неспособности понимать эту тему.

Почему важно иметь представление об алгоритмической сложности? Что будет, если писать код без этого представления? Недавно нашелся пример: если на рабочем столе создать 1000 файлов, Windows тратит 20 секунд на открытие главного меню. И всё потому, что какой-то криворукий программист написал алгоритм сложности O(n²) там, где можно было обойтись O(n). Подробности читайте на хабре.

← сюда туда →