математика

Статьи по этой теме:
Автоморфные числа
Деление окружности на 5 частей
Формула Эйлера и приближенные методы

---

Метод удвоения персонажей

Есть известный тип задач по математике, в которых несколько объектов движутся определенным образом, что-то о них известно, что-то требуется найти. Любую такую задачу можно решить универсальным методом, обозначив неизвестные величины переменными и составив систему уравнений. Но иногда с помощью подходящей иллюстрации или остроумного метода такие задачи можно решать в уме, без вычислений.

Откуда появился метод

Однажды коллега дал мне задачу на движение, якобы с собеседований (см. задачу №1 ниже). Чтобы упростить решение, я использовал метод (назовем его «удвоением персонажей»), о котором узнал из книжки Мартина Гарднера «Математические досуги». В ней сформулирована следующая задача:

Теорема о неподвижной точке. Однажды утром, как раз в тот момент, когда взошло солнце, один буддистский монах начал восхождение на высокую гору. Узкая тропа шириной не более одного-двух футов вилась серпантином по склону горы к сверкающему храму на ее вершине.

Монах шел по дорожке с разной скоростью; он часто останавливался, чтобы отдохнуть и поесть сушеных фруктов, которые взял с собой. К храму он подошел незадолго до захода солнца. После нескольких дней поста и размышлений монах пустился в обратный путь по той же тропе. Он вышел на рассвете и опять спускался с неодинаковой скоростью, много раз отдыхая по дороге. Средняя скорость спуска, конечно, превышала среднюю скорость подъема.

Докажите, что на тропе есть такая точка, которую монах во время спуска и во время подъема проходил в одно и то же время суток.

Решение задачи оказалось элегантным:

Человек поднимается на высокую гору и, пробыв несколько дней на вершине, спускается вниз. Найдется ли такая точка на тропе, которую оба раза он проходит в одно и то же время суток? Мое внимание на эту задачу обратил психолог из Орегонского университета Р. Хайман, который в свою очередь нашел ее в монографии, озаглавленной «О решении задач» и принадлежащей перу немецкого психолога Дункера. Дункер пишет, что сам он не смог решить задачу, и с удовлетворением отмечает, что никто из тех, кому он ее предлагал, тоже не добился успеха. Далее Дункер говорит о том, что существует много подходов к решению задачи, но, по его мнению, «самым очевидным является следующее объяснение. Пусть в один и тот же день по тропе идут два человека: один из них поднимается вверх, а второй спускается вниз. Они обязательно должны встретиться. Отсюда, как вы сами понимаете, следует, что… при таком подходе неясный вначале смысл задачи вдруг сразу становится совершенно очевидным».

Понятно, что в большинстве задач на движение за счет идеализации нет запутывающих сложностей: объекты движутся с постоянной скоростью, не тратят время на остановки и развороты. Но даже тогда приемы вроде перехода от ситуации с одним монахом к ситуации с двумя монахами упрощают рассуждения. Давайте посмотрим на примерах, как работает такой метод.

Задача №1

Человек хочет пройти через туннель для поездов. Пройдя четверть пути, он слышит приближающийся сзади поезд. Скорость поезда и расстояние до него неизвестны. Если человек развернется и побежит назад, то он достигнет начала туннеля одновременно с поездом. Если же человек побежит вперед, то конца туннеля он также достигнет одновременно с поездом. На сколько быстрее движется поезд по сравнению с человеком?

Решение через систему уравнений

Давайте для сравнения сначала решим задачу школьными методами.

Пусть скорость человека есть v, скорость поезда u, расстояние от поезда до тоннеля x, длина тоннеля y. В первой ситуации пока поезд проходит расстояние x до начала тоннеля, человек пробегает назад четверть y. Приравняем времена этих движений:

$${x\over u}={y/4\over v}.$$

Во второй ситуации до встречи поезд проходит сумму расстояний x и y, человек пробегает три четверти y. Аналогично получаем:

$${x+y\over u}={3y/4\over v}.$$

Вычитаем из второго уравнения первое:

$${y\over u}={2y/4\over v}={y\over 2v}.$$

Переменная x исчезла, у как ненулевая величина сокращается. Отсюда $$u=2v$$, то есть поезд в два раза быстрее.

Решение методом удвоения персонажей

Предположим, что через тоннель идет не один человек, а два. В момент обнаружения поезда первый бежит к началу тоннеля, а второй к концу.

$$\begin{tikzpicture}[font=\sffamily] \node[fill=green!20] (1) at (1.5,0.5) {1}; \node[fill=blue!20] (2) at (1.5,1) {2}; \draw[->] (1.west) -- ++(-0.5,0); \draw[->] (2.east) -- ++(0.5,0); \node[fill=red!30] at (-4,-0.5) {поезд}; \draw[semithick] (-5,0) -- (8,0); \foreach \x in {0,1.5,3,4.5,6} \draw (\x,0.1) -- (\x,-0.1); \draw[fill=yellow] (0,-0.035) rectangle ++(6,0.07); \end{tikzpicture}$$

Когда первый пробежал четверть тоннеля и добежал до его начала, второй тоже пробежал четверть и оказался в середине тоннеля. В этот момент поезд проезжает начало тоннеля.

$$\begin{tikzpicture}[font=\sffamily] \node[fill=green!20] at (0,0.5) {1}; \node[fill=blue!20] at (3,0.5) {2}; \node[fill=red!30] at (0,-0.5) {поезд}; \draw[semithick] (-5,0) -- (8,0); \foreach \x in {0,1.5,3,4.5,6} \draw (\x,0.1) -- (\x,-0.1); \draw[fill=yellow] (0,-0.035) rectangle ++(6,0.07); \end{tikzpicture}$$

Второму осталось бежать расстояние от середины тоннеля до конца, а поезду — проехать от начала тоннеля и до конца. По условию они делают это за одинаковое время.

$$\begin{tikzpicture}[font=\sffamily] \node[fill=green!20] at (0,0.5) {1}; \node[fill=blue!20] at (6,0.5) {2}; \node[fill=red!30] at (6,-0.5) {поезд}; \draw[semithick] (-5,0) -- (8,0); \foreach \x in {0,1.5,3,4.5,6} \draw (\x,0.1) -- (\x,-0.1); \draw[fill=yellow] (0,-0.035) rectangle ++(6,0.07); \end{tikzpicture}$$

Таким образом, поезд в два раза быстрее человека.

Сравнение методов

Ясно, что оба метода по своему смыслу одинаковы. Но рассуждения во втором методе не только наглядны, но и выстроены в одну линию. Ход рассуждений и временной ход событий из задачи совпадают. Поэтому при решении не нужно держать в голове сведения из всей задачи целиком, можно последовательно перебирать происходящие события.

Задача №2

Велосипедист едет вдоль железной дороги. Он заметил, что электрички, которые идут в ту же сторону, обгоняют его с интервалом в час, а электрички, которые идут в обратную сторону, встречаются ему с интервалом в полчаса. С каким интервалом электрички выходят с конечных станций?

Эту задачу разбирали в следующем ролике на канале GetAClass:

Давайте посмотрим, как применить в этой задаче метод удвоения персонажей.

Решение

В этой задаче нас путают электрички, которые едут в двух разных направлениях. Перейдем к эквивалентной задаче, в которой электрички едут только в одном направлении, но велосипедистов два. Первый, который едет по ходу движения электричек, встречает их раз в час, а второй — в противоположном направлении — раз в полчаса.

Пусть в начальный момент времени электричка и два велосипедиста находятся в одной точке.

$$\begin{tikzpicture}[font=\sffamily] \node[fill=green!20] (1) at (2,0.5) {1}; \node[fill=blue!20] (2) at (2,1) {2}; \draw[->] (1.east) -- ++(0.5,0); \draw[->] (2.west) -- ++(-0.5,0); \node[fill=red!30] at (2,-0.5) {электричка 1}; \draw[-,semithick] (-5,0) -- (8,0); \foreach \x in {0,2,4,6} \draw (\x,0.1) -- (\x,-0.1); \end{tikzpicture}$$

Через полчаса второй велосипедист, едущий назад, встречает следующую электричку. Запомним, что к этому моменту первый велосипедист проехал полчаса вперед. То есть расстояние между велосипедистами соответствует часу проходимого ими пути, назовем его «велосипедо-часом».

$$\begin{tikzpicture}[font=\sffamily] \node[fill=green!20] at (4,0.5) {1}; \node[fill=blue!20] at (0,0.5) {2}; \node[fill=red!30] at (0,-0.5) {электричка 2}; \draw[-,semithick] (-5,0) -- (8,0); \foreach \x in {0,2,4,6} \draw (\x,0.1) -- (\x,-0.1); \end{tikzpicture}$$

За следующие полчаса электричка проезжает этот «велосипедо-час», а также еще половину «велосипедо-часа», которую проезжает первый велосипедист.

$$\begin{tikzpicture}[font=\sffamily] \node[fill=green!20] at (6,0.5) {1}; \node[fill=blue!20] at (-2,0.5) {2}; \node[fill=red!30] at (6,-0.5) {электричка 2}; \draw[-,semithick] (-5,0) -- (8,0); \foreach \x in {0,2,4,6} \draw (\x,0.1) -- (\x,-0.1); \end{tikzpicture}$$

Теперь мы видим, что за последние полчаса электричка проезжает расстояние, в три раза большее, чем велосипедист, $$u=3v$$.

До второй половины решения задачи не так легко додуматься. Попробую объяснить, как к нему прийти. В условии есть некоторая неизменная величина — расстояние между соседними электричками. С ней проще работать в той системе отсчета, где электрички покоятся. То есть мы сейчас посмотрим на события глазами пассажиров электрички. Первый велосипедист движется в ту же сторону, что и мы, но мы в три раза быстрее. Скорость, с которой мы догоняем велосипедиста, равна двум велосипедным. Второй велосипедист движется на нас, и скорость сближения равна четырем велосипедным. К пассажирам на неподвижных станциях мы приближаемся с собственной скоростью, равной трем велосипедным скоростям. Нам будет казаться, что с этой скоростью они проносятся мимо нас назад. Получается, что одно и то же расстояние S между нами и следующей за нами электричкой первый велосипедист проходит с относительной скоростью 2v за час, второй с относительной скоростью 4v проходит за полчаса, а пассажиры на станции со скоростью 3v «преодолевают» за искомое время t. Запишем в виде уравнений:

$$S=2v\cdot 1,\quad S=4v\cdot{1\over 2},\quad S=3v\cdot t.$$

То, что первое и второе уравнения получились одинаковыми, показывает, что в первой половине решения ошибок не было. Из этих уравнений видно, что $$t=2/3$$ часа, или 40 минут.

Я бы не сказал, что до этого решения задачи додуматься проще всего. Можно было сразу записать систему уравнений с неизвестными скоростями $$(u-v)\cdot 1=(u+v)\cdot 0,\!5=u\cdot t$$ и решить ее относительно t. Но мне надо было на каком-то примере показать, как работает метод удвоения персонажей.

ChatGPT подсказал название задачи по формулировке

Недавно встретил редкую задачу из теории вероятностей. Сначала сам решил, потом стал спрашивать у ChatGPT, чтобы понять, под каким названием эта задача может быть известна.

Пусть имеется множество из N элементов. В ходе одного испытания случайным образом выбирается какой-либо элемент. Сколько в среднем нужно испытаний, чтобы каждый элемент множества был выбран хотя бы один раз?

ChatGPT в целом правильно воспроизводил идею решения, но с названием не заладилось. За несколько попыток правильного названия он так и не выдал, в каждой попытке какая-то ерунда:

Это классическая задача, известная как проблема дней рождения или задача выбора.

Это задача из теории вероятностей, известная как задача о парадоксе дней рождения или проблема обеспечения. В вашем случае, вы спрашиваете о среднем количестве испытаний, необходимых для того, чтобы выбрать каждый элемент множества хотя бы один раз. Это связано с так называемой задачей о шарах и ящиках.

Эта задача относится к классу задач под названием «задача об абсолютной перестановке» или «задача о деньгах дней рождения».

Этот вопрос относится к теории вероятностей и известен как проблема «парадокса дней рождений» или «проблема встречи». В вашем случае, это известно как проблема «выборки с возвратом» (sampling with replacement).

Этот вопрос связан с математической областью, называемой «парадоксом дней рождения» или «задачей о шарах и корзинах». Для вашего вопроса это называется «парадоксом выбора с возвращением».

Когда я добавил к своему запросу «ответ дай по-английски», получил правильное название:

This problem is a classic example of the coupon collector's problem.

Оказывается, эта интересная задача встречается в английской литературе под таким названием, что можно перевести как «задача коллекционера», а в русской литературе практически неизвестна. Я думал, что для ChatGPT не проблема дать ответ с учетом перевода. Но, видимо, при генерации ответа связь между словами одного языка сильнее, чем связи между терминами с учетом перевода.

О самой задаче коллекционера написал подробнее в «черновиках физика».

Еще одно решение задачи о педантичном пассажире

В прошлый раз я решал задачу о педантичном пассажире с помощью комбинаторных соображений и получил простой ответ: если один из пассажиров в автобусе захочет сидеть на своем месте, пересесть в среднем должна примерно половина автобуса. Напомню, что задача свелась к вычислению средней длины цикла в перестановке, содержащего некоторый элемент, например, 1.

Как я тогда и предположил, такой простой ответ можно получить почти без вычислений. Достаточно установить взаимно однозначное соответствие между перестановкой, описывающей рассадку пассажиров, и некоторой другой вспомогательной перестановкой, как изображено на схеме в примере:

$$\tikzcdset{arrow style=tikz,diagrams={>=stealth}} \begin{matrix} \left(\begin{tikzcd}[row sep=14pt,column sep=12pt] 1\ar[d] & 2\ar[d] & 3\ar[d] & 4\ar[d] & 5 & 6\ar[d] & 7 & 8 \\ \textcolor{blue}{4}\ar[urrr,dotted,looseness=1,in=155] & \textcolor{blue}{6}\ar[urrrr,dotted,looseness=1,in=160] & \textcolor{blue}{1}\ar[ull,dotted] & \textcolor{blue}{2}\ar[ull,dotted] & \bf{5} & \textcolor{blue}{3}\ar[ulll,dotted] & \bf{8} & \bf{7} \end{tikzcd}\right) &\longleftrightarrow& \begin{tikzcd}[column sep=8pt] \bf{5} & \bf{8} & \bf{7} & \textcolor{blue}{1}\ar[r,dotted] & \textcolor{blue}{4}\ar[r,dotted] & \textcolor{blue}{2}\ar[r,dotted] & \textcolor{blue}{6}\ar[r,dotted] & \textcolor{blue}{3}\ar[llll,dotted,looseness=0.5,in=-60,out=-120] \end{tikzcd} \end{matrix}$$

Здесь я нарисовал стрелками, как в цикле переходят элементы друг в друга. Чтобы получить вспомогательную перестановку, нужно переместить в конец элементы цикла, содержащего элемент 1, начиная как раз с него.

От вспомогательной перестановки всегда можно перейти к изначальной, рассматривая элемент 1 и соседей справа от него как сокращенную запись цикла. Разворачиваем запись цикла и расставляем соседей слева на оставшиеся свободные места.

Таким образом, мы установили биекцию (взаимно однозначное соответствие) между перестановками, при которой элементы цикла, содержащего элемент 1, переходят в элемент 1 и всех соседей справа. При усреднении по всем перестановкам любой элемент, в том числе 1, оказывается в середине (на каждую перестановку, где этот элемент сдвинут влево от центра, есть зеркальная перестановка, где он сдвинут на такое же расстояние вправо). Поэтому среднее количество соседей слева и справа совпадает и равно $$(n-1)/2$$.

Вспомогательную перестановку следует воспринимать формально, она сама по себе в этой задаче не имеет наглядного смысла.

Чему же равно 6:2(1+2)?

Когда я впервые увидел этот пример в интернете, подумал, что это проблема на ровном месте. Да, мнения людей об ответе расходятся: кто-то отвечает 1, а кто-то 9. Но в реальности никакой путаницы не бывает, хотя бы потому, что деление обозначается двоеточием разве что в школе. В книгах и статьях формулы с делением записываются в виде дроби, и сначала нужно выполнить действия в числителе (над чертой) и в знаменателе (под чертой), и только потом выполнять деление, обозначаемое чертой. С такой записью разночтений нет:

$${6\over 2(1+2)}={6\over 6}=1.$$

Борис Трушин смог снять по этой теме целых два видео по 18 минут:

После просмотра я сделал для себя такой вывод. Приоритет арифметических действий учат в начальной школе, а опускать знак умножения — только в средней школе. По характеру необходимых действий пример 6:2(1+2) — из начальной школы, поэтому он записан некорректно, умножение между двойкой и скобками опускать нельзя.

И совсем недавно мне попалось еще одно видео по теме. Оказывается, мнение о правильном ответе расходятся не только у спорящих в интернете, но и у производителей калькуляторов!

В этом видео отметил следующие вещи. Оказывается, около 100 лет назад еще были колебания в определении приоритета (явного) умножения и деления, но колебания приоритета неявного умножения над делением не было: если знак умножения опущен, выражение воспринимается единым целым, будто записано в скобках. К девяностым годам североамериканские учителя повлияли на производителей калькуляторов, чтобы те изменили приоритет неявного умножения и выровняли его с явным умножением и делением. Но так сделали не все производители, а сейчас происходит частичный откат к тому, что неявное произведение становится приоритетнее. Колебания приоритета неявного умножения относятся только обучению в школе, в профессиональном употреблении колебаний нет.

После просмотра этого видео я понял, что мой аргумент про использование двоеточия как знака деления в основном в начальной школе — это всего лишь отрицание проблемы. Действительно, использование горизонтальной черты для обозначения деления удобно в отдельных формулах, а не в сплошном тексте. Сейчас в математических текстах вместо двоеточия используется наклонная черта. Так что никто не мешает спросить, чему равно 6/2(1+2).

Я решил посмотреть, как сам записывал в одну строку формулы с делением и неявным умножением, и какие приоритеты подразумевал. Прошелся по текстам в блоге о теоретической физике старше нескольких лет, чтобы исключить возможное влияние обсуждений этого вирусного примера. В выражении (5/4) v/R взял в скобки числовой множитель, чтобы показать, что получившаяся величина на четверть больше некоторой характерной угловой скорости v/R. При этом (5/4) v/R ≠ 5/4v/R = 5/4vR. По тем же соображениям использовал скобки в (4π/c) j, здесь так же (4π/c) j = 4πj/c ≠ 4π/cj. В выражении v/(pR) оставил в знаменателе скобки для понятности, их можно было бы убрать. И, наконец, c²/4G. Здесь и 4, и G в знаменателе, c²/4G ≠ c²G/4. Получается, я вполне последовательно использовал неявное умножение с более высоким приоритетом, чем деление, хотя и не могу вспомнить, что подобному правилу нас учили так же, как, например, формуле для решения квадратного уравнения.

Раз уж мы обсуждаем приоритеты арифметических действий, поделюсь воспоминанием из начальной школы, кажется, из второго класса. Учительница нам говорила, что если в выражении на одном уровне несколько умножений и делений, то выполняются сначала деления, а потом умножения. Такого правила я больше нигде не встречал. Обычно учат, что умножение и деление выполняется подряд, слева направо. Например, 8/4×10/2 = 2×10/2 = 20/2 = 10. Если воспользоваться «странным» правилом о приоритете деления над умножением, тоже получится 8/4×10/2 = 2×5 = 10. При этом нельзя, например, сначала выполнить все умножения, а потом все деления. В нашем примере получилось бы 8/(4×10)/2 = 8/40/2 = 0,1, что не совпадает с правильным ответом. Как вы думаете, всегда ли «странное» правило приоритета деления над умножением приводит к тем же результатам, что и обычное правило? Или сможете найти контрпример?

Задача о педантичном пассажире

В недавней поездке наблюдал, как люди рассаживаются в автобусе. Чтобы скоротать время в дороге, решил прикинуть, насколько тяжело пересаживаться людям, занимающим места не по билетам. Задачу пришлось решать в уме, так как черновика и ручки не было. Правда, был мобильник с интернетом, так что без чтения википедии и других сайтов не обошлось. Однако ничего полезного не нашел и решил задачу самостоятельно.

Условие

В автобусе n пронумерованных мест. Пассажиры занимают места в случайном порядке, не обращая внимание на номера в билетах. Последний пассажир оказывается педантичным — он хочет сидеть на своем месте. Если место педантичного пассажира занято, он заставляет сидящего там пассажира пересесть. Пересаживающийся пассажир тоже становится педантичным и идет на свое место. Процесс пересаживания продолжается до тех пор, пока последний педантичный пассажир не усядется в пустое место. Сколько в среднем пассажиров пересядет?

Математическая природа задачи

Знакомые с теорией представлений групп перестановок сразу скажут, какая идея скрывается за формулировкой задачи. Мне же придется пересказать некоторые математические факты, чтобы пояснить ход рассуждений.

Сидящие в каком-то порядке пассажиры описываются перестановкой — отображением множества из n элементов на это же множество. Действительно, каждая рассадка пассажиров задает взаимно однозначное соответствие (биективную функцию) номеров мест на номера билетов пассажиров. Рассмотрим пример из задачи для n=8:

$$\begin{pmatrix} \text{места}\\ \text{билеты} \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 4 & 6 & \bf{1^*} & 2 & 5 & 3 & 8 & 7 \end{pmatrix}.$$

Для удобства рассуждений будем считать, что педантичный пассажир имеет билет номер 1. (Интуитивно понятно, что ответ в задаче не зависит от конкретного номера билета у педантичного пассажира, но вы попробуйте это доказать в качестве упражнения.) Если бы пассажир не был педантичным, он просто занял бы свободное место с номером 3. Но поскольку пассажир педантичный, он заставляет пересесть пассажира 4, тот заставляет пересесть пассажира 2, дальше пересаживается пассажир 6 и, наконец, пассажир 3 идет на свое свободное место:

$$\tikzcdset{arrow style=tikz,diagrams={>=stealth}} \begin{matrix} \left(\begin{tikzcd}[row sep=14pt,column sep=12pt] 1\ar[d] & 2\ar[d] & 3\ar[d] & 4\ar[d] & 5 & 6\ar[d] & 7 & 8 \\ 4\ar[urrr,dotted,looseness=1,in=155] & 6\ar[urrrr,dotted,looseness=1,in=160] & 1\ar[ull,dotted] & 2\ar[ull,dotted] & 5 & 3\ar[ulll,dotted] & 8 & 7 \end{tikzcd}\right) \end{matrix}$$

Получившаяся цепочка (1 4 2 6 3) называется циклом.

Таким образом, в задаче фактически нужно найти среднюю длину цикла, содержащего случайно выбранный элемент случайной перестановки.

Погружение в теорию

Любая перестановка распадается на один или несколько циклов. В нашем примере это циклы $$(1\ 4\ 2\ 6\ 3)(5)(7\ 8)$$. Циклы могут иметь произвольную положительную длину. Единственное ограничение на циклы — сумма их длин равна n. Фактически циклическая структура перестановки описывается разбиением чисел.

Разбиения чисел, как и циклы в перестановках, изображают графически в виде диаграмм Юнга. Каждая строка этой диаграммы соответствует своему циклу, строки расположены в порядке убывания длины. В нашем примере диаграмма Юнга имеет вид:

$$\begin{tikzpicture}[scale=0.5]\small \draw[line width=0.22mm] (0,0) grid (5,-1) (0,-1) grid (2,-2) (0,-2) grid (1,-3); \end{tikzpicture}$$

Каждой диаграмме Юнга, в которой $$m_1$$ циклов длины 1, $$m_2$$ циклов длины 2 и т. д. соответствует следующее количество перестановок:

$$N={n!\over 1^{m_1}m_1!\cdot 2^{m_2}m_2!\cdot\ldots\cdot n^{m_n}m_n!}.$$

Давайте для тренировки проверим, что получится для нашей диаграммы Юнга:

$$N_{8 = 5 + 2 + 1}={8!\over 1^{1}1!\cdot 2^{1}1!\cdot 5^{1}1!}={8!\over 10}=4032.$$

Выходит, среди всех 8! = 40320 перестановок из 8 элементов десятая часть имеет структуру, описываемую разбиением 8 = 5 + 2 + 1.

Теперь надо перебрать все диаграммы Юнга, для каждой вычислить вес по этой формуле и усреднить длину строк с такими коэффициентами. Осталась «небольшая» проблема — я не знаю простого аналитического способа перебора диаграмм Юнга. Такой метод решения задачи заводит в тупик, особенно если решать в уме. Поэтому забудем всё, что здесь было написано, и будем решать задачу с нуля без каких-либо предварительных знаний о циклах.

Решение «на пальцах»

Как было написано выше, мы будем вычислять среднюю длину цикла, содержащего первый элемент в случайной перестановке длины n. (Вместо первого элемента можно брать любой: из формул дальше видно, что ответ от этого не зависит.) Под средней длиной понимается математическое ожидание — усреднение длины цикла с весами, равными вероятностям:

$$L=P_1\cdot 1+P_2\cdot 2 +\ldots+P_n\cdot n,$$

где $$P_1$$ — вероятность того, что цикл имеет длину 1, $$P_2$$ — что имеет длину 2 и т. д. Ясно, что циклов с длиной больше чем полное количество элементов n не бывает, и слагаемые в формуле останавливаются на n.

В этой формуле легко подсчитать $$P_1$$. Так как перестановки случайные, элемент 1 с равной вероятностью может переводиться перестановкой в любой другой элемент от 1 до n. Если 1 переходит в 1, мы получаем цикл длины 1:

$$\begin{pmatrix} 1 & 2 & \ldots & n\\ 1 & * & \ldots & * \end{pmatrix}.$$

В противном случае длина цикла будет больше. Таким образом, $$P_1=1/n$$ — с такой вероятностью можно выбрать число 1 из первых n чисел.

Попробуем теперь вычислить $$P_2$$. Чтобы получился цикл длины 2, элемент 1 должен переходить в элемент $$k\neq 1$$, а элемент k — в 1:

$$\begin{pmatrix} 1 & \ldots & k & \ldots & n\\ k & \ldots & 1 & \ldots & *\\ \end{pmatrix}.$$

Есть $$n-1$$ способ выбрать первый элемент $$k\neq1$$, что дает вероятность $$(n-1)/n$$ (действительно, в противном случае мы бы получили цикл длины 1 с вероятностью $$P_1=1/n$$). Вторым элементом должен быть 1, его можно выбрать из оставшихся $$n-1$$ элементов с вероятностью $$1/(n-1)$$. Таким образом,

$$P_2={n-1\over n}\cdot{1\over n-1}={1\over n}.$$

Удивительно, но мы получили, что $$P_1=P_2=1/n$$. Давайте проверим, совпадение ли это, или закономерность. Цикл будет иметь длину 3, если его длина не 1 и не 2, и если третьим элементом мы выберем 1. Вероятность этого

$$P_3=\left(1-P_1-P_2\right)\cdot{1\over n-2}={n-2\over n}\cdot{1\over n-2}={1\over n}.$$

Аналогично все остальные вероятности тоже совпадают: $$P_i=1/n$$. Таким образом, средняя длина цикла $$L=(n+1)/2$$.

Вывод

В автобусе с количеством мест n педантичный пассажир спровоцирует $$(n+1)/2$$ пересадок. Или, если исключить его самого из этого числа, пересядет $$(n-1)/2$$ других пассажиров. Мы не только вычислили среднее количество пересаживающихся пассажиров, а еще и нашли распределение этого количества: оно оказалось равномерным. Иными словами, с равной вероятностью педантичный пассажир сядет в свое пустое место, или заставит пересесть одного пассажира, или двух и т. д. Все эти исходы оказываются равновероятными.

Послесловие

Простота ответа — пересесть должна половина автобуса — наводит на мысль о том, что задачу можно решить только с помощью некоторой наглядной картинки, вообще без вычислений. К сожалению, я пока не придумал, как это сделать. Например, можно мысленно переставить сиденья с пассажирами в один ряд так, чтобы в процессе пересаживания педантичный пассажир садился на случайное место, заставляя пересесть всех пассажиров справа от него на одно место. Ясно, что для такой вставки элемента среднее количество операций совпадает с вычисленным ответом. Но откуда возьмется связь между случайным циклом случайной перестановки и элементами справа от случайно выбранного элемента? Как между ними установить соответствие, сохраняющее вероятности?

И, наконец, если вы сомневаетесь в правильности ответа, можете запустить скрипт, вычисляющий ответ методом полного перебора. Алгоритм перебора перестановок взял из книжки. Сконвертировал код из Perl в PHP с помощью ChatGPT. Усреднение длины цикла делается тривиально.

<?php

function nextShuffle(array $shuffle): ?array {
    for ($i = 1, $count = count($shuffle); $i < $count; $i++) {
        if ($shuffle[$i] < $i) {
            $shuffle[$i]++;
            return $shuffle;
        }

        $shuffle[$i] = 0;
    }
    return null;
}

// Длина цикла, содержащего элемент 1.
function cycleLength(array $p): int {
    $num    = 1;
    $result = 0;
    while ($p[$num - 1] !== 1) {
        $num = $p[$num - 1];
        $result++;
    }
    return $result;
}

$n = (int)$argv[1];
if ($n <= 0) {
    die("$argv[0]: Нужно неотрицательное число!\n");
}

$shuffle = array_fill(0, $n, 0);

$totalLength       = 0;
$totalPermutations = 0;
while ($shuffle !== null) {
    // Начальная перестановка
    $p = range(1, $n);
    // Применение транспозиций
    for ($i = 0; $i < $n; $i++) {
        $temp            = $p[$i];
        $p[$i]           = $p[$shuffle[$i]];
        $p[$shuffle[$i]] = $temp;
    }

    $length      = cycleLength($p);
    $totalLength += $length;
    $totalPermutations++;
    // echo implode(" ", $p), "  | ", $length, "\n";

    // Генерирование следующего набора транспозиций
    $shuffle = nextShuffle($shuffle);
}

echo "Всего перестановок (факториал) = ", $totalPermutations, "\n", 
     "Среднее количество пересадок = ", $totalLength / $totalPermutations, "\n";

Пример результата запуска:

> php script.php 8
Всего перестановок (факториал) = 40320
Среднее количество пересадок = 3.5

Как додуматься до решения олимпиадной задачи — 2

В прошлый раз я рассказывал о ходе своих мыслей при решении олимпиадной задачи. Может быть такие рассказы помогут кому-нибудь, кто хочет выработать нестандартное мышление. В этот раз расскажу о ходе решения еще одной задачи, которую разбирал Савватеев. По его словам, за 5 минут он решения не нашел, и зрителям думать не советовал. Но я не послушал и додумался до решения самостоятельно.

Условие задачи

Есть 3 различных натуральных числа $$x$$, $$y$$, $$z$$. Эти числа оказались подобраны так, что выражение

$$A={xy+yz+zx\over x+y+x}$$

тоже натуральное. Каким числом оно может быть? Иными словами, каково пересечение множества значений этой функции трех натуральных переменных и множества натуральных чисел?

Поиск решения

Идея №1: вынести в числителе за скобки $$xyz$$. Получается

$$A={\left({1\over x}+{1\over y}+{1\over z}\right)xyz\over x+y+x}.$$

Из этого я заметил, что при замене величин $$x$$, $$y$$ и $$z$$ на обратные $$1/x$$, $$1/y$$ и $$1/z$$ выражение «переворачивается», то есть $$A$$ меняется на $$1/A$$. Дальше у идеи не было очевидного развития, я решил попробовать другие идеи.

Идея №2: масштабирование. Видно, что если выполнить замену $$x$$, $$y$$ и $$z$$ на $$kx$$, $$ky$$ и $$kz$$, то числитель $$A$$ вырастет в $$k^2$$ раз, а знаменатель в $$k$$ раз, то есть $$A$$ меняется на $$kA$$. Как это можно применить? Пусть мы выбрали натуральные числа равными 1, 2 и 3. Тогда

$$A={2+6+3\over 1+2+3}={11\over 6}.$$

Чтобы из этого набора получить целое $$A=11$$, можно взять не 1, 2 и 3, а 6, 12 и 18.

Однако я не стал развивать дальше эту идею из-за ошибки. Мне показалось, что $$A$$ меняется не на $$kA$$, а на $$k^2A$$, и я пропустил условие, что числа могут быть различными. Так что мне показалось, что, подставив $$x=y=z=1$$, можно получить квадраты натуральных чисел 1, 4, 9,… Я понимал, что задача не такая простая, поэтому хотел проанализировать случай различных $$x$$, $$y$$ и $$z$$ (хотя по условию только их и надо анализировать), и перешел к дальнейшему рассмотрению.

Идея №3: перебор вариантов.

Чтобы прочувствовать задачу, часто бывает полезно рассмотреть некоторые частные случаи. В задачах вроде этой подобрать $$x$$, $$y$$ и $$z$$, чтобы выражение действительно было целым. В геометрических задачах бывает полезно нарисовать на черновике хороший чертеж, чтобы заметить закономерности вроде расположения точек на одной прямой или окружности.

Для перебора будем фиксировать значения $$x$$, $$y$$ и изменять $$z$$. Пусть $$x=y=1$$ (я проделал эту лишнюю работу, потому что невнимательно прочитал условие).

$$A={1+z+z\over 1+1+z}={1+2z\over 2+z}={4+2z-3\over 2+z}=2-{3\over 2+z}.$$

Ясно, что $$A=1$$ при $$z=1$$, а значение $$A=2$$ ни при каком $$z$$ не будет достигнуто.

Пусть $$x=1, y=2$$. Тогда

$$A={2+2z+z\over 1+2+z}={2+3z\over 3+z}.$$

Если $$z$$ нечетное, то числитель нечетный, знаменатель четный, $$A$$ не будет целым. Если $$z$$ четное, то числитель четный, знаменатель нечетный. Здесь я сделал еще одну ошибку, подумав, что четное число не может делиться на нечетное, и вообще исключил из рассмотрения варианты с $$x$$ и $$y$$ разной четности.

Пусть $$x=1, y=3$$. Тогда

$$A={3+3z+z\over 1+3+z}={3+4z\over 4+z}.$$

Здесь исключаем случай четного $$z$$, так как нечетный знаменатель не будет делиться на четный числитель. Попробуем подставить разные нечетные $$z$$. Получим:

$$ z=1\implies A={7/5}\\ z=3\implies A={12/7}\\ z=5\implies A={23/9}\\ z=7\implies A={31/11}\\ z=9\implies A={39/13}=3\\ z=11\implies A={47/15}\\ $$

Далее, сколько бы мы ни увеличивали $$z$$, до значения 4 мы не дойдем, так как 4 достигается только в пределе $$z\to\infty$$. Таким образом, при $$x=1, y=3$$ единственное целое $$A$$ дает $$z=9$$.

Пусть $$x=1, y=5$$. Тогда

$$A={5+5z+z\over 1+5+z}={5+6z\over 6+z}.$$

Перебор $$z$$ слишком долгий, и мы понимаем, что возможных значений $$A$$ не так уж много. Поэтому решим уравнение относительно $$z$$:

$$5+6z=A(6+z)\iff(6-A)z=6A-5\implies z={6A-5\over 6-A}.$$

Отсюда видно, что $$A$$ не может быть четным. 1 и 3 не подходят, $$A=5$$ дает $$z=25$$, других значений для проверки нет.

Мы видим, что значения переменных (1, 3, 9) и (1, 5, 25) дают целые значения $$A$$. Кажется, это и есть нужная закономерность.

Решение

Подставим значения $$x=1, y=n, z=n^2$$. Тогда

$$A={n+n^3+n^2\over 1+n+n^2}=n\,{1+n^2+n\over 1+n+n^2}=n.$$

Таким образом, мы можем в качестве значения выражения получить любое натуральное число, не равное 1. То, что 1 получить нельзя, посмотрите у Савватеева или докажите самостоятельно.

Обсуждение ошибок

После подстановки $$x=1, y=n, z=n^2$$ моя ошибка с четностью стала очевидной. Сначала мне вообще не хотелось писать об ошибках. Признаваться в них не очень приятно. Но с другой стороны, благодаря ошибкам на этапе поиска решения я довольно быстро нашел правильное решение. Могло бы оказаться так, что я углубился в разработку какой-нибудь другой тупиковой идеи и не довел бы решение до конца. Особенно важно такое чутье на самой олимпиаде в условиях ограниченного времени.

Чтобы минимизировать ошибки на олимпиадах, важно не переписывать решение с черновика на чистовик, а заново решить задачу на чистовике, обращаясь к черновику только для сравнения вычислений. Об этом и других советах я уже писал в руководстве олимпиадника.

Савватеев и Шпилькин разбирают статистику с выборов

Сергей Шпилькин — это тот самый физик, который обрабатывает математическими методами данные с выборов. Если вы до сих пор не читали и не разбирались в его результатах, посмотрите, как они с Савватеевым обсуждают графики, гипотезы и вообще применимость к выборам математических методов как таковых.

Пару раз они забылись и произнесли понятные только специалистам термины вроде «минимального детерминанта матрицы ковариации», но на восприятии основного посыла это не сказалось.

Как додуматься до решения олимпиадной задачи?

Я иногда решаю «для себя» какие-нибудь сложные задачи по физике или математике. Практической пользы в этом нет, видимо, это мой способ проверить, что я всё еще не растерял форму. Ведь уже много времени прошло после красного диплома физтеха без четверок и серебряной медали с Международной олимпиады по физике.

Вчера решил очередную такую задачу из ролика Савватеева. Честно остановил ролик перед решением, задумался и нашел решение. Расскажу скорее не о самом решении, а о том, как можно его отыскать.

Условие задачи

В задаче требуется показать, что существует действительное число $$A\in\R$$, такое что любая натуральная степень $$n$$ этого числа после округления вверх отличается по модулю от ближайшего квадрата натурального числа ровно на 2.

Анализ условия

Запишем условие задачи формально: требуется доказать, что

$$\exists A\in\R\ \forall n\in\mathbb{N}\ \exists x\in\mathbb{N}:\left|\lceil A^n\rceil-x^2\right|=2.$$(1)

Здесь потерялось условие, что число $$x^2$$ должно быть ближайшим квадратом к $$\lceil A^n\rceil$$. Но оно будет выполнено автоматически, если $$A>5$$.

Условие выглядит страшно, и непонятно, как подступиться к задаче. В математике нет стандартных приемов по работе с округлением вверх. Придется пользоваться универсальным приемом: думать.

Перепишем условие менее формально. Для каждого $$n$$ должны найтись числа $$\varepsilon\in[0,1)$$ и $$x^2$$, для которых $$A^n+\varepsilon=x^2\pm2$$. При больших $$n$$ получаем, что $$A^n\approx x^2$$.

Озарение

Теперь самое время для озарения. Оно пришло ко мне в ходе такого рассуждения. Переход от $$n$$ к $$n+1$$ в левой части сводится к домножению на $$A$$, а в правой части — к переходу от одного квадрата к другому.

Квадраты натуральных чисел расположены по определенному шаблону. Разница между соседними квадратами — это последовательность нечетных чисел. Скорее всего в правой части при переходе от одного квадрата к другому прибавляется некоторое число, возможно связанное с $$A$$.

Вспоминаем, в каком случае домножение сводится к прибавлению? Есть известный пример для золотого сечения и для рекуррентных последовательностей типа Фибоначчи. Золотое сечение $$\varphi=(1+\sqrt5)/2$$ обладает свойством $$\varphi^{n+1}=\varphi^n+\varphi^{n-1}$$. То есть домножение $$\varphi^n$$ на $$\varphi$$ эквивалентно прибавлению $$\varphi^{n-1}$$. Возможно, число $$A$$ как-то связано с золотым сечением.

Гипотеза

Проверим гипотезу, что золотое сечение подходит на роль числа $$A$$. Вычислим для начальных $$n$$ степени золотого сечения и посмотрим, есть ли у них квадрат, отличающийся почти на 2:

$$n$$	$$\varphi^n$$	Квадрат
0	1,000000
1	1,618034
2	2,618034
3	4,236068
4	6,854102	9
5	11,090170
6	17,944272	16
7	29,034442
8	46,978714	49
9	76,013156
10	122,991869	121
11	199,005025
12	321,996894	324
13	521,001919
14	842,998814	841
15	1364,000733
16	2206,999547	2209

Для малых $$n$$ закономерности не видно. Но начиная с $$n=4$$ у каждого второго числа находится нужный квадрат! Наше вычисление показывает, что $$\varphi^2=2,\!618034$$ — неплохой кандидат для числа $$A$$. Оно подошло бы под условие, если бы не требование того, что именно ближайший квадрат, а не некоторый, должен отличаться на 2. Действительно, $$\varphi^2$$, округленное вверх до 3, отличается от квадрата 1² на 2. Чтобы учесть это требование, можем отобрать из таблицы не каждое второе число, а каждое четвертое, и положить $$A=\varphi^4$$.

Поскольку речь зашла о золотом сечении и числах Фибоначчи, мы можем понять, откуда в условии взялось округление вверх. Известно, что для чисел Фибоначчи $$F_{n}$$ есть формула Бине:

$$F_{n}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\varphi -(-\varphi )^{-1}}}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{2\varphi -1}}.$$

Для нашей задачи от нее толку мало, но она подсказывает, что мы можем добавить к иррациональному $$\varphi^n$$ какое-нибудь аналогичное убывающее слагаемое, чтобы получить целое число $$\lceil A^n\rceil$$. Слагаемое легко подобрать для конкретных чисел из таблицы или увидеть из разложения $$(1\pm\sqrt{5})^n$$ через бином Ньютона (например, видно, что $$(1+\sqrt{5})^n+(1-\sqrt{5})^n$$ целое, потому что при раскрытии скобок любые слагаемые с нечетными степенями корней взаимно сократятся из-за разных знаков). Но давайте подберем. $$\varphi^4=6,\!854102$$, отличается от 7 на 0,145898. Если обратить эту разность, опять получается $$\varphi^4=1/0,\!145898$$. Таким образом, $$\varphi^{4}+1/\varphi^{4}$$ должно быть целым числом. Обобщение этих наблюдений мы и будем строго доказывать.

Строгое доказательство

Докажем теперь, что $$\varphi^{2n}+\varphi^{-2n}$$ отличается от квадрата некоторого натурального числа на 2. Для этого рассмотрим вспомогательное число $$t_n=\varphi^{n}+(-\varphi)^{-n}$$.

Заметим, что $$(-\varphi)^{-1}=-2/(1+\sqrt{5})=(1-\sqrt{5})/2$$, как и $$\varphi$$, является решением уравнения $$y^{2}=y+1$$ и, следовательно, тоже удовлетворяет условию $$y^{n+1}=y^n+y^{n-1}$$. Итого имеем рекуррентную последовательность $$t_n=\varphi^{n}+(-\varphi)^{-n}$$, подчиняющуюся определению $$t_{n+1}=t_n+t_{n-1}$$, так как она есть сумма двух других рекуррентных последовательностей с тем же определением.

Вычислим начальные элементы последовательности $$t_n$$: $$t_0=1+1=2$$, $$t_1=(1+\sqrt{5})/2+(1-\sqrt{5})/2=1$$. По принципу математической индукции любой элемент последовательности $$t_n$$ — также целое число.

Возведем элемент последовательности $$t_n$$ в квадрат:

$$t^2_n=\left(\varphi^{n}+\left({-1\over\varphi}\right)^n\right)^2=\varphi^{2n}+{1\over\varphi^{2n}}+2(-1)^n.$$(2)

Таким образом, возведение $$\varphi^2$$ в степень $$n$$ и округление вверх дает целое число $$\varphi^{2n}+1/{\varphi^{2n}}$$, отличающееся от квадрата натурального числа $$|t_n|=|\varphi^{n}+(-\varphi)^{-n}|$$ ровно на 2.

Сравнение решения с авторским

Мое решение вроде бы завязано на золотое сечение и на его свойства. Но на самом деле используется только одно свойство: золотое сечение есть решение уравнения $$y^{2}=y+1$$. Сумма степеней корней этого уравнения порождает целочисленную последовательность. Есть и другие уравнения с тем же свойством. Корни по модулю должны быть взаимно обратными, чтобы сработало равенство наподобие (2). Можно было взять действительные корни любого уравнения $$y^{2}=ky\pm1$$ с целым $$k\neq\pm2$$.

Савватеев использовал свойства симметрических многочленов, чтобы показать целочисленность суммы степеней корней. Мой способ через математическую индукцию и рекуррентные последовательности тоже годится.

Редактор математических текстов Mathcha

Искал онлайн-инструменты для редактирования картинок TikZ и наткнулся на редактор Mathcha.

Этот редактор — визуальный: вы сразу редактируете документ вместе с форматированием. В отличие от моего редактора Upmath, в котором вы редактируете исходник на маркдауне и латехе, хотя и сразу видите результат.

Вот рисунок, который я сделал с помощью Mathcha. Накидал основу в нем, экспортировал в TikZ и подправил исходный код уже в UpMath.

$$ \tikzset{every picture/.style={line width=0.75pt}} %set default line width to 0.75pt \begin{tikzpicture}[x=0.75pt,y=0.75pt,yscale=-1,xscale=1] %uncomment if require: \path (0,300); %set diagram left start at 0, and has height of 300 %Shape: Boxed Line [id:dp7642567693966007] \draw (130,80) -- (130,140) ; %Shape: Boxed Line [id:dp02318954146147889] \draw (130,150) -- (130,180) ; %Shape: Boxed Line [id:dp4638027067588357] \draw (130,190) -- (130,250) ; %Shape: Wave [id:dp03622557580885122] \draw [color={rgb, 255:red, 74; green, 144; blue, 226 } ,draw opacity=1 ] (215,80) .. controls (202.19,83.1) and (190,86.06) .. (190,89.5) .. controls (190,92.94) and (202.19,95.9) .. (215,99) .. controls (227.81,102.1) and (240,105.06) .. (240,108.5) .. controls (240,111.94) and (227.81,114.9) .. (215,118) .. controls (202.19,121.1) and (190,124.06) .. (190,127.5) .. controls (190,130.94) and (202.19,133.9) .. (215,137) .. controls (227.81,140.1) and (240,143.06) .. (240,146.5) .. controls (240,149.94) and (227.81,152.9) .. (215,156) .. controls (202.19,159.1) and (190,162.06) .. (190,165.5) .. controls (190,168.94) and (202.19,171.9) .. (215,175) .. controls (227.81,178.1) and (240,181.06) .. (240,184.5) .. controls (240,187.94) and (227.81,190.9) .. (215,194) .. controls (202.19,197.1) and (190,200.06) .. (190,203.5) .. controls (190,206.94) and (202.19,209.9) .. (215,213) .. controls (227.81,216.1) and (240,219.06) .. (240,222.5) .. controls (240,225.94) and (227.81,228.9) .. (215,232) .. controls (202.19,235.1) and (190,238.06) .. (190,241.5) .. controls (190,244.57) and (199.7,247.26) .. (210.89,250) ; %Straight Lines [id:da008457960885399407] \draw (190,80) -- (190,250) ; %Flowchart: Summing Junction [id:dp09695643217509597] \draw (135,132.75) .. controls (135,128.75) and (138.36,125.5) .. (142.5,125.5) .. controls (146.64,125.5) and (150,128.75) .. (150,132.75) .. controls (150,136.75) and (146.64,140) .. (142.5,140) .. controls (138.36,140) and (135,136.75) .. (135,132.75) -- cycle ; \draw (137.2,127.62) -- (147.8,137.88) ; \draw (147.8,127.62) -- (137.2,137.88) ; %Shape: Inductor [id:dp3454355331692156] \draw (35,155) -- (42.06,155) .. controls (43.68,155) and (45,156.12) .. (45,157.5) .. controls (45,158.88) and (43.68,160) .. (42.06,160) .. controls (43.68,160) and (45,161.12) .. (45,162.5) .. controls (45,163.88) and (43.68,165) .. (42.06,165) .. controls (43.68,165) and (45,166.12) .. (45,167.5) .. controls (45,168.88) and (43.68,170) .. (42.06,170) .. controls (43.68,170) and (45,171.12) .. (45,172.5) .. controls (45,173.88) and (43.68,175) .. (42.06,175) -- (35,175) ; %Straight Lines [id:da4690178114375858] \draw [dash pattern={on 0.84pt off 2.51pt}] (45,165.5) -- (130,185) -- (190,165) ; %Straight Lines [id:da10916309009890135] \draw [dash pattern={on 0.84pt off 2.51pt}] (45,164.5) -- (130,145) -- (190,165) ; % Text Node \draw (112,127) node [anchor=north west][inner sep=0.75pt] [align=left] {A}; % Text Node \draw (112,191) node [anchor=north west][inner sep=0.75pt] [align=left] {B}; \end{tikzpicture} $$

Задача о взвешенном выборе и случайной величине — В кресле препода №2

Объясняю на онлайн-семинаре с коллегами решение следующей задачи.

Пусть заданы n положительных чисел $$w_1$$, $$w_2$$, … $$w_n$$. Для каждого из них выберем значение $$x_i$$ случайной величины, равномерно распределенной на единичном интервале (0, 1). Существует ли функция $$f_w(x)$$, такая что максимальное значение этой функции $$\inline\max_{i=1,2,...n}\left\{f_{w_i}(x_i)\right\}$$ достигается на k-той выбранной паре $$(w_k, x_k)$$ с вероятностью, пропорциональной $$w_k$$?

Вместо более чем часового видео можете сразу прочитать решение без лишней воды.

Слушают и задают вопросы: Максим Федоров, Руслан Яруллин, Роман Попов, Михаил Чернявский.

Инструменты: Zoom, Sony Vegas Pro, Audacity, наушники Logitech, планшет Asus, самодельный стилус из предыдущего видео.

Экспонента

Смотрю лекции Алексея Савватеева по математике и получаю удовольствие. Вот лекция, в которой он переделал вузовский курс математики так, что его половина связана с изучением разных свойств экспоненты:

С 1:15:20 он строго доказывает формулу Эйлера о мнимой экспоненте $$e^{iy}=\sin y+i\cos y$$ тем же нестандартным методом, который я использовал в своей заметке про экспоненту и приближенные методы.

Круговая трактриса

Задача: по окружности небольшого радиуса едет трактор. К нему на жестком стержне прикреплен груз (например, прицеп). По какой траектории будет двигаться груз?

Всё зависит от длины стержня. Траектория может быть такой:

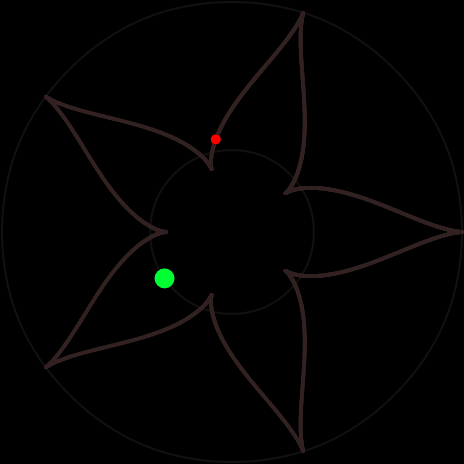
Смотрите в блоге о теоретической физике решение задачи и интерактивную анимацию ответа.

Чурофметика ★

Слушатели Эха Москвы помнят недавнее интервью Чурова, в котором он опровергает математику:

Чуров совершенно правильно назвал свою аналогию с конфетками наперсточничеством. Я собираюсь показать это, предложив адекватную аналогию.

Статистический анализ результатов выборов никакого отношения к нескольким конфеткам не имеет. Чтобы правильно показать его суть, нужно представить следующую ситуацию. Кто-то услышал гипотезу, по которой среди конфет эм-энд-эмс коричневые встречаются чаще. Он заподозрил известную торговую сеть в том, что они нагло вскрывают упаковки и досыпают коричневые конфеты, произведенные где-то в подвалах.

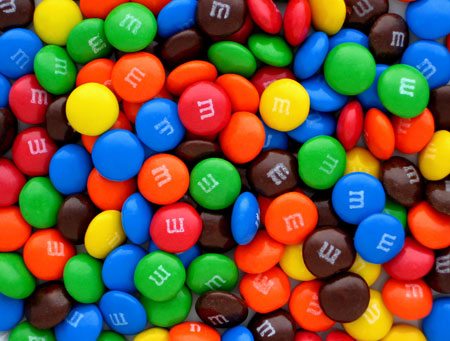
Наш герой отправляется в каждый магазин известной торговой сети и покупает несколько упаковок эм-энд-эмс. Перед тем как съесть очередную упаковку, он аккуратно записывает, сколько конфет каждого цвета в ней было. Герой объехал всю страну и начал анализировать числа.

Известно, что в одну упаковку в силу ограниченности объема можно поместить не больше 100 конфет. Но так как конфеты до упора никто не набивает, разумно ожидать, что в среднем (где-то больше, где-то меньше) в упаковках будет, скажем, 45 конфет. Для начала наш герой строит гистограмму, где по горизонтальной оси отложено общее количество конфет в упаковке, а по вертикальной — число встретившихся упаковок с данным количеством конфет. Он ожидает увидеть более-менее симметричную колоколообразную кривую с максимумом на 45 конфетах (более того, подобное исследование у конкурентов известной торговой сети показало именно такой результат).

Как же удивляется исследователь, обнаружив нечто совершенно неожиданное!

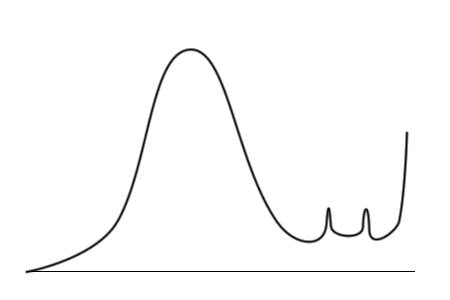
Здесь примечательны три вещи. Во-первых, кривая несимметрична: много упаковок с завышенным количеством конфет. Во-вторых, имеется большой пик в районе 100 конфет. В-третьих, встречаются небольшие пики в районе 80 и 90 конфет, которые можно объяснить только любовью фальсификаторов, подсыпающих конфеты, к круглым числам.

Тогда исследователь строит гистограммы, откладывая по вертикали не число упаковок, а уже общее число конфет разных цветов в упаковках с данным количеством конфет.

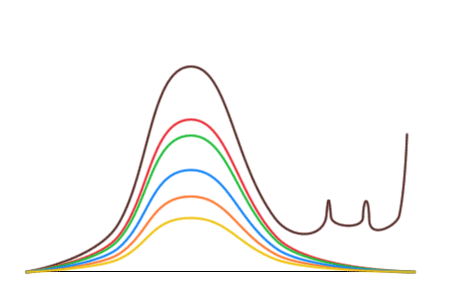
Оказывается, что безобразие действительно происходит только с коричневыми конфетами. Кривые для остальных конфет выглядят нормально и переходят друг в друга при растяжении или сжатии по вертикали. Их симметрия говорит о том, что конфеты ярких цветов в результате фальсификаций не изымаются. Таким образом, фальсификации заключаются только в преимущественном добавлении коричневых конфет.

Однако эти кривые позволяют сделать большее — сказать, сколько коричневых конфет было в упаковках до вброса! Так как левая половина коричневой кривой напоминает остальные, распределение которых не отличается от заводского, то можно растянуть красную кривую, чтобы левые половины красной и коричневой кривой совпали, и заменить искаженную правую часть.

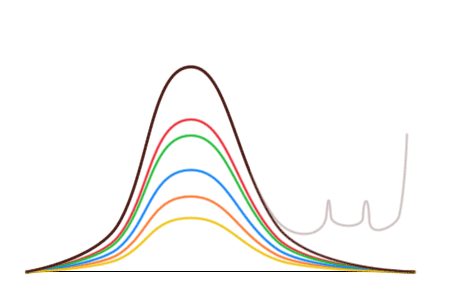
«Это прекрасно, но какое отношение имеют все эти конфеты к выборам и причем здесь Чуров?» — спросит нетерпеливый читатель. Если заменить конфеты разных цветов на проценты за ту или иную партию, а упаковки эм-энд-эмсов на избирательные участки, то наше конфетное расследование превратится в описание фальсификаций на выборах.

Подобный анализ проводился для выборов 2007 — 2009 годов и для последних думских выборов (идея несколько подробнее описана в первом материале). Анализ показывает, например, что на последних выборах Единая Россия получила не 49%, а 34%.

Вот такие, господин Чуров, конфетки!

Минус один в 28 степени

Из сегодняшнего Особого мнения:

Н.БОЛТЯНСКАЯ: «Правое дело» определилось с кандидатом в государственную думу: без Прохорова, но с теннисисткой Анной Чакветадзе. Как Вы считаете, дальнейший шансы «Правого дела»?

П.ГУСЕВ: Минус один в 28 степени.

Вообще-то всем известно, что (−1)²⁸ равно 1.

Рутина 2

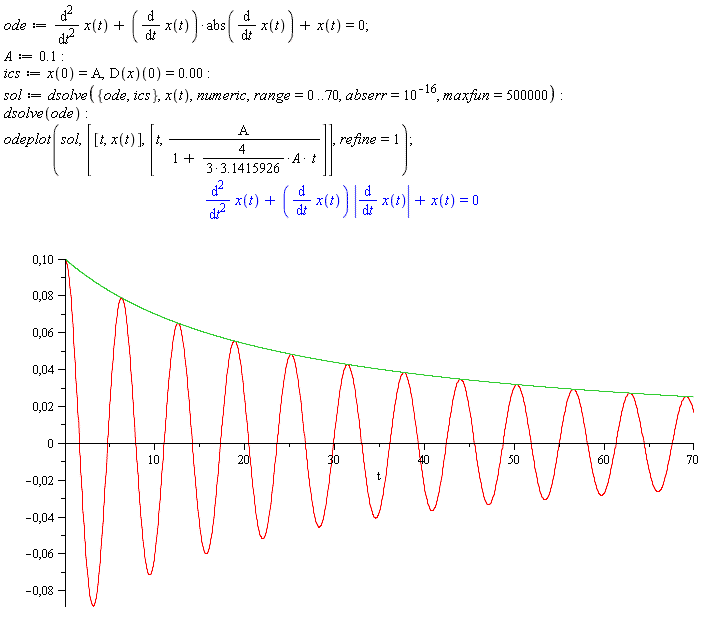
Оказывается, убывание амплитуды колебаний по гиперболическому закону — не такая бессмысленная вещь, как может показаться на первый взгляд. Примерно так убывает амплитуда малых колебаний, если сила трения пропорциональна квадрату скорости. Хотя на практике такая вещь, наверно, никогда не реализуется, но никто не запрещает исследовать решение модельного дифференциального уравнения.

Гуманитарии о биноме Ньютона

Интересно, это они сговорились, что ли? Раз:

Н. СВАНИДЗЕ — Я что мэр московский? Не моя работа, Сереж. Я же говорю с точки зрения здравого смысла.

С. БУНТМАН — Ну едешь ты в пробке, в метро, ты думаешь о том, с чего…

Н. СВАНИДЗЕ — Это не бином Ньютона. Есть великие города мира, в которых эти проблемы так или иначе решены, нужно посмотреть, как они действовали, приложить это к нашим реалиям. И начать. И все. Тут не нужно иметь сто пятьдесят пядей. Или сколько там надо пядей иметь во лбу.

Два:

При большом желании, это можно было бы сделать в рамках предварительного следствия. Но а уж в рамках возбужденного дела, с привлечением Интерпола и т.д. это совсем не выглядит Биномом Ньютона.

Но мы-то знаем, что бином Ньютона — это всего лишь процесс раскрытия скобок, для которого нужно знать лишь правила сложения и умножения.

Исследование на миллион

Задача о расположении прямых на плоскости была сформулирована В. И. Арнольдом в 1983 году. С тех пор эта нерешенная математическая проблема занимает лучшие умы человечества, подкупая простотой формулировки и создавая ощущение (в общем-то, ложное) близости решения.

Мы с Сергеем Белёвым и Денисом Уткиным рады сообщить о нашем скромном вкладе и представить отчет (PDF, 714 Кб) об упорных двухлетних исследованиях. В них использовались параллельные вычисления на десятках процессоров, некоторые сведения из теории группы кос и симметрической группы, а также факты из школьной геометрии и тригонометрии.

По понятным причинам в отчет включены только наиболее важные результаты. Тем не менее, он содержит изложение нескольких гениальных идей, проливающих свет на отдельные аспекты проблемы, существенно продвигающих ее понимание и даже позволяющих решить задачу в некоторых частных случаях.

Мы надеемся в ближайшем будущем полностью решить задачу и завершить наше исследование.

Рутина

Опять Вебпланета

Ага. Курсив мой.

Еще одним источником бесконечного количества комбинаций являются иррациональные числа. Например, число «е» бесконечно, и последовательность цифр на любом заранее выбранном его участке — неповторяющаяся. Таким образом, если взять любой сколь угодно большой набор цифр, то он должен содержаться в этом числе.

А то, что написано после слов «таким образом», в одно предложение не обосновывается. Это утверждение — вообще нерешенная математическая проблема.

Иногда нужно смотреть дальше Википедии.

Calc

Оказывается, что калькулятор Windows может считать факториалы от дробных чисел. При этом на самом деле вычисляется гамма-функция Эйлера. Например, «факториал» от −0,5 есть корень из числа пи.

Задача

На плоскости проведены n прямых, разбивающих ее на области. Они раскрашиваются в шахматном порядке: области, имеющие общие стороны, должны быть покрашены в разные цвета. Чему равна максимальная разность между числом черных и белых областей?

PS. Для заинтересовавшихся этой задачей приведу одну картинку для семи прямых:

Разность между числом черных и белых областей на этом рисунке — 7. Расположение прямых, дающее такую разность, не единственное, но вычисления на компьютере показали, что улучшить данный результат нельзя.

Лавинообразный клеточный автомат

Некоторое время назад я услышал описание следующей модели. Имеется «решетка» из квадратных ячеек. В каждой ячейке могут находиться частицы. На решетку случайным образом падают частицы. Если при добавлении новой частицы в ячейке становится 4 частицы, возникает неустойчивость, и эти 4 частицы переходят в соседние ячейки (соседями считаются ячейки, имеющие общие стороны). Если неустойчивая ячейка находится на границе решетки, то одна из частиц просто покидает структуру. Исследование «лавинообразных» процессов, когда в решетке скапливается достаточное количество частиц, представляет определенный интерес.

Данная система является (как и игра «Жизнь») клеточным автоматом. Такую систему легко запрограммировать. В ней могут возникать нетривиальные конструкции. Например, если сначала в каждую ячейку положить по 2 частицы, и потом добавлять частицы случайным образом, почти всегда возникают образования («генераторы»), испускающие «волны». А вот что получается, если сначала заполнить каждую ячейку четырьмя частицами и посмотреть, что останется, когда излишки «ссыпятся» через края:

Стоит усовершенствовать программу, нарисовавшую эту картинку, и исследовать данную модель подробнее.

Энциклопедия последовательностей целых чисел

Энциклопедия последовательностей целых чисел.

Как-то на спецкурсе по теории групп мы занимались уравнением классов. Когда надо было проверить результат работы программы, искавшей его решения, в этой энциклопедии была найдена зависимость числа решений от количества переменных.

О нуле в нулевой степени

Илья Бирман позволил, как мне сперва показалось, несколько вольное заявление о том, что 0⁰ = 1. Однако в ходе обмена мнениями выяснилось, что это не полушутливое, а вроде как серьезное мнение, от которого автор ни на шаг не отступит.

Как можно видеть в комментариях, не помогли мои объяснения того, откуда берется определение нулевой степени числа, разъяснения понятия «неопределенность» и «раскрытие неопределенности», а также другие соображения.

Его аргументация сводилась к тому, что это нужно «прочувствовать», а так же к нескольким примерам, в которых можно добиться несколько большего удобства в обозначениях, приняв, что 0⁰ = 1. Могу напомнить элементарные сведения из логики: сколь угодно много частных примеров не доказывают общее утверждение, а хотя бы один контрпример его опровергает.

Отвлекусь от тему и расскажу один случай. Пару дней назад нам на лекциях сказали про какую-то величину δ(m), которая равна 1, если m<0, и (-1)^m, если m>0. Мы принялись составлять формулы для величины δ(m), которые работали бы для любых m. Получилось вот что:

δ(m) = (-sign m)^m = (-1)^(m+|m|)/2

Вторая формула — моя. Видно, что в первой формуле при m=0 возникает неопределенность 0⁰. И можно заметить, что она будет работать, если положить 0⁰=1. Тогда я вспомнил Илью с его утверждением :)

Еще мысли об утверждении 0⁰=1:

1. По поводу ряда формул, упомянутых в этом комментарии. Следует понимать, что нет математических формул самих по себе. Каждая формула — по сути дела теорема, доказанная при определенных условиях. Например, формула Тейлора с остаточным членом в форме Лагранжа доказывается для значений x из проколотой окрестности x₀, то есть не совпадающих с x. При этом, разумеется, никаких 0⁰ не возникает.

2. Та полемика, которая разведена в комментариях, по объему и важности совсем не соответствует обсуждаемой проблеме. Лично я не буду ощущать никакой выгоды, считая, что 0⁰=1.

Математическая строгость и физики

Об отношении физиков к математическим строгостям очень хорошо написано во вступлении к книге «Квантовая механика и интегралы по траекториям» Р. Фейнмана и А. Хибса:

В книге Фейнмана и Хибса не дано строгого определения интеграла по траекториям; он вводится чисто интуитивно как предел соответствующего многократного интеграла (заметим, что введение комплексной единицы существенно усложняет строгое обоснование такого предельного перехода). Впрочем, для физика это в большинстве случаев не очень важно; ему нужна лишь уверенность, что строгое доказательство может быть получено.

Десять историй о математиках и физиках

Советую почитать Десять историй о математиках и физиках. Автор в популярной форме рассказывает о различиях между физикой и математикой, касается истории развития квантовой механики и доказательства теоремы Ферма, а так же рассматривает другие интересные вопросы.

Весьма познавательно, рекомендуется всем.